问在二维空间中寻找点的时间限制路径

EN

正如本征gives在评论中所指出的，这个问题有许多可能的解决方案，因此我将提出一种方法，根据您的路径所需的属性，提供合理的结果并允许灵活的自定义。

将问题分为两部分，首先在2D中找到一条路径，然后计算沿路径的距离，然后将速度和加速度与距离匹配的问题作为一维(加时)问题来解决。

对于路径，三次Bézier曲线似乎非常适合这个问题。三次Bézier曲线由4个控制点P0、P1、P2和P3定义。

P0和P3是曲线的起点和终点。P1和P2是控制点，用于指定起始点和终点处曲线的切线(分别由P0-P1和P2-P3线定义)。如果你沿着曲线飞行，那就是你在起点和终点移动的方向。

这里有一个交互式演示来了解控制点的位置对曲线的影响(三次Bézier是右边的蓝色曲线，有4个控制点)。

若要使用Bézier曲线定义飞行路径：

• 将P0设置为飞行路径的起点
• 将P3设置为端点
• 将P1设置为从P0开始速度矢量方向上的一个点
• 将P2设置为与P3的终点速度矢量相反的点

​

​

请注意，从P0到P1和从P2到P3的距离并不代表起始速度和结束速度的大小。相反，它们指定在曲线开始和结束时转弯的紧密性，以使曲线与开始和结束切线对齐。将控制点拉近以进行紧转，将其推到更远的地方进行更宽的转弯。然而，如果你想，你可以使转弯越大，所需的速度矢量是，更实际的物理。

如果你不想一直在转弯，你可以把这条路分割成几条Bézier曲线，或者Bézier曲线然后是一条直线然后是Bézier曲线，然后使切线与不同的部分相交。例如，您可能希望在飞行路径开始时采用一条弯曲的路径，然后在大部分的路径上沿着一条直线，在末端沿着一条弯曲的路径与所需的最终方向向量排列。这让你完全控制了你的飞行路线。

该解易于推广到三维。

现在您有了一条路径，您需要弄清楚如何沿着曲线加速和减速，以便在正确的时间和速度到达目的地。首先，计算沿曲线的距离：

Bézier曲线的弧长

如果您知道开始时间、结束时间以及开始和结束速度(起始速度和结束速度向量的大小)，您可以计算出在起始时间和结束时间之间沿曲线飞行的距离，假设您在旅途中从起始速度直线加速到终点速度(距离是直线下的区域)：

​

​

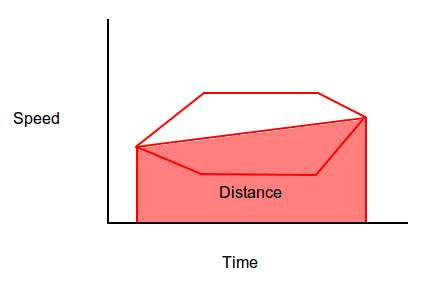
由于该区域很可能与Bézier曲线沿线的计算距离不同，因此需要创建一个分段函数，该函数在起始时间和结束时间之间的直线下具有所需的区域。该图像显示了两个这样的函数，用于处理旅行距离大于预期的情况，并且通过减速、恒速再加速来减小面积，反之亦然。这些例子显示了加速度的瞬时变化，而不是速度的变化。您可以选择任何您喜欢的函数，只要开始和结束时间的开始和结束速度与所需的值匹配，并且函数下的区域等于沿着路径的距离。