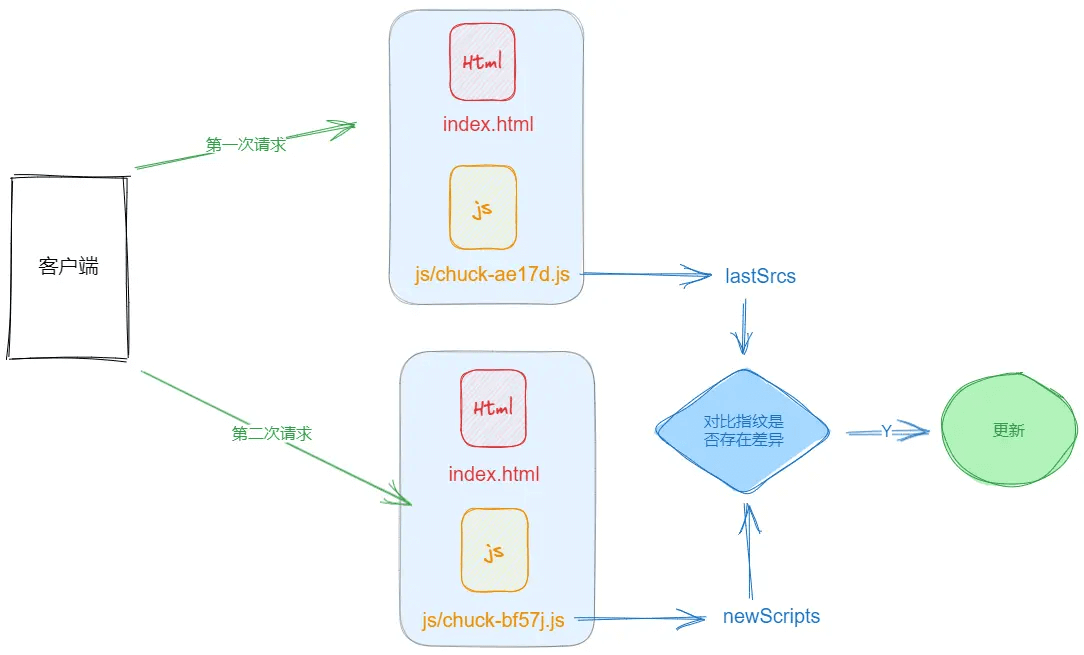
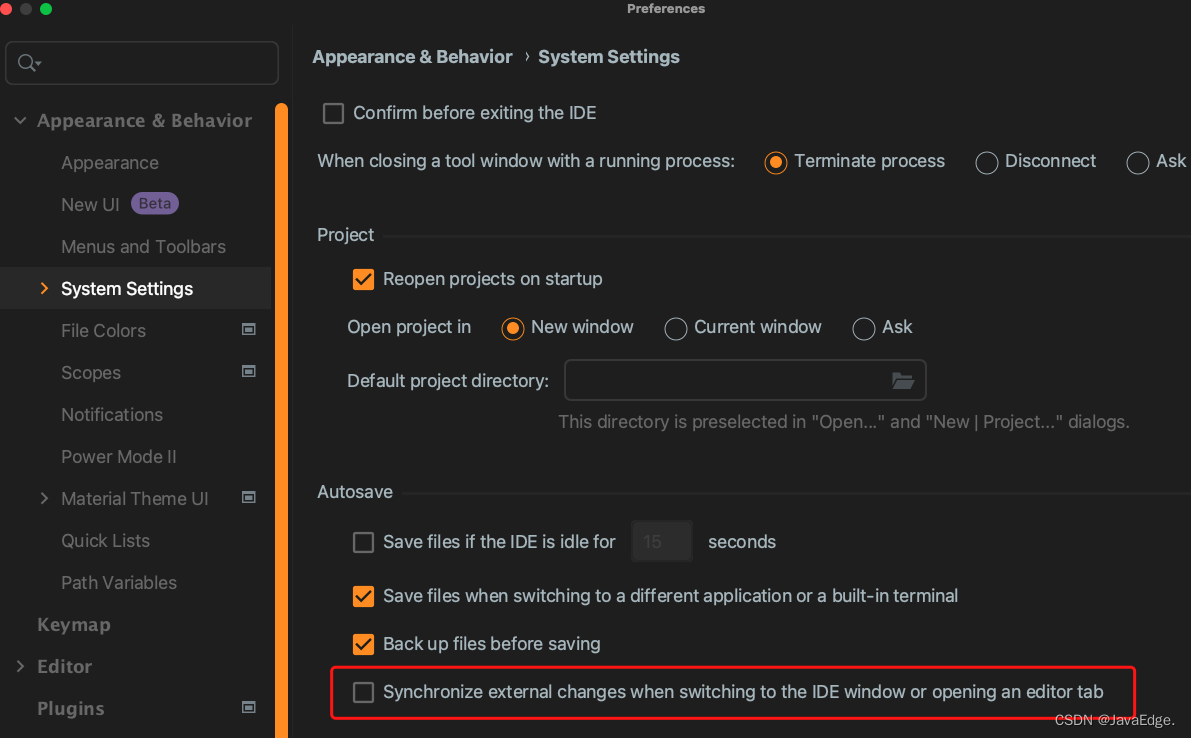
我有以下几点:
type Name = String
data Prop
= Var Name
| F
| T
| Not Prop
| Prop :|: Prop
| Prop :&: Prop
deriving (Eq, Read)
infixr 2 :|:类型Prop表示一个命题公式。命题变量如p和q可以用Var "p“和Var "q”表示。
F和T是假和真的常量布尔值。
不表示否定(~或)
::和:&:表示分离(/)和合并(/)
我们可以写逻辑命题:
( Var "p" :|: Var "q") :&: ( Not (Var "p") :&: Var "q")我必须做的是:通过使Prop成为类Show的一个实例来替换Not,:如下所示:和:&:with ~,/和/\,以便下列内容为真:
test_ShowProp :: Bool
test_ShowProp =
show (Not (Var "P") :&: Var "Q") == "((~P)/\Q)"到目前为止,这就是我的实现:
instance Show Prop where
show (Var p) = p
show (Not (Var p)) = "(~" ++ p ++ ")"
show (Var p :|: Var q) = p ++ "\\/" ++ q
show (Var p :&: Var q) = p ++ "/\\" ++ q但这并不能涵盖所有的案件,只是一些基本的案例。我应该如何继续实现,以便它处理任何命题公式,而不仅仅是硬编码公式?因为目前
(Var "p" :&: Var "q")产出: p/\q
但
Not (Var "p" :&: Var "q")输出:功能显示中的非详尽的模式
回答 2
Stack Overflow用户
回答已采纳
发布于 2019-01-04 14:16:13
您应该只匹配公式的一个“层”,即只匹配一个构造函数,并利用递归对子公式进行攻击。例如,
show (Not f) = "(~" ++ show f ++ ")"将适用于任何以否定开始的公式,即使在该否定下有一个非变量的子公式。
正确的括号可能会很棘手。您需要慷慨地使用括号或定义showsPrec。如果你是一个初学者,我建议前者,这不需要应付优先级别。
Stack Overflow用户
发布于 2019-01-04 14:15:41
您希望在定义中递归地调用show。所以使用Not的例子应该是
show (Not p) = "(~" ++ show p ++ ")"页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/54046804
复制