爬楼梯问题（4种解法）

70. 爬楼梯

提示

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

• 1 <= n <= 45

以上是一个爬楼梯问题，我们通过找规律来解决问题。

楼顶数：1 2 3 4 5 6

方法数：1 2 3 5 8 13

通过观察发现楼顶数x与方法数F( x )的关系为

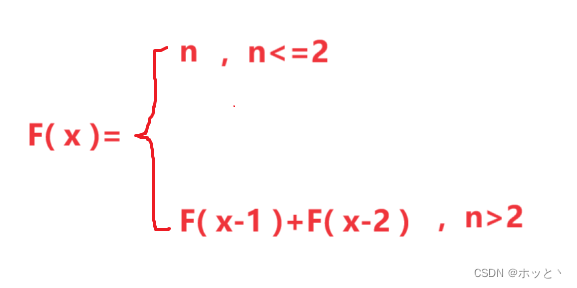
出现这样一个递推公式我们第一想到的就是递归来实现。接下来先从递归讲起。

1.递归

int F(int n)
{
    if(n<=2)
        return n;
    else
        return F(n-1)+F(n-2);
}

递归是这样理解把它拆分出来，两个字，递和归 递：递推（这就需要找到递推公式） 归：回归（需要找到回归条件，递推过程逐渐逼近回归条件）

下面对以上代码进行剖析：

红线为递推过程，绿线为回归过程。

接下来是复杂度分析

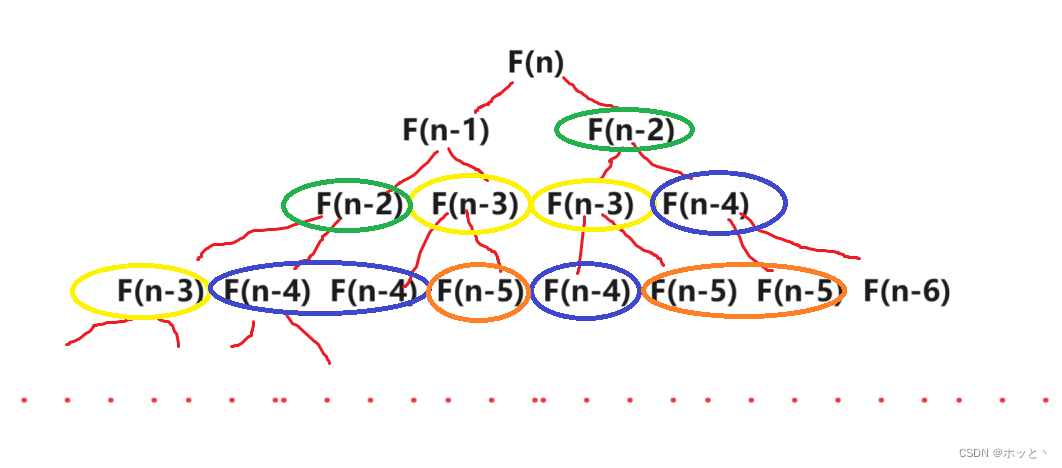
时间复杂度为O(2^n)，空间复杂度O(n)

通过观察我们发现出现很多重复计算的地方（图中画圈的地方）。为了解决这个问题，我们想象一下，把每次计算的数据存起来，下次用到的时候就不用计算，直接返回。而以下的记忆递归就可以解决这个问题。

2.记忆递归

int arr[46]={0};
F(int n)
{
    if(n<=2)
        return n;
    if(arr[n]!=0)
        return arr[n];
    else
        return arr[n]=F(n-1)+F(n-2);
}

创建一个数组赋初始值为零，把每次返回的值存给这个数组，这样可以避免重复计算，判断a[n]为非0则直接返回。时间复杂度为O(n),空间复杂度为O(n)。

3.动态规划

int F(int n){
    int arr[46]={0};
    arr[1]=1,arr[2]=2;
    for(int i=3;i<n+1;i++)
    {
        arr[i]=arr[i-1]+arr[i-2];
    }
    return arr[n];
}

把1到n，每个楼顶对应的方法数存入数组中，用前两个来计算后一个，直到推到n，此方法相比以上方法，减少了递归带来的内存申请，时间复杂度为O(n)，空间复杂度为O(1)。

4.滚动数组

int F(int n) {
    int a = 0, b = 0, r = 1;
    for (int i = 1; i <= n; ++i) {
        a = b;
        b = r;
        r = a + b;
    }
    return r;
}

此方法比前几种更为简洁，用三个数来回滚动来实现，时间复杂度为O(n)，空间复杂度为O(1)。