KD-Tree算法从原理到实践解析

1. 概述

KD-Tree，全称 K-Dimensional Tree，是一种用于组织 K 维空间中点数据的数据结构，它是二叉搜索树（BST） 在多维空间上的扩展，也叫“二叉”空间分割树，无论维度 K 是多少，KD-Tree 的每个节点都只有左和右两个子树。

核心思想：通过交替地使用不同的维度作为分割轴，递归地将 K 维空间划分为若干个更小的区域，从而高效地进行范围搜索和最近邻搜索，用于任意维度 K 的最近邻搜索和范围搜索，尤其在中低维（K<20）表现优异。

类比：你可以把它想象成一个在多维空间下不断“切蛋糕”的过程，比如在 2D 空间下，首先垂直切一刀，然后水平切一刀，然后再垂直切……如此反复，将空间划分为许多矩形区域。

2. 原理与构建

2.1 数据结构

树中的每个节点代表一个 K 维点，并包含以下信息： 数据点：该节点所代表的 K 维坐标。 分割维度：当前节点是根据哪个维度进行分割的（例如，0 代表 x 轴，1 代表 y 轴）。 左子树：包含所有在当前分割维度上值小于该节点值的点。 右子树：包含所有在当前分割维度上值大于或等于该节点值的点。

2.2 算法原理

• 分割方式：在构建树的每一层，KD-Tree 只选用一个特定的维度（比如第 i 维）来进行分割，它用一个垂直于该维度坐标轴的超平面将整个空间一分为二。
• 判断规则：对于空间中的任何一个点，判断它属于左子树还是右子树的规则非常简单：
• 左子树：该点在第 i 维上的坐标值 小于 当前节点的第 i 维坐标值。
• 右子树：该点在第 i 维上的坐标值 大于或等于 当前节点的第 i 维坐标值。

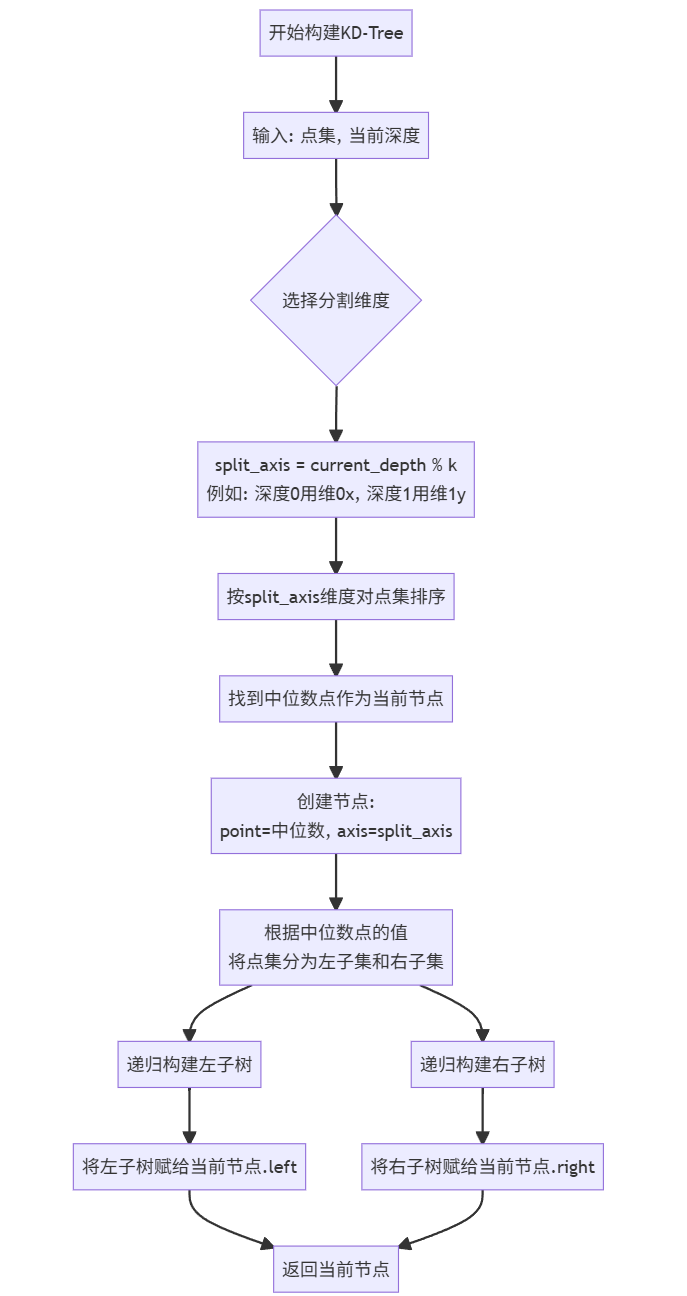
2.3 构建算法示例

（以 2D 为例，点集：[(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)]） 构建一个高效的 KD-Tree 的关键在于如何选择分割维度和分割点。常见的方法是：

分割维度的选择：循环交替地使用各个维度，例如，根节点用第 0 维（x轴），下一层用第 1 维（y轴），再下一层又用回第 0 维，以此类推。

分割点的选择：通常选择当前维度下所有点的中位数作为分割点，可以保证构建出来的树是平衡的，搜索效率最高。

构建步骤示例：

• a. 根节点 (深度=0， 使用 x 维)： 所有点： (2,3), (5,4), (9,6), (4,7), (8,1), (7,2) 按 x 坐标排序： (2,3), (4,7), (5,4), (7,2), (8,1), (9,6) 中位数是 (7,2) （如果偶数个点，通常取中间偏右或偏左均可，这里取 (7,2)）。 根节点 = (7,2)。分割维度为 x。 左子树（x < 7）： (2,3), (5,4), (4,7), (9,6) -> 实际上应为 (2,3), (4,7), (5,4) （(9,6)的x是9>7，应归右子树，这里原集合描述可能有误，修正后左子树点为 (2,3), (4,7), (5,4)） 右子树（x >= 7）： (8,1), (9,6)
• b. 根节点的左子树 (深度=1， 使用 y 维)： 点集： (2,3), (4,7), (5,4) 按 y 坐标排序： (2,3), (5,4), (4,7) 中位数是 (5,4)。 节点 = (5,4)，分割维度为 y。 左子树（y < 4）： (2,3) 右子树（y >= 4）： (4,7)
• c. 根节点的右子树 (深度=1， 使用 y 维)： 点集： (8,1), (9,6) 按 y 坐标排序： (8,1), (9,6) 中位数： 取 (9,6) （规则之一，取中间偏右）。 节点 = (9,6)。分割维度为 y。 左子树（y < 6）： (8,1) 右子树（y >= 6）： None
• 继续递归地为每个子树执行上述过程，直到所有点都被插入。
• 最终构建出的 KD-Tree 结构如下图所示（基于修正后的点集）：

               (7, 2)
                  |
        ----------------------
        |                    |
      (5, 4)               (9, 6)
        |                    |
   -----------           -----------
   |         |           |         |
 (2, 3)    (4, 7)      (8, 1)     None

3. 最近邻搜索（NN Search）算法

这是 KD-Tree 最经典的应用，算法比构建要复杂，它是一种优化后的深度优先搜索，核心是剪枝。

算法步骤：

从根节点开始，递归地向下搜索，就像在二叉搜索树中查找一样，根据当前节点的分割维度，决定是进入左子树还是右子树，这条路径上的叶子节点就是当前的“最近邻”候选点。

回溯 ：

在回溯过程中，每到一个节点，都做以下事情：

• 1. 检查当前节点是否比已知的最近邻更近，如果是，则更新最近邻。
• • 如果否，说明另一侧子树不可能有更近的点，可以跳过（剪枝），继续回溯。
  • 如果是，说明另一侧子树有可能存在更近的点，必须递归地搜索另一侧子树。
  1. 检查另一侧子树是否可能包含更近的点（剪枝判断）。判断的依据是：目标点到当前节点分割超平面的距离是否小于到当前最近邻点的距离。

3.1 K=2示例

import numpy as np
from scipy.spatial import KDTree
# 1. 创建示例数据：一组二维点
points = np.array([[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]])
print("Data points:")
print(points)
# 2. 构建 KD-Tree
tree = KDTree(points)
print("\nKD-Tree 构建完成")
# 3. 定义一个目标查询点
query_point = np.array([3, 4.5])
print(f"\n目标查询点: {query_point}")
# 4. 查询最近邻
distance, index = tree.query(query_point, k=1) # k=1 表示找最近的1个邻居
nearest_point = points[index]
print(f"\n最邻近索引: {index}")
print(f"最邻近节点: {nearest_point}")
print(f"距离: {distance:.4f}")
# 5. 查询 K=2 个最近邻
distances, indices = tree.query(query_point, k=2)
print(f"\n两个最邻近索引: {indices}")
print(f"最邻近节点:\n{points[indices]}")
print(f"距离: {distances}")
# 6. 范围查询：查找以query_point为中心，半径为2.0的圆内的点
indices_in_range = tree.query_ball_point(query_point, r=2.0) 
print(f"\n {query_point}半径 2.0 以内点索引: {indices_in_range}")
print(f"坐标:\n{points[indices_in_range]}")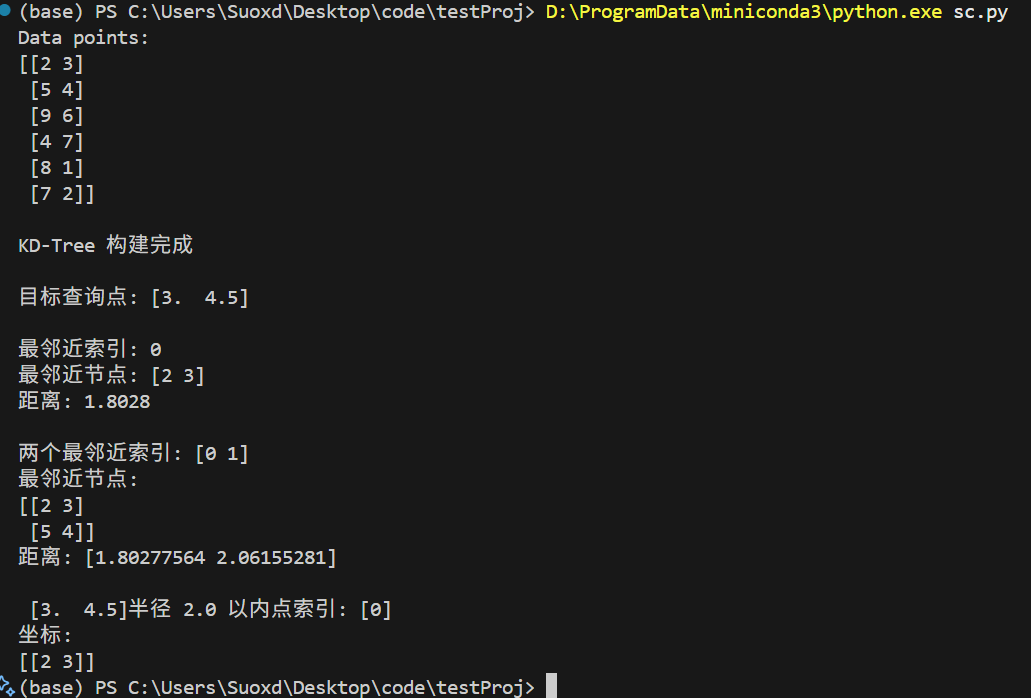

在这里插入图片描述

3.1 K=3示例

import numpy as np
from scipy.spatial import KDTree
# 1. 创建3维示例数据
```python
points_3d = np.array([
    [2, 3, 1],
    [5, 4, 7],
    [9, 6, 8],
    [4, 7, 5],
    [8, 1, 3],
    [7, 2, 9]
])
print("Data points:")
print(points_3d)
# 2. 构建3D-Tree
tree_3d = KDTree(points_3d)
# 3. 定义一个3维目标查询点
query_point_3d = np.array([3, 4, 5])
print(f"\n待查询点: {query_point_3d}")
# 4. 查询最近邻
distance_3d, index_3d = tree_3d.query(query_point_3d, k=1)
nearest_point_3d = points_3d[index_3d]
print(f"\n最邻近点索引: {index_3d}")
print(f"点坐标: {nearest_point_3d}")
print(f"距离: {distance_3d:.4f}")
# 5. 手动计算所有距离以验证
print("\n手动计算距离 (3,4,5):")
for i, point in enumerate(points_3d):
    dist = np.sqrt(np.sum((point - query_point_3d) ** 2))
    print(f"To {point}: {dist:.4f} (index {i})")

在这里插入图片描述