【算法基础篇】（五十二）组合计数实战宝典：7 道经典例题带你吃透排列组合核心玩法

前言

组合计数是组合数学的 “实战核心”，它不像基础概念那样抽象，而是直接对应算法竞赛和实际应用中的各类计数问题 —— 小到给兔子编号、安排牛的位置，大到齿轮组损耗计算、网格三角形计数，本质上都是组合计数的灵活运用。 很多同学学完排列组合的公式后，一碰到具体题目就卡壳，核心原因是没掌握 “问题转化” 的思维：如何把实际问题抽象成组合模型，如何选择合适的计数方法（加法原理、乘法原理、组合数、正难则反等）。 本文将围绕 7 道经典组合计数题目展开，每道题都来自洛谷等权威平台，覆盖从入门到进阶的难度梯度。我们会从题目分析入手，拆解问题本质，推导解题思路，最后给出完整的 C++ 代码和细节注释。无论你是算法新手，还是想巩固组合计数的进阶选手，跟着这篇文章一步步走，都能收获满满！

一、组合计数基础回顾（解题必备）

在开始做题前，先快速回顾几个核心知识点，这些是解题的 “万能钥匙”：

1. 加法原理：分类计数，各类方案互不干扰，总方案数为各类方案数之和。
2. 乘法原理：分步计数，各步骤缺一不可，总方案数为各步骤方案数之积。
3. 组合数：从 n 个不同元素中选 m 个（不考虑顺序），记为

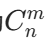
​，公式为

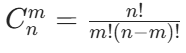
（核心性质：

）。

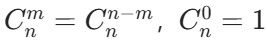
1. 正难则反：当直接计数困难时，可先算总方案数，再减去不符合条件的方案数（如 “越狱问题”“数三角形问题”）。
2. 乘法逆元：用于模运算中的除法转换，当 p 为质数时，a 的逆元为

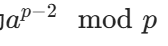
（费马小定理），是组合数取模的关键。

这些知识点看似简单，但要灵活运用到题目中，需要通过具体场景反复锤炼。下面我们逐个攻克 7 道经典题！

二、经典题目实战解析（含 C++ 代码）

题目 1：编号（洛谷 P1866）—— 排序 + 乘法原理，入门必刷

题目链接：https://www.luogu.com.cn/problem/P1866

题目描述

太郎有 N 只兔子，每只兔子 i 想要一个 1 到Mi​之间的整数作为编号（可等于 1 或Mi​），且所有兔子的编号必须不同。求合法的编号方案数，答案对10^{9}+7取模；若不可能则输出 0。

输入示例

2
5 8

输出示例

35

题目分析

这道题的核心矛盾是 “编号不重复” 和 “每只兔子的编号有范围限制”。直接暴力枚举显然不现实，需要找到一种有序的计数方式。

关键思路：排序后分步计数。

• 先将所有兔子的Mi​从小到大排序。为什么要排序？因为编号是不重复的正整数，第 i 只兔子（排序后）能选择的编号数量，取决于它的Mi​和前面已经选了的编号个数。
• 排序后，第 i 只兔子（从 1 开始计数）前面已经选了 i-1 个不同的编号，所以它能选择的编号数量为Mi​−(i−1)（因为编号必须≤Mi​，且不能和前面的 i-1 个重复）。
• 若某只兔子的Mi​−(i−1)≤0，说明没有合法编号可选，直接输出 0。
• 总方案数为所有兔子可选编号数的乘积（乘法原理，分步选择，每一步的选择数相乘）。

逻辑推导

以示例输入为例：

• N=2，M=[5,8]，排序后为[5,8]。
• 第 1 只兔子：前面选了 0 个编号，可选数量为 5-0=5（编号 1-5）。
• 第 2 只兔子：前面选了 1 个编号，可选数量为 8-1=7（不能选前面选的那个，剩下 7 个）。
• 总方案数：5×7=35，和示例输出一致。

C++ 代码实现

#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;
const int N = 55;
const int MOD = 1e9 + 7;

int main() {
    int n;
    cin >> n;
    int m[N];
    for (int i = 1; i <= n; ++i) {
        cin >> m[i];
    }
    // 排序是关键，保证后续分步计数的合理性
    sort(m + 1, m + 1 + n);
    
    LL result = 1;
    for (int i = 1; i <= n; ++i) {
        // 第i只兔子可选的编号数 = M_i - (i-1)
        m[i] -= (i - 1);
        if (m[i] <= 0) {
            // 没有合法编号，直接输出0
            cout << 0 << endl;
            return 0;
        }
        // 乘法原理，累乘结果并取模
        result = result * m[i] % MOD;
    }
    cout << result << endl;
    return 0;
}

代码注释

• 排序：将Mi​从小到大排序，确保每一步的可选编号数计算正确。
• 分步计数：第 i 只兔子的可选数量为Mi​−(i−1)，若为负数则无解。
• 取模：由于结果可能很大，每一步乘法后都对109+7取模，避免溢出。

难度总结

★ 入门级，核心考察 “排序 + 乘法原理” 的结合，学会将无序问题转化为有序问题，是组合计数的基础思维。

题目 2：文的数学游戏（洛谷 P8469）—— 最大公约数 + 乘法原理

题目链接：https://www.luogu.com.cn/problem/P8469

题目描述

给定长度为 n 的整数序列 a，构造长度为 n 的序列 b，满足 1≤bi​≤ai​（1≤i≤n），且gcd(b1​,b2​,...,bn​)（最大公约数）最大。求这个最大的 gcd 值，以及对应的合法序列 b 的个数（对109+7取模）。

输入示例

3
1 2 3

输出示例

1 6

题目分析

这道题有两个目标：一是找到最大的 gcd，二是计算对应的方案数。核心是理解 “gcd 最大” 的含义。

关键思路：最大 gcd 是序列 a 的最小值。

• 假设最大 gcd 为 d，那么所有bi​都必须是 d 的倍数（因为 gcd 是 d，所有元素都能被 d 整除）。
• 要使 d 最大，d 不能超过任何一个bi​的最大值，而bi​≤ai​，所以 d 最大只能是ai​中的最小值（记为 min_a）。因为如果 d>min_a，那么bi​中至少有一个（对应 a_i=min_a 的那个）无法是 d 的倍数（因为bi​≤min_a <<d），矛盾。
• 方案数计算：对于每个ai​，bi​必须是 d 的倍数且≤ai​，所以可选的bi​数量为

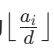
。总方案数为所有

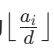
的乘积（乘法原理）。

逻辑推导

以示例输入为例：

• a=[1,2,3]，min_a=1，所以最大 gcd=1。
• 第 1 只兔子：⌊1/1⌋=1（可选 1）。
• 第 2 只兔子：⌊2/1⌋=2（可选 1,2）。
• 第 3 只兔子：⌊3/1⌋=3（可选 1,2,3）。
• 总方案数：1×2×3=6，和示例输出一致。

C++ 代码实现

#include <iostream>
#include <climits> // 用于INT_MAX
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
const int MOD = 1e9 + 7;

int main() {
    int n;
    cin >> n;
    int a[N];
    int min_a = INT_MAX; // 初始化最小a_i为无穷大
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        if (a[i] < min_a) {
            min_a = a[i]; // 找到a数组的最小值
        }
    }
    
    LL count = 1;
    for (int i = 1; i <= n; ++i) {
        // 每个a_i对应的可选b_i数量：a_i / min_a
        count = count * (a[i] / min_a) % MOD;
    }
    
    cout << min_a << " " << count << endl;
    return 0;
}

代码注释

• 找最小 a_i：遍历数组找到 min_a，即最大可能的 gcd。
• 计算方案数：对于每个 a_i，计算

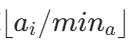
，累乘取模。

• 时间复杂度：O (n)，适合 n≤1e5 的范围。

难度总结

★ 入门级，核心考察 “最大公约数的性质” 和 “乘法原理”，需要理解 “gcd 最大” 的约束条件如何转化为具体的数值（数组最小值）。

题目 3：Bulls And Cows（洛谷 P6191）—— 组合数求和，灵活运用组合模型

题目链接：https://www.luogu.com.cn/problem/P6191

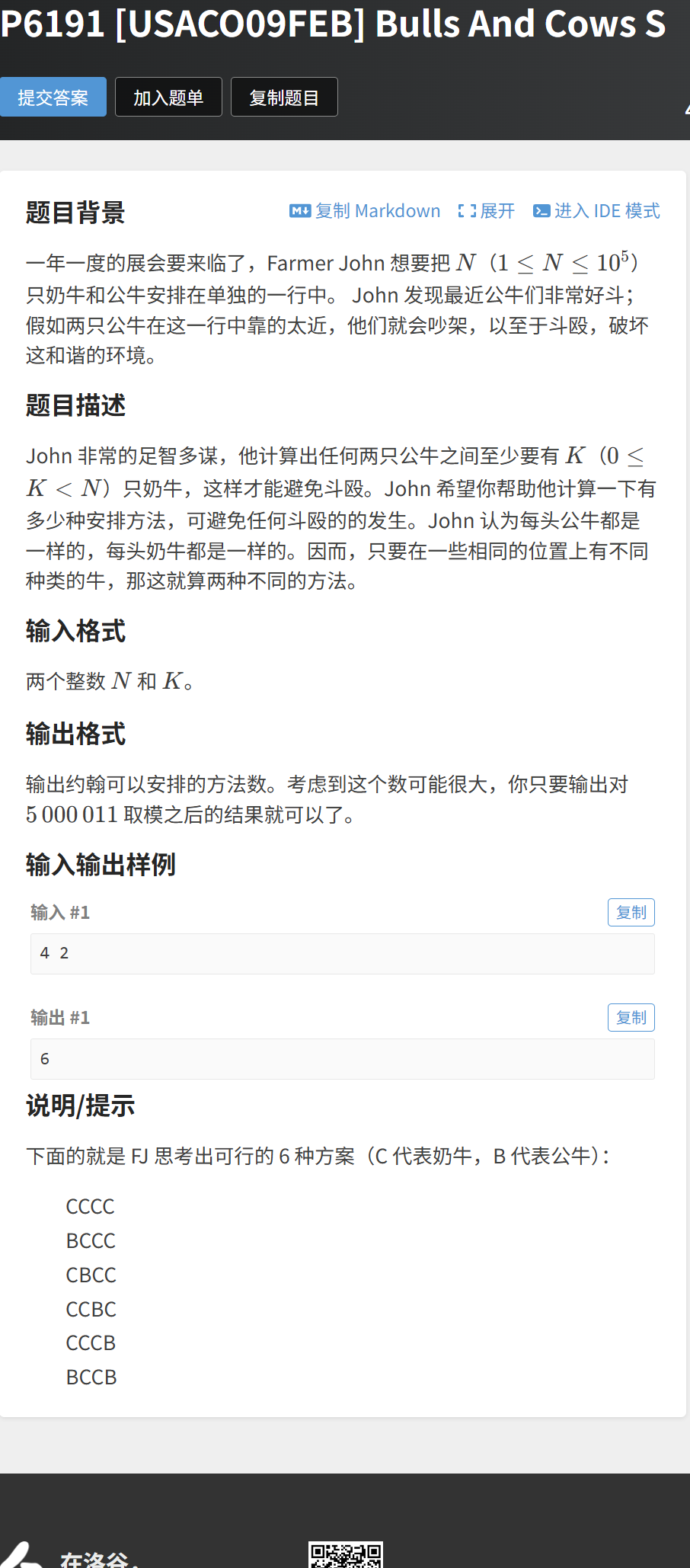
题目描述

John 有 N 个位置，要安排公牛和奶牛，要求任意两只公牛之间至少有 K 只奶牛。公牛和奶牛都是相同的，求合法的安排方案数（对 5000011 取模）。

输入示例

4 2

输出示例

6

题目分析

这道题的关键是 “相同元素的排列 + 约束条件（公牛之间至少 K 只奶牛）”。由于元素相同，我们只需要计算 “放多少只公牛” 以及 “放在哪里”。

关键思路：枚举公牛数量，转化为组合数问题。

• 设放 i 只公牛（i≥0），计算每种 i 对应的方案数，最后求和（加法原理）。
• 当 i=0 时：只有 1 种方案（全是奶牛）。
• 当 i=1 时：公牛可以放在任意 N 个位置，方案数为

​。

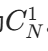
• 当 i≥2 时：约束条件是 “每两只公牛之间至少 K 只奶牛”。如何转化为组合数？
  • 先 “预留” 奶牛位置：i 只公牛之间需要 i-1 个间隔，每个间隔至少 K 只奶牛，共需要预留(i−1)×K只奶牛的位置。
  • 剩下的可用位置数：N−(i−1)×K（总位置数减去预留的奶牛位置数）。
  • 现在问题转化为：在剩下的N−(i−1)×K个位置中，选 i 个位置放公牛（奶牛自然填充剩下的位置），方案数为

  

  。

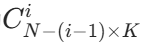
• 终止条件：当N−(i−1)×K<i时，无法放下 i 只公牛，停止枚举。

逻辑推导

以示例输入为例（N=4，K=2）：

• i=0：方案数 1。
• i=1：

。

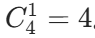
• i=2：预留(2−1)×2=2个奶牛位置，剩下 4-2=2 个位置，选 2 个放公牛：

。

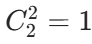
• i=3：预留(3−1)×2=4个位置，剩下 4-4=0 个位置，

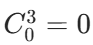
，停止枚举。

• 总方案数：1+4+1=6，和示例输出一致。

C++ 代码实现

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
const int MOD = 5000011;

LL f[N]; // 阶乘数组：f[i] = i! mod MOD
LL g[N]; // 阶乘逆元数组：g[i] = (i!)^{-1} mod MOD

// 快速幂：计算a^b mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    while (b) {
        if (b & 1) ret = ret * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

// 初始化阶乘和逆元数组
void init(int max_n) {
    f[0] = 1;
    for (int i = 1; i <= max_n; ++i) {
        f[i] = i * f[i - 1] % MOD;
    }
    // 费马小定理求逆元
    g[max_n] = qpow(f[max_n], MOD - 2, MOD);
    for (int i = max_n - 1; i >= 0; --i) {
        g[i] = (i + 1) * g[i + 1] % MOD;
    }
}

// 计算组合数C(n, m) mod MOD
LL C(int n, int m) {
    if (n < m) return 0; // 不可能的情况，返回0
    return f[n] * g[m] % MOD * g[n - m] % MOD;
}

int main() {
    int n, k;
    cin >> n >> k;
    init(n); // 初始化阶乘数组，最大需要n!
    
    LL result = 1; // i=0时的方案数
    for (int i = 1; ; ++i) {
        // 计算可用位置数：n - (i-1)*k
        int available = n - (i - 1) * k;
        if (available < i) break; // 无法放下i只公牛，终止
        // 累加i只公牛的方案数
        result = (result + C(available, i)) % MOD;
    }
    cout << result << endl;
    return 0;
}

代码注释

• 快速幂 + 逆元：由于需要计算组合数取模，用费马小定理求阶乘的逆元。
• 组合数计算：

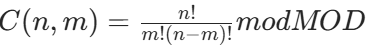
，通过预存阶乘和逆元数组，实现 O (1) 查询。

• 枚举公牛数量：从 i=1 开始枚举，直到可用位置数小于 i，累加所有合法方案数。

难度总结

★ 基础级，核心考察 “约束条件转化为组合模型”，学会 “预留位置” 的技巧，将有约束的计数问题转化为无约束的组合数问题。

题目 4：炼金术（洛谷 P8557）—— 幂运算，分步计数的极致简化

题目链接：https://www.luogu.com.cn/problem/P8557

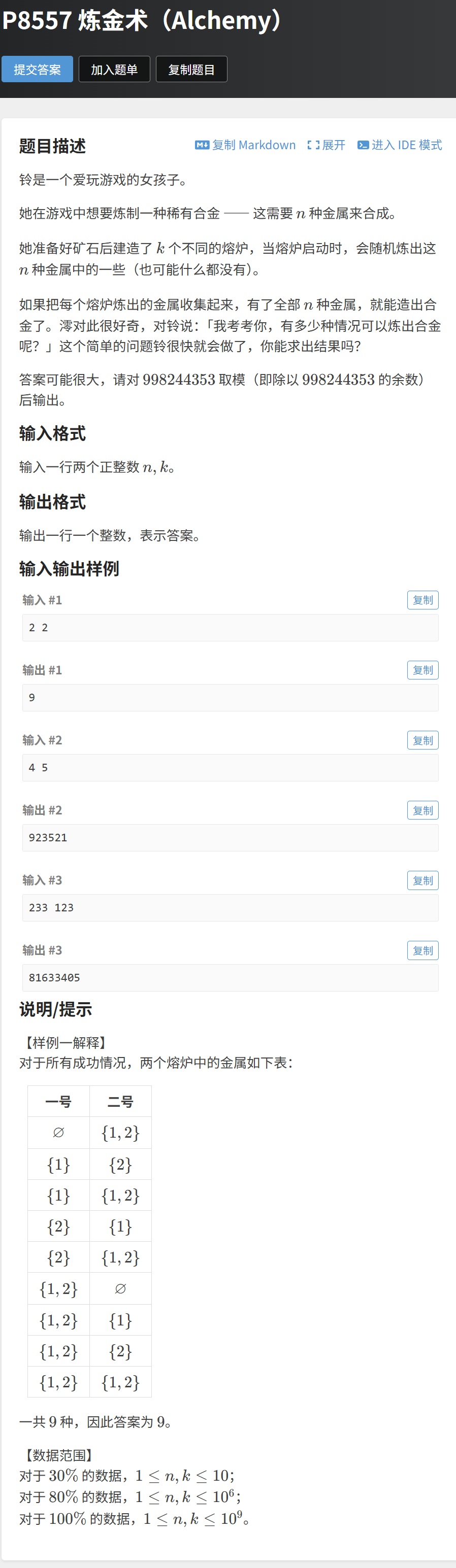
题目描述

铃要炼制一种合金，需要 n 种金属。她有 k 个不同的熔炉，每个熔炉启动时会随机炼出若干种金属（可能没有）。收集所有熔炉炼出的金属，若包含全部 n 种金属，则算一种成功情况。求成功的情况数（对 998244353 取模）。

输入示例

2 2

输出示例

9

题目分析

这道题的关键是 “每个熔炉的选择独立” 和 “最终覆盖所有 n 种金属”。直接计算 “覆盖所有金属” 的情况数较难，可转化为 “每种金属至少被一个熔炉炼出”。

关键思路：分步计数 + 幂运算。

• 对于每种金属，考虑它被多少个熔炉炼出：每个熔炉有两种选择 —— 炼出该金属或不炼出，共2k种情况。
• 但要满足 “至少被一个熔炉炼出”，所以每种金属的有效情况数为

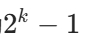
（减去 “所有熔炉都不炼出该金属” 的情况）。

• 由于 n 种金属的情况是独立的（一种金属的炼出情况不影响另一种），总成功情况数为

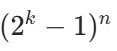
（乘法原理，n 个(2k−1)相乘）。

逻辑推导

以示例输入为例（n=2，k=2）：

• 每种金属的有效情况数：

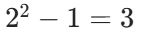
（熔炉 1 炼出、熔炉 2 炼出、两个都炼出）。

• 总情况数：3×3=9，和示例输出一致。

C++ 代码实现

#include <iostream>
using namespace std;

typedef long long LL;
const int MOD = 998244353;

// 快速幂：计算a^b mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    while (b) {
        if (b & 1) ret = ret * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

int main() {
    LL n, k;
    cin >> n >> k;
    // 计算2^k mod MOD
    LL pow2 = qpow(2, k, MOD);
    // 每种金属的有效情况数：pow2 - 1
    LL per_metal = (pow2 - 1 + MOD) % MOD; // +MOD避免负数
    // 总情况数：(per_metal)^n mod MOD
    LL result = qpow(per_metal, n, MOD);
    cout << result << endl;
    return 0;
}

代码注释

• 快速幂：高效计算

和

，时间复杂度 O (logk + logn)，适合 k 和 n 较大的情况。

• 防负数：由于 pow2 可能为 0（当 k=0 时），pow2-1 可能为负数，所以加 MOD 后再取模。

难度总结

★ 入门级，核心考察 “独立事件的分步计数”，学会将复杂的覆盖问题转化为单个元素的独立计数，再用幂运算快速求解。

题目 5：越狱（洛谷 P3197）—— 正难则反，经典计数技巧

题目链接：https://www.luogu.com.cn/problem/P3197

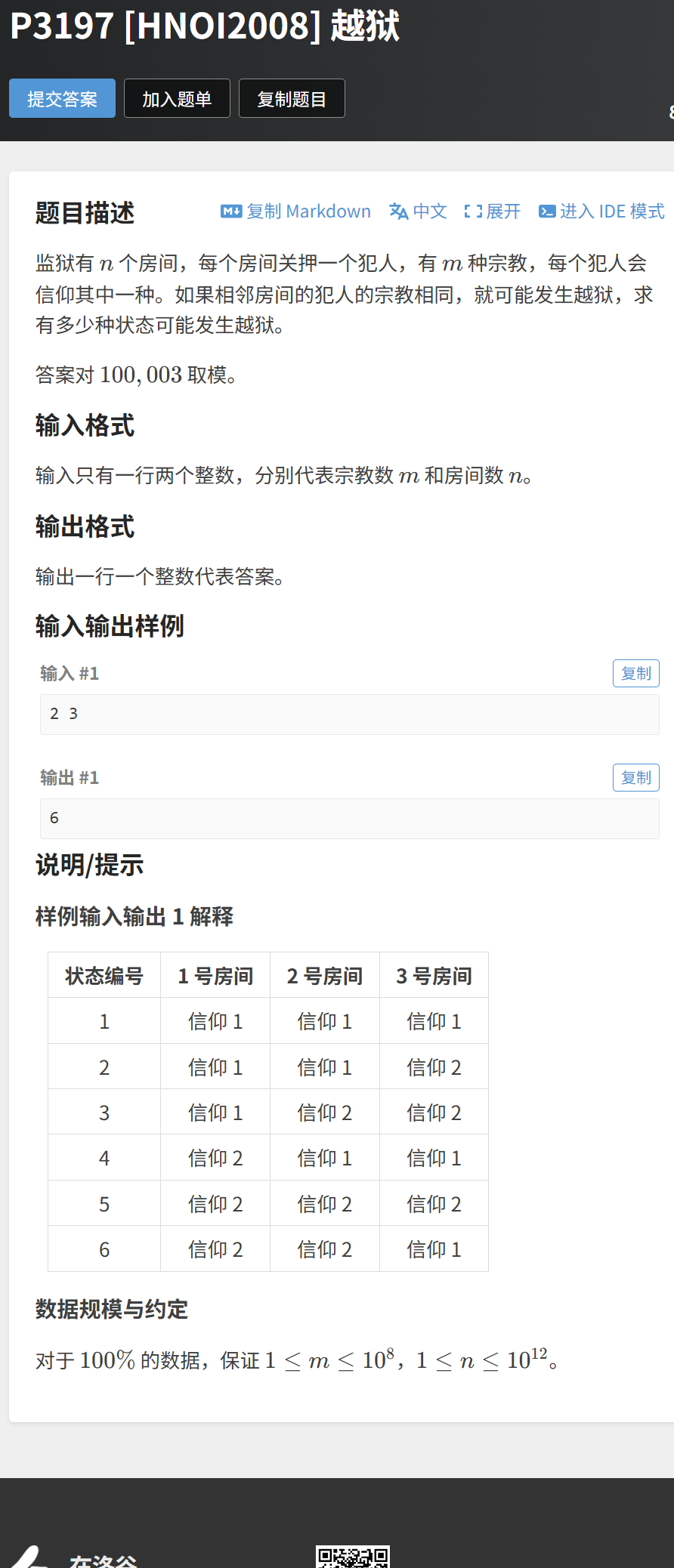
题目描述

监狱有 n 个房间，每个房间关押一个犯人，有 m 种宗教。若相邻房间的犯人信仰相同宗教，则可能发生越狱。求可能发生越狱的状态数（对 100003 取模）。

输入示例

2 3

输出示例

6

题目分析

这道题直接计算 “发生越狱” 的情况数较复杂（需要考虑至少一对相邻犯人宗教相同），但用 “正难则反” 的思路会很简单。

关键思路：总状态数 - 不发生越狱的状态数 = 发生越狱的状态数。

• 总状态数：每个犯人有 m 种宗教选择，共mn种。
• 不发生越狱的状态数：相邻犯人宗教不同。第一个犯人有 m 种选择，后面每个犯人都不能和前一个相同，有 m-1 种选择，共m×(m−1)n−1种。
• 越狱状态数 =

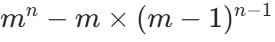
，结果对 100003 取模。

逻辑推导

以示例输入为例（m=2，n=3）：

• 总状态数：23=8。
• 不越狱状态数：2×(2-1)^(3-1) = 2×1=2（如 1-2-1、2-1-2）。
• 越狱状态数：8-2=6，和示例输出一致。

C++ 代码实现

#include <iostream>
using namespace std;

typedef long long LL;
const int MOD = 100003;

// 快速幂：计算a^b mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    a %= p; // 先取模，避免溢出
    while (b) {
        if (b & 1) ret = ret * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

int main() {
    LL m, n;
    cin >> m >> n;
    // 总状态数：m^n mod MOD
    LL total = qpow(m, n, MOD);
    // 不越狱状态数：m * (m-1)^(n-1) mod MOD
    LL no_escape = m * qpow(m - 1, n - 1, MOD) % MOD;
    // 越狱状态数 = (total - no_escape) mod MOD，避免负数
    LL escape = (total - no_escape + MOD) % MOD;
    cout << escape << endl;
    return 0;
}

代码注释

• 正难则反：避开复杂的 “至少一个相邻相同” 的计算，转化为简单的 “总状态数减无相邻相同”。
• 快速幂：高效计算大指数幂，避免溢出（a 先取模）。
• 防负数：由于 total 可能小于 no_escape，加 MOD 后再取模，确保结果为正。

难度总结

★★ 基础进阶，核心考察 “正难则反” 的计数技巧，这是组合计数中解决复杂约束问题的常用方法，必须掌握。

题目 6：车的放置（洛谷 P1350）—— 组合数 + 排列数，不规则图形的拆分

题目链接：https://www.luogu.com.cn/problem/P1350

题目描述

有一个不规则的网格棋盘，由 a、b、c、d 四个参数定义（具体形状见原题）。要在棋盘上放 k 个相互不攻击的车（即任意两车不在同一行、同一列），求方案数（对105+3取模）。

输入示例

2 2 2 2 2

输出示例

38

题目分析

车的放置问题是组合计数的经典模型，但这道题的棋盘是不规则的，需要先将其拆分为规则图形。

关键思路：拆分棋盘 + 分步计数。

• 不规则棋盘的拆分：将棋盘拆分为上下两个矩形（规则图形）：
  • 上矩形：行数为 a，列数为 b+d（左侧 b 列 + 右侧 d 列）。
  • 下矩形：行数为 c，列数为 d（右侧 d 列）。
• 车的放置约束：k 个车分为 x 个放在上矩形，k-x 个放在下矩形（x 从 0 到 k 枚举），满足：
  1. 上矩形的 x 个车：行不重复（选 x 行）、列不重复（选 x 列），且列不能和下矩形的车重复。
  2. 下矩形的 k-x 个车：行不重复（选 k-x 行）、列不重复（选 k-x 列），且列来自 d 列（和上矩形的右侧 d 列重叠）。
• 分步计算 x 对应的方案数：
  1. 上矩形选 x 个车：
     • 选 x 行：

     

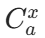
     （从 a 行选 x 行）。

     • 选 x 列：从 b+d 列中选 x 列，但这些列不能和下矩形的车重复。由于下矩形的车从 d 列中选，所以上矩形的车可选择的列分为两部分：左侧 b 列（无重叠）和右侧 d 列中未被下矩形选中的列。但更简单的方式是：先从 d 列中选 x 列给上矩形，再从 c 行中选 x 行给下矩形的车的列约束，最终推导得方案数为

     

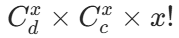
     （x!是列的排列数，因为车是不同的？不，车是相同的，但列的选择是有序的，因为每行对应不同的列）。

  2. 下矩形选 k-x 个车：
     • 选 k-x 行：

     

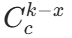
     （从 c 行选 k-x 行）。

     • 选 k-x 列：从 b+d -x 列（上矩形选了 x 列后剩下的）中选 k-x 列，方案数为

     

     。

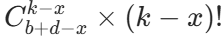
  3. x 对应的总方案数：上矩形方案数 × 下矩形方案数。
• 总方案数：枚举 x 从 0 到 k，累加所有 x 对应的方案数。

核心公式（x 对应的方案数）

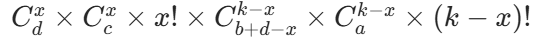
C++ 代码实现

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 2e3 + 10;
const int MOD = 1e5 + 3;

LL f[N]; // 阶乘数组：f[i] = i! mod MOD
LL g[N]; // 阶乘逆元数组：g[i] = (i!)^{-1} mod MOD

// 快速幂：计算a^b mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    while (b) {
        if (b & 1) ret = ret * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

// 初始化阶乘和逆元数组
void init() {
    int max_n = 2000; // 题目中a,b,c,d≤2000，k≤2000
    f[0] = 1;
    for (int i = 1; i <= max_n; ++i) {
        f[i] = i * f[i - 1] % MOD;
    }
    g[max_n] = qpow(f[max_n], MOD - 2, MOD);
    for (int i = max_n - 1; i >= 0; --i) {
        g[i] = (i + 1) * g[i + 1] % MOD;
    }
}

// 计算组合数C(n, m) mod MOD
LL C(int n, int m) {
    if (n < m) return 0;
    return f[n] * g[m] % MOD * g[n - m] % MOD;
}

int main() {
    init();
    LL a, b, c, d, k;
    cin >> a >> b >> c >> d >> k;
    
    LL result = 0;
    // 枚举x：上矩形放x个车，下矩形放k-x个车
    for (int x = 0; x <= k; ++x) {
        // 上矩形方案数：C(d, x) * C(c, x) * x!
        LL part1 = C(d, x) * C(c, x) % MOD;
        part1 = part1 * f[x] % MOD;
        
        // 下矩形方案数：C(b + d - x, k - x) * C(a, k - x) * (k - x)!
        LL part2 = C(b + d - x, k - x) * C(a, k - x) % MOD;
        part2 = part2 * f[k - x] % MOD;
        
        // 累加x对应的方案数
        result = (result + part1 * part2) % MOD;
    }
    cout << result << endl;
    return 0;
}

代码注释

• 棋盘拆分：将不规则棋盘拆分为上下两个矩形，简化计数。
• 组合数 + 排列数：车的放置需要 “选行 + 选列 + 排列”，排列数由阶乘表示（x! 表示 x 个列的全排列）。
• 枚举 x：遍历所有可能的拆分方式（x 从 0 到 k），累加方案数。

难度总结

★★ 进阶级，核心考察 “不规则图形拆分” 和 “组合数与排列数的结合”，需要具备将复杂问题分解为多个简单子问题的能力。

题目 7：数三角形（洛谷 P3166）—— 正难则反 + 数论（gcd），高阶应用

题目链接：https://www.luogu.com.cn/problem/P3166

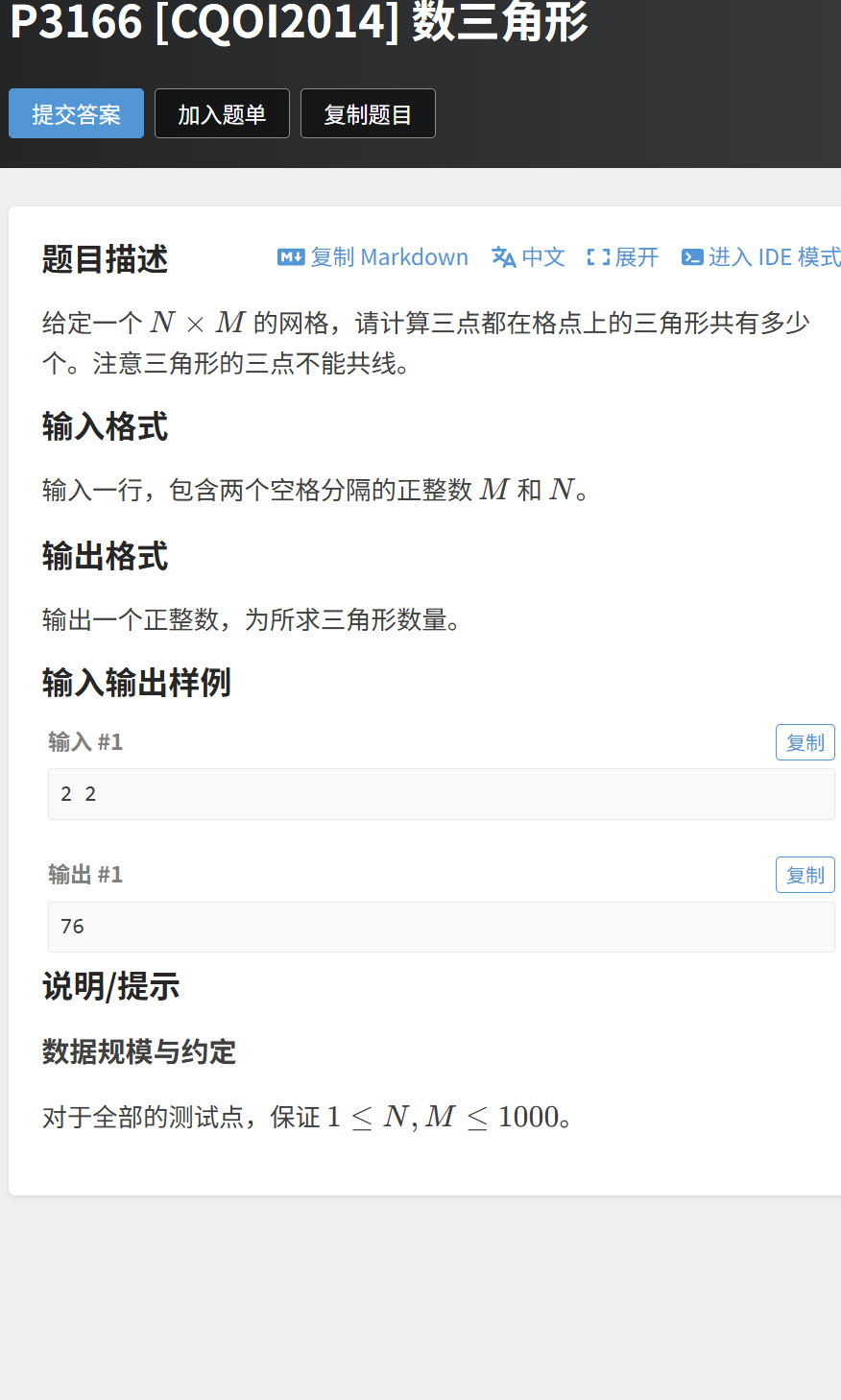
题目描述

给定一个 N×M 的网格，计算三点都在格点上的三角形个数（三点不能共线）。

输入示例

2 2

输出示例

76

题目分析

这道题是组合计数的高阶题目，直接计算 “不共线的三点” 较难，采用 “正难则反” 的思路：总三点数 - 共线的三点数 = 三角形个数。

关键思路：总三点数 - 共线三点数 = 答案。

1. 总三点数：网格的格点数为(N+1)×(M+1)（因为 N 行 M 列的网格有 N+1 条横线，M+1 条竖线，交点为格点）。从这些点中选 3 个，方案数为

​。

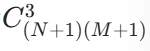
1. 共线三点数：分为三类 —— 水平共线、垂直共线、斜向共线（斜率为正或负）。
   • 水平共线：每行有(M+1)个点，选 3 个的方案数为

   

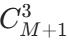
   ​，共(N+1)行，总方案数为

   

   。

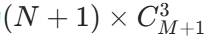
   • 垂直共线：每列有(N+1)个点，选 3 个的方案数为

   

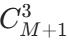
   ​，共(M+1)列，总方案数为

   

   ​。

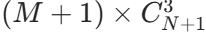
   • 斜向共线：这是最难的部分，需要用到数论中的 gcd（最大公约数）。
     • 斜率为正：考虑两个点(x1,y1)和(x2,y2)（x2>x1，y2>y1），两点之间的格点数（不含端点）为gcd(x2−x1,y2−y1)−1。
     • 若两点之间有 k 个格点，则这两点和其中任意一个格点可组成共线三点，方案数为 k。
     • 枚举所有可能的水平间隔 i（1≤i≤N）和垂直间隔 j（1≤j≤M），则这样的点对有(N−i+1)×(M−j+1)个（水平方向有 N-i+1 个起点，垂直方向有 M-j+1 个起点）。
     • 每个这样的点对对应的共线三点数为gcd(i,j)−1。
     • 斜率为负的情况和斜率为正的情况对称，所以总斜向共线三点数为

     

     。

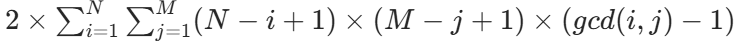
核心公式

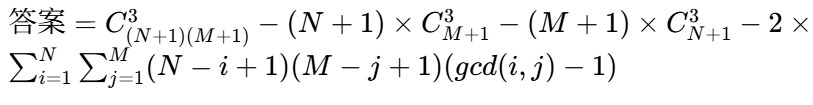
逻辑推导

以示例输入为例（N=2，M=2）：

• 格点数：(2+1)×(2+1)=9。
• 总三点数：C93​=84。
• 水平共线：(2+1)×C33​ = 3×1=3。
• 垂直共线：(2+1)×C33​ = 3×1=3。
• 斜向共线：
  • 枚举 i=1,j=1：gcd (1,1)-1=0，点对数量 (2-1+1)(2-1+1)=2×2=4，贡献 4×0=0。
  • i=1,j=2：gcd (1,2)-1=1-1=0，点对数量 (2-1+1)(2-2+1)=2×1=2，贡献 2×0=0。
  • i=2,j=1：gcd (2,1)-1=0，点对数量 (2-2+1)(2-1+1)=1×2=2，贡献 2×0=0。
  • i=2,j=2：gcd (2,2)-1=2-1=1，点对数量 (2-2+1)(2-2+1)=1×1=1，贡献 1×1=1。
  • 斜率为正的总贡献：0+0+0+1=1。
  • 斜率为负的贡献：1，总斜向共线：2×1=2。
• 共线三点数：3+3+2=8。
• 答案：84-8=76，和示例输出一致。

C++ 代码实现

#include <iostream>
using namespace std;

typedef long long LL;

// 计算最大公约数
LL gcd(LL a, LL b) {
    return b == 0 ? a : gcd(b, a % b);
}

int main() {
    LL n, m;
    cin >> n >> m;
    // 格点数：(n+1)*(m+1)
    LL total_points = (n + 1) * (m + 1);
    // 总三点数：C(total_points, 3)
    LL total = total_points * (total_points - 1) * (total_points - 2) / 6;
    
    // 水平共线三点数：(n+1)*C(m+1, 3)
    LL horizontal = (n + 1) * (m + 1) * m * (m - 1) / 6;
    // 垂直共线三点数：(m+1)*C(n+1, 3)
    LL vertical = (m + 1) * (n + 1) * n * (n - 1) / 6;
    
    // 斜向共线三点数
    LL diagonal = 0;
    for (LL i = 1; i <= n; ++i) { // 水平间隔i
        for (LL j = 1; j <= m; ++j) { // 垂直间隔j
            // 点对数量：(n - i + 1) * (m - j + 1)
            LL cnt = (n - i + 1) * (m - j + 1);
            // 共线三点数：(gcd(i,j) - 1) * cnt
            diagonal += cnt * (gcd(i, j) - 1);
        }
    }
    diagonal *= 2; // 斜率正负对称
    
    // 答案 = 总三点数 - 共线三点数
    LL ans = total - horizontal - vertical - diagonal;
    cout << ans << endl;
    return 0;
}

代码注释

• 正难则反：总三点数减去共线三点数，简化计算。
• 斜向共线计算：利用 gcd 求两点之间的格点数，枚举所有可能的间隔，累加贡献。
• 数论结合：gcd 是解决斜向共线问题的关键，需要理解 “两点间格点数 = gcd (水平间隔，垂直间隔)-1” 的原理。

难度总结

★★★ 高阶级，核心考察 “正难则反”“数论与组合计数的结合”，是算法竞赛中的经典题型，需要扎实的基础和灵活的思维。

三、组合计数解题思维总结

通过以上 7 道题的实战，我们可以总结出组合计数的核心解题思维：

1. 问题转化：将实际问题抽象为组合模型（如排序、分步计数、组合数、排列数）。
2. 正难则反：直接计数困难时，计算总方案数减去不符合条件的方案数（如越狱、数三角形）。
3. 拆分与合并：将复杂问题拆分为多个简单子问题，分别计数后合并（如车的放置、编号问题）。
4. 数论辅助：高阶问题常需要结合 gcd、幂运算、逆元等数论知识（如数三角形、组合数取模）。
5. 公式记忆：熟练掌握组合数、阶乘、逆元的计算的公式和代码实现。

总结

组合计数不是孤立的公式记忆，而是一系列思维方法的综合应用。本文的 7 道题覆盖了从入门到高阶的核心考点，每道题都对应一种关键思维技巧。 学习组合计数的关键的是：多做题、多总结，遇到新题时先尝试拆解问题，思考 “这道题可以转化为哪种组合模型？”“是否可以用正难则反？”“是否需要拆分问题？”。 希望本文能帮助你打通组合计数的 “任督二脉”，在后续的算法竞赛和实际应用中灵活运用！如果有任何疑问或建议，欢迎在评论区留言交流～