LLaMA架构参数量和计算量估算

经典Transformer为基础的大模型，其架构总体上可以分为三类，自回归（Auto- regressive），自编码（Auto-encoding），编码解码（Encoder-Decoder）。其中以GPT和LLaMA为代表自回归架构，无论在模型数量还是下游任务表现中一骑绝尘。本节围绕自回归架构介绍：

1）自回归架构中多头注意力和前馈网络模块的参数估计。 2）输入token数量、模型参数量与总计算量之间的关系。 3）给定训练数据、模型量级和GPU算力情况下，全参数训练一轮需要的时间。

1，大模型参数量估计

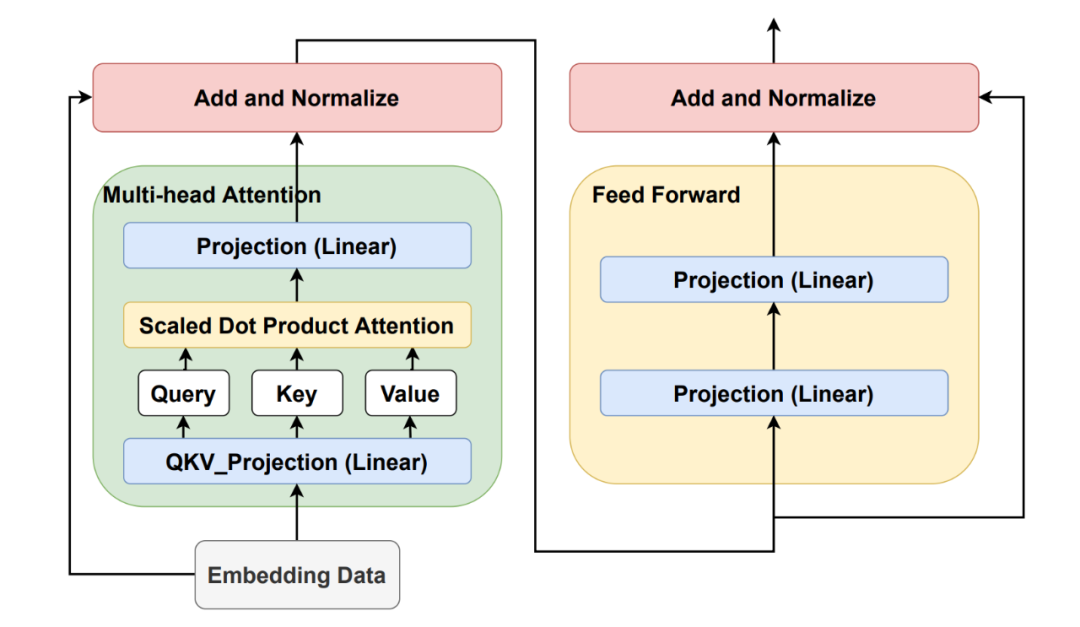
图1，LLaMA架构，其中一层包含多头注意力MHA和前馈网络FFN模块。

• • 符号定义

输入向量为 , 其中 b为batch_size，s 为序列长度，h为隐层向量维度。下面以一层的block进行参数量的估算，总的参数量乘以总共的层数 L 即可。

• • 多头注意力层 MHA

在注意力输出时，有一个输出参数矩阵 ，使得输入和输出维度保持一致。四个可训练参数 。所以注意力层可训练的参数量为

• • 前馈层 FFN

一般前馈网络先升级输出向量的维度，然后再降低到原维度。基于此的可训练的参数量为

• • 残差连接和归一化

为了使每一层的输入和输出稳定在一个合理的范围内，使用了层归一化。一共有2个归一化层，每一层有2个参数，总参数量为 。

以上参数量加和并且乘以 l 层的block，即：

小结：当h比较大时，忽略掉一次项，得到参数量为 。 以不同版本的LLaMA模型进行参数估计验证。

2，大模型计算量估计

2.1, 多头注意力 MHA

• 线性层部分

，，

得到三个变量需要的计算量为 。

公式可分为两部分，第一部分，bsh为总的元素个数；第二部分，根据矩阵运算，每一个元素是由h次的乘法和h-1次的加法计算而来。

• • 计算

假设多头数为a，则注意力分数矩阵score的维度信息为：[b,a,s,s]

得到的向量维度为 相应的计算量为：。注意

• • 注意力分数矩阵score和矩阵 V 的计算量
• • 输出的线性层

小结：总的计算量为：

2.2，前馈网络FFN

• • 升维：
• • 降维：

小结：FFN 总共的计算量为：。

加和MHA和FFN就是单个block层的计算量，再乘以总共的层数l，即为前向计算一次总共的计算量，如下公式：

此时有多种情形需要区分：

1）当输入的序列长度 s 比较小时，h的平方占主要的计算量。比如使用65B的LLaMA模型此时 h=8192，如果输入的长度s=1K左右，那主要的计算量来自于h的二次项。此时可以省略一次项。

2）如果当输入的长度 s 和隐藏层 h 相当时，即输入序列的平均长度 s=10K左右，此时要考虑输入s的影响，可以将两项近似相加表示成

3）如果输入序列的平均长度s，大于或远大于隐藏层 h 时，比如s=102K，此时输入长度s的二次方占主要的计算量，模型的计算量主要来源于多头注意力MHA部分。

下面以第一种情况为背景估计训练时间，即输入序列的长度较小，此时h的二次方占主要计算量。

2.3，训练时间估计

• • 计算量，参数量和数据量关系

通过公式，可以粗略的得到计算量，参数量和数据量之间的关系。bs 可认为是一次性输入模型的token数量。

忽略一次项，可知每个参数和token 在前向过程中都需要进行两个浮点运算，可以理解为一次乘法和一次加法。

• • 训练耗时估算

前提：对于计算量，初步证明反向计算是前向计算的2倍。为减少了中间激活值的显存占用，需要重新计算激活值，其计算量和前向计算量相同。

计算耗时等于总的算力需求，除以单位时间内总共的GPU算力。计算公式如下：

参数量个数峰值算力利用率

其中系数 8 是， 前向计算 2 + 反向传播 4 + 激活重计算 2 = 8。以GPT3-175B 模型为例，总的数据量为 300B，在1024张 40G显存的A100 上进行训练，已知A100 FP16 的算力为 312 TFLOPS，假设显卡的利用率为 0.45，需要的训练时间为：

总结

• • 自回归代表架构GPT和LLaMA模型，其参数量可通过block层数和隐藏层维度，通过公式 快速估算大模型的参数。
• • 完成一次前向计算，模型参数和输入token，都需要进行两次运算，一次乘法一次加法。
• • 计算量估算，不仅涉及block层数和隐藏层维度，还与输入的token量相关，可通过公式 估算。

以此为基础，了解了大模型的参数后，并在已有算力和token语料的情况下，训练一个大模型需要的时间也可轻松计算出。

参考： [1] arxiv: 2110.14883