完成对六位半电压表的极限参数建模(YUNSWJ仓促版)
之前写了比较多的多位表的内容,但是相关的建模内容很少,今天就写一些。

K2000
K2000
什么叫“位”和“半位”(核心定义)
“位(digit)”不是小数位,而是“显示计数位”
在万用表里:
1 位 = 1 个完整的十进制数字(0–9)
能完整显示 0~9,称为 1 位
能显示 0 或 1(有时到 2),称为 半位(½ digit)
六位半 = 6 个完整数字 + 1 个“最高位受限数字”
6½ 位显示能力 = 1999999 counts(≈ 2,000,000 counts)
类型 | 最大显示 | 对应 counts |
|---|---|---|
5½ 位 | 199999 | 200k |
6½ 位 | 1999999 | 2M |
7½ 位 | 19999999 | 20M |
重点:
“位数”描述的是 ADC 输出+显示系统的动态范围,不是精度本身。
6½ 位到底“能分辨多细”?(分辨率)
我们以最典型的 10 V 档 为例:
分辨率公式
量程
六位半在 10 V 档
也就是说:
显示:10.000000 V
最小显示变化 = 5 µV
实际常标称为 1 µV 级分辨率
注意:
这是“分辨率”,不是“误差”
分辨率 ≠ 精度 ≠ 准确度
很多人第一次都会混淆这三件事。
三个概念对比
名称 | 看到的 | 决定因素 |
|---|---|---|
分辨率 | 最小跳变 | 位数 / counts |
精度(Accuracy) | 离真值多远 | 校准、漂移、线性 |
重复性 | 抖不抖 | 噪声、积分时间 |
一个典型 6½ 位表的现实指标
以 Keithley 2000 为例:
分辨率:1 µV
一年 DCV 精度:≈ 30–50 ppm
噪声(NPLC=1):~3–5 µV RMS
噪声(NPLC=10):~0.7–1 µV RMS
所以:
能“显示”1 µV,不代表“测得准”1 µV
6½ 位是怎么“测出来”的?(ADC 架构)
几乎所有台式 6½ 位表都用:
积分型 ADC(双积分,多斜率积分(MSI))
核心思想
用时间换精度,用积分抑制噪声
把输入电压 → 转换成 积分时间,里面的参考源、电容、运放参数误差会被抵消,这样就对 50 / 60 Hz 干扰天然免疫
这也是为什么会看到一个参数叫:
NPLC(Number of Power Line Cycles)
NPLC | 积分时间 | 特性 |
|---|---|---|
0.1 | 2 ms | 快,噪声大 |
1 | 20 ms | 标准 |
10 | 200 ms | 低噪声 |
100 | 2 s | 极限稳定 |
结论:
6½ 位不是“瞬时精度”,而是“积分后的精度”
6½ 位 vs ADC ENOB
很多做 ADC 的人会问:
“6½ 位 ≈ 几位 ADC?”
粗略等效:
但注意:这是 直流 + 积分后的等效和高速 ADC 的 ENOB 不可直接类比,因为它追求的是 低频、直流、长期稳定。
用数学模型推导 6½ 位积分 ADC 的噪声极限
用数学模型把“6½ 位积分 ADC(以双积分/多斜率积分为代表)能做到的噪声极限”推出来。前置假设是:
- 把积分型 ADC 看成一个线性滤波器 + 采样/比值测量器
- 用滤波器的 ENBW(等效噪声带宽)把各种噪声源折算到输出
- 把输出噪声换算成 counts,看它能不能支撑 6½ 位(2,000,000 counts)
建模对象与符号
以最典型的 双积分(dual-slope)为主(多斜率只是把“回零阶段”做得更精密,噪声推法类似):
输入电压:
参考电压:(回零阶段用)
积分时间(run-up):
回零时间(run-down):
积分器输出:
积分器输入等效噪声:(包含前端热噪声/放大器/开关注入折算等)
理想双积分的测量式(忽略误差项):
所以:输出读数本质上是“时间比值”。噪声会让这个比值抖动。
关键一步:双积分对输入噪声的“滤波器等效”
把积分过程写成线性算子。积分器(电容 ,电阻 ):
在 run-up 结束时():
run-down 阶段用 反向积分直到 。设实际回零时间为 。写“回零条件”:
整理得到:
噪声积分项
因此估计的输入电压:
这给了一个非常重要的结论:
双积分对“输入等效电压噪声”就是做了两段矩形窗的积分,再除以 ,所以它等效成一个“平均器(averager)”。
为了得到噪声 RMS,我们把上式看成线性滤波器输出:
其中权函数(简单近似 时最常用):
也就是“长度 的矩形平均”,幅度 。
白噪声下的噪声极限
设输入等效噪声是白噪声,单边谱密度(单位 V/√Hz)为 (常数)。
定理: 对白噪声,通过线性滤波器,输出方差
其中 ENBW 是滤波器等效噪声带宽。
矩形平均器的 ENBW
长度 的“平均器”权函数
其 ENBW 为:
这个结果非常经典:平均越久,带宽越窄,噪声越低。
这里双积分近似等效平均长度 ,于是:
所以输出 RMS 噪声极限(白噪声):
这就是我们要的“噪声极限公式”之一:
积分时间 翻 4 倍,噪声 RMS 降一半()
把 NPLC 放进来:和电网频率的直接关系
台式 DMM 常设:
例如 50 Hz 下:1 NPLC = 20 ms;60 Hz 下:1 NPLC ≈ 16.67 ms。
代入上式:
这条特别好用:
NPLC 越大,噪声按 降,也解释了为什么“慢档更稳、噪声更低”
6½ 位的“counts 噪声”门槛怎么判?
6½ 位约等于 2,000,000 counts。对某个量程 (比如 10 V 档),1 count 约为:
要让显示“稳定到最后几位”,经验上希望: LSB(取决于显示/滤波策略)
换成对噪声密度的要求:
如果以“1 LSB”为目标:
这给了一个非常清晰的工程含义:
想撑住 6½ 位,输入等效噪声密度 必须低到:与量程成正比、与积分时间的平方根成正比。
1/f 噪声怎么进来?
上面白噪声很好推,但真实 DMM 在长积分时,常被 1/f 噪声、漂移、温漂、热电势限制。
典型 1/f 噪声模型:
单位
输出方差:
对“平均器” 低频处 ,因此 1/f 噪声积分会出现对低频截止的依赖:
大致由滤波器主瓣决定(~1/T)
由“观测时间/零点漂移补偿/auto-zero”等决定(不是数学上自然出现的,必须由系统机制给出)
白噪声随着 增长一直降,但 1/f 和漂移会让我们在大 NPLC 时出现“继续变慢,改善不明显甚至变差”的拐点,这就是很多表在 NPLC=10、100 时提升有限的原因之一。
参考源噪声的极限(双积分的第二大噪声项)
因为结果是比值 ,参考噪声会直接乘进去;把参考噪声看成 。在 run-down 阶段,回零时间由“积分到零”决定,参考噪声会等效成时间抖动,再折算成电压噪声。
工程上常用一个近似:参考噪声在 run-down 的“有效平均”后,以比例形式进入:
其中 是参考在 上平均后的 RMS:
所以在大信号测量时,参考噪声会决定“有效位数”的上限;在小信号时,前端噪声/热电势更关键。
一个可直接用的“噪声预算”总公式
把主要噪声项近似平方和(RMS):
输入白噪声参考噪声折算漂移近似热电势接触噪声等
然后换算到 counts:
判据(经验性的看):
:最后一位较稳,更小会“钉死”,但也可能掩盖真实漂移(看用途)
噪声极限
在“白噪声主导、双积分、”的理想极限下:
这就是“积分 ADC 的噪声极限标尺”。
继续推导: 6½ 位的门槛线
先用一组“典型台式 DMM 前端噪声密度”的假设值,做一张从 0.1 到 100 NPLC 的极限曲线,把 6½ 位的门槛线标出来。
再用一组“典型台式 DMM 前端输入等效白噪声密度”的假设值,画出了 0.1–100 NPLC 的双积分(dual-slope)白噪声极限曲线,并把 6½ 位门槛线标出来了(以 10 V 量程、2,000,000 counts 为例:1 LSB = 5 µV)。
在下面看到两张图:
σV(伏特 RMS) vs NPLC:并标出 1 LSB = 5 µV、0.3 LSB ≈ 1.5 µV 两条水平线
σ(counts RMS) vs NPLC:更直观地看“最后一位稳不稳”(1 count、0.3 count 门槛)
用的数学模型
对双积分在“白噪声主导、”近似下:
并用 50 Hz 作为电网频率(60 Hz 时整体会略变差一点点,因为 )。
6½ 位在 10 V 档:

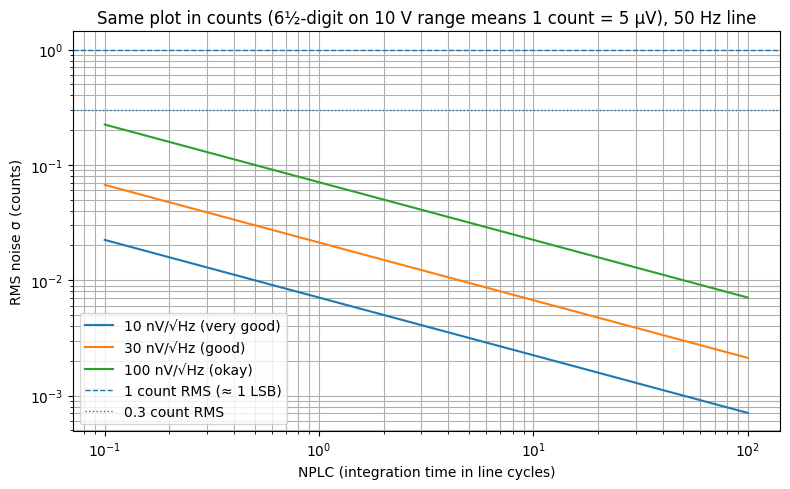
image-20260102130747411
Assumptions: 50 Hz line, 10 V range, 6½-digit => 1 LSB = 5.00 µV
NPLC points: [ 0.1 1. 10. 100. ]
10 nV/√Hz (very good)
NPLC= 0.1: σ_V= 0.112 µV, σ= 0.022 counts
NPLC= 1.0: σ_V= 0.035 µV, σ= 0.007 counts
NPLC= 10.0: σ_V= 0.011 µV, σ= 0.002 counts
NPLC=100.0: σ_V= 0.004 µV, σ= 0.001 counts
30 nV/√Hz (good)
NPLC= 0.1: σ_V= 0.335 µV, σ= 0.067 counts
NPLC= 1.0: σ_V= 0.106 µV, σ= 0.021 counts
NPLC= 10.0: σ_V= 0.034 µV, σ= 0.007 counts
NPLC=100.0: σ_V= 0.011 µV, σ= 0.002 counts
100 nV/√Hz (okay)
NPLC= 0.1: σ_V= 1.118 µV, σ= 0.224 counts
NPLC= 1.0: σ_V= 0.354 µV, σ= 0.071 counts
NPLC= 10.0: σ_V= 0.112 µV, σ= 0.022 counts
NPLC=100.0: σ_V= 0.035 µV, σ= 0.007 counts
仅从“白噪声极限”看:6½ 位门槛其实很宽松
会发现,即便假设输入等效白噪声密度到 100 nV/√Hz(我标成“okay”),在 50 Hz 下:
NPLC=0.1:σ ≈ 0.224 counts RMS
NPLC=1:σ ≈ 0.071 counts RMS
NPLC=10:σ ≈ 0.022 counts RMS
也就是说:白噪声并不会卡在 6½ 位,它远低于 1 count 的门槛。
这对应一个现实经验:
真实 6½ 位表的“最后几位跳动”,更多来自 1/f 噪声、漂移、热电势、开关注入、参考源低频噪声、温漂与机械/接触噪声,而不是白噪声。
6½ 位“能不能冻结最后一位”的主导不是 NPLC,而是低频误差机制
所以真实机器上常见到:
NPLC 从 1 拉到 10:明显更稳
从 10 拉到 100:改善变小,甚至出现慢漂、慢跳(因为 1/f 与热漂移开始主导)
继续完善
加入:
1/f 噪声项:(决定大 NPLC 的拐点)
热电势/漂移项:可用随机游走或线性漂移 + 温度噪声模型叠加
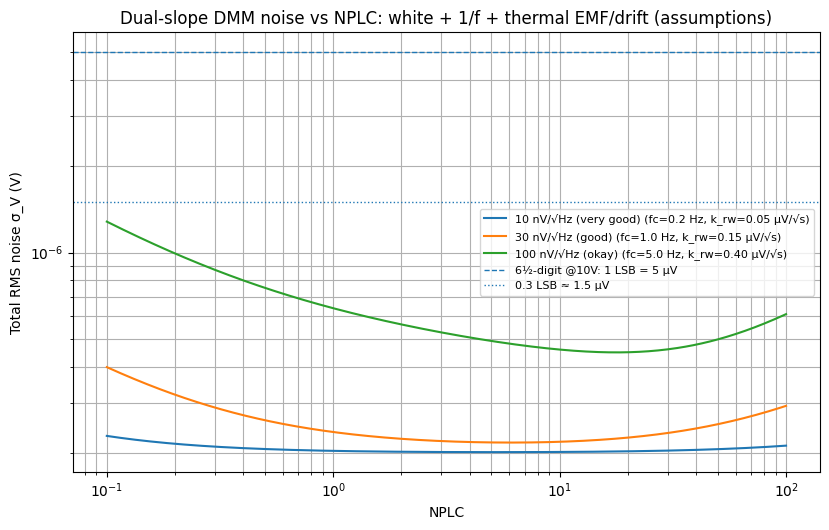
image-20260102131101936
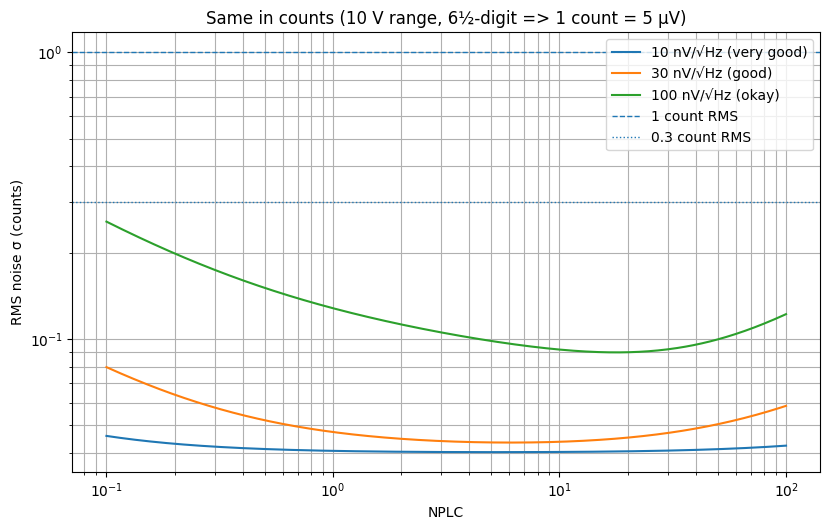
image-20260102131107344
Assumed parameters:
Line freq: 50.0 Hz, Ti = NPLC/f_line
10 V range, 6½-digit => 1 LSB = 5.00 µV
1/f low cutoff via auto-zero timescale T_az = 5.0 s (f_L=0.200 Hz)
Component breakdown for '30 nV/√Hz (good)': en=30.0 nV/√Hz, f_c=1.0 Hz, k_rw=0.15 µV/√s
NPLC= 0.1: white= 0.335 µV, 1/f= 0.080 µV, drift= 0.200 µV => total= 0.399 µV (0.080 counts)
NPLC= 1.0: white= 0.106 µV, 1/f= 0.066 µV, drift= 0.201 µV => total= 0.237 µV (0.047 counts)
NPLC= 10.0: white= 0.034 µV, 1/f= 0.048 µV, drift= 0.211 µV => total= 0.219 µV (0.044 counts)
NPLC=100.0: white= 0.011 µV, 1/f= 0.014 µV, drift= 0.292 µV => total= 0.292 µV (0.058 counts)
把 1/f 噪声 和 热电势/漂移(低频游走) 两个机制都加到模型里,并重新画了两张“极限曲线”:
总 RMS 噪声 σV vs NPLC(0.1–100),并标出 6½ 位门槛线(10 V 档:1 LSB = 5 µV、0.3 LSB = 1.5 µV)
同一张图换算成 counts(更直观判断最后一位抖不抖)
会明显看到:曲线不再是一直往下掉,而是出现了“U 型 / 拐点”——这正是现实 DMM 的典型现象: 短积分时白噪声主导,积分变长后 1/f 与漂移开始主导,继续变慢收益变小甚至变差。
加的两个项:数学形式
白噪声项(之前那条)
1/f 噪声项(用“1/f 角频率”表征)
设 1/f 噪声 PSD:。 对“平均器/双积分等效低通”,取:
上限
下限 (用一个“autozero/反转/归零的有效时间尺度”来截断发散)
得到:
我假设:。
热电势/漂移项(低频游走的简化随机游走模型)
用随机游走系数 表征“热电势/接触/温漂导致的慢漂”:
其中 是一个小的“微热扰动底噪”(我设 0.2 µV)。
总噪声
结果怎么解读?
以我给的“good 级别”假设(30 nV/√Hz,,)为例(50 Hz,10 V 档):
NPLC=0.1:总噪声 ≈ 0.399 µV(0.080 counts)
NPLC=1:总噪声 ≈ 0.237 µV(0.047 counts)
NPLC=10:总噪声 ≈ 0.219 µV(0.044 counts)
NPLC=100:总噪声 ≈ 0.292 µV(0.058 counts)
能看到:从 1 到 10 提升不大;到 100 反而变差一点点(漂移项开始抬头)。
同时也能看到另一个事实:即便加入 1/f + 漂移,在 10 V 档“1 LSB=5 µV”的 6½ 位门槛仍然很宽松(远低于 1 count RMS)。
这也符合现实:6½ 位表在 10 V 档通常“最后几位”更多是显示滤波策略、短时抖动、以及环境热电势导致的慢漂,而不是白噪声限制。
后记
我虽然不做这么高级的表,但是我会算,仓促是因为回家一直在修东西,写一会儿就得出去修一会儿,时间被打碎.
import numpy as np
import matplotlib.pyplot as plt
# -----------------------------
# Model: Dual-slope DMM noise vs NPLC
# Add: white noise + 1/f noise + thermal EMF / drift (random walk)
# -----------------------------
f_line = 50.0 # Hz
nplc = np.logspace(-1, 2, 500) # 0.1..100
T = nplc / f_line # integration time (seconds), using Ti = NPLC / f_line
# Range and counts for "6½-digit @10V"
V_FS = 10.0
counts = 2_000_000
V_LSB = V_FS / counts # 5 µV
# --- White noise (input-referred) assumptions (V/sqrt(Hz)) ---
en_list = [
("10 nV/√Hz (very good)", 10e-9),
("30 nV/√Hz (good)", 30e-9),
("100 nV/√Hz (okay)", 100e-9),
]
# Dual-slope white-noise limit (approx): sigma_w = e_n /(2*sqrt(Ti))
def sigma_white(en, Ti):
return en / (2.0 * np.sqrt(Ti))
# --- 1/f noise model ---
# Define 1/f corner where 1/f equals white at f_c:
# sqrt(S_1f(f)) = en * sqrt(f_c/f) (V/sqrt(Hz))
# so PSD: S_1f(f) = en^2 * f_c / f (V^2/Hz)
#
# For an averaging-like transfer function, low-f |H(f)|~1 up to ~f_H ~ 1/(2Ti) (order),
# and the effective lower bound f_L set by auto-zero / reversal / calibration cadence.
# We'll model f_L as 1 / T_az, with a plausible T_az = 1..10 s for DMM-style zero/offset tracking.
T_az = 5.0 # seconds (assumed effective low-frequency "reset" / autozero timescale)
f_L = 1.0 / T_az
# Use f_H ~ 1/(2Ti) (captures that longer integration narrows passband)
def sigma_1f(en, f_c, Ti):
f_H = 1.0 / (2.0 * Ti)
# ensure f_H >= f_L to avoid negative log; if not, clamp -> log=0 meaning 1/f largely averaged out below f_L
ratio = np.maximum(f_H / f_L, 1.0)
var = (en**2 * f_c) * np.log(ratio)
return np.sqrt(var)
# Pick plausible 1/f corners for each "quality" level (order-of-magnitude)
# Better front-end has lower corner (less 1/f) and/or uses chopper/AZ.
f_c_map = {
"10 nV/√Hz (very good)": 0.2, # Hz
"30 nV/√Hz (good)": 1.0, # Hz
"100 nV/√Hz (okay)": 5.0, # Hz
}
# --- Thermal EMF / drift model ---
# Thermal EMF + contact noise often behaves like low-frequency wander.
# Simple model: random walk of offset with coefficient k_rw (V/sqrt(s)),
# and the "measurement" averages over Ti, so RMS contribution scales ~ k_rw * sqrt(T_obs) / sqrt(N_eff).
# A pragmatic way: treat it as sigma_drift = k_rw * sqrt(Ti) (grows with time)
# plus a small "floor" (e.g., due to micro-thermals that don't average).
k_rw_map = {
"10 nV/√Hz (very good)": 0.05e-6, # 0.05 µV/sqrt(s)
"30 nV/√Hz (good)": 0.15e-6, # 0.15 µV/sqrt(s)
"100 nV/√Hz (okay)": 0.40e-6, # 0.40 µV/sqrt(s)
}
sigma_floor = 0.2e-6 # 0.2 µV RMS "micro-thermal" floor
def sigma_drift(k_rw, Ti):
return np.sqrt((k_rw**2) * Ti + sigma_floor**2)
# --- Compute and plot ---
plt.figure(figsize=(8.4, 5.4))
for label, en in en_list:
f_c = f_c_map[label]
k_rw = k_rw_map[label]
s_w = sigma_white(en, T)
s_1f = sigma_1f(en, f_c, T)
s_d = sigma_drift(k_rw, T)
s_tot = np.sqrt(s_w**2 + s_1f**2 + s_d**2)
plt.loglog(nplc, s_tot, label=f"{label} (fc={f_c} Hz, k_rw={k_rw*1e6:.2f} µV/√s)")
# 6½-digit thresholds on 10V range
plt.axhline(V_LSB, linestyle="--", linewidth=1, label="6½-digit @10V: 1 LSB = 5 µV")
plt.axhline(0.3*V_LSB, linestyle=":", linewidth=1, label="0.3 LSB ≈ 1.5 µV")
plt.xlabel("NPLC")
plt.ylabel("Total RMS noise σ_V (V)")
plt.title("Dual-slope DMM noise vs NPLC: white + 1/f + thermal EMF/drift (assumptions)")
plt.grid(True, which="both")
plt.legend(fontsize=8)
plt.tight_layout()
plt.show()
# counts plot
plt.figure(figsize=(8.4, 5.4))
for label, en in en_list:
f_c = f_c_map[label]
k_rw = k_rw_map[label]
s_w = sigma_white(en, T)
s_1f = sigma_1f(en, f_c, T)
s_d = sigma_drift(k_rw, T)
s_tot = np.sqrt(s_w**2 + s_1f**2 + s_d**2)
plt.loglog(nplc, s_tot / V_LSB, label=f"{label}")
plt.axhline(1.0, linestyle="--", linewidth=1, label="1 count RMS")
plt.axhline(0.3, linestyle=":", linewidth=1, label="0.3 count RMS")
plt.xlabel("NPLC")
plt.ylabel("RMS noise σ (counts)")
plt.title("Same in counts (10 V range, 6½-digit => 1 count = 5 µV)")
plt.grid(True, which="both")
plt.legend()
plt.tight_layout()
plt.show()
# Show component breakdown for "good" case at representative NPLC
label_sel = "30 nV/√Hz (good)"
en_sel = dict(en_list)[label_sel]
f_c_sel = f_c_map[label_sel]
k_rw_sel = k_rw_map[label_sel]
points = np.array([0.1, 1, 10, 100.0])
Ti_p = points / f_line
s_w = sigma_white(en_sel, Ti_p)
s_1f = sigma_1f(en_sel, f_c_sel, Ti_p)
s_d = sigma_drift(k_rw_sel, Ti_p)
s_tot = np.sqrt(s_w**2 + s_1f**2 + s_d**2)
print("Assumed parameters:")
print(f" Line freq: {f_line} Hz, Ti = NPLC/f_line")
print(f" 10 V range, 6½-digit => 1 LSB = {V_LSB*1e6:.2f} µV")
print(f" 1/f low cutoff via auto-zero timescale T_az = {T_az} s (f_L={f_L:.3f} Hz)")
print(f"\nComponent breakdown for '{label_sel}': en={en_sel*1e9:.1f} nV/√Hz, f_c={f_c_sel} Hz, k_rw={k_rw_sel*1e6:.2f} µV/√s")
for n, w, onef, d, tot in zip(points, s_w, s_1f, s_d, s_tot):
print(f" NPLC={n:>5}: white={w*1e6:>6.3f} µV, 1/f={onef*1e6:>6.3f} µV, drift={d*1e6:>6.3f} µV => total={tot*1e6:>6.3f} µV ({tot/V_LSB:>5.3f} counts)")
import numpy as np
import matplotlib.pyplot as plt
# 支持中文 + 正确显示负号
# import matplotlib.pyplot as plt
# 设置支持更多符号的字体
plt.rcParams['font.sans-serif'] = ['DejaVu Sans', 'SimHei'] # fallback 到 SimHei 显示中文
plt.rcParams['axes.unicode_minus'] = False # 避免 U+2212 减号问题
# Assumptions (typical bench DMM front-end, order-of-magnitude)
f_line_50 = 50.0 # Hz
f_line_60 = 60.0 # Hz
# NPLC sweep
nplc = np.logspace(-1, 2, 400) # 0.1 ... 100
# Typical input-referred white-noise density assumptions (V/sqrt(Hz))
en_list = [
("10 nV/√Hz (very good)", 10e-9),
("30 nV/√Hz (good)", 30e-9),
("100 nV/√Hz (okay)", 100e-9),
]
# Dual-slope white-noise limit: sigma_V ≈ (e_n/2)*sqrt(f_line/NPLC)
def sigma_v(en, f_line, nplc):
return (en / 2.0) * np.sqrt(f_line / nplc)
# 6½-digit threshold on 10 V range: 2,000,000 counts -> 1 LSB = 10V/2e6 = 5 µV
V_FS = 10.0
counts = 2_000_000
V_LSB = V_FS / counts # volts
V_1LSB = V_LSB
V_0p3LSB = 0.3 * V_LSB
# --- Plot 1: sigma_V vs NPLC (50 Hz) with 6½-digit thresholds ---
plt.figure(figsize=(8, 5))
for label, en in en_list:
plt.loglog(nplc, sigma_v(en, f_line_50, nplc), label=label)
plt.axhline(V_1LSB, linestyle="--", linewidth=1, label="6½-digit @10V: 1 LSB = 5 µV")
plt.axhline(V_0p3LSB, linestyle=":", linewidth=1, label="0.3 LSB ≈ 1.5 µV")
plt.xlabel("NPLC (integration time in line cycles)")
plt.ylabel("RMS output noise floor σ_V (V)")
plt.title("Dual-slope white-noise limit vs NPLC (assumed input-referred white noise, 50 Hz line)")
plt.grid(True, which="both")
plt.legend()
plt.tight_layout()
plt.show()
# --- Plot 2: same but in counts (50 Hz) ---
plt.figure(figsize=(8, 5))
for label, en in en_list:
sig_counts = sigma_v(en, f_line_50, nplc) / V_LSB
plt.loglog(nplc, sig_counts, label=label)
plt.axhline(1.0, linestyle="--", linewidth=1, label="1 count RMS (≈ 1 LSB)")
plt.axhline(0.3, linestyle=":", linewidth=1, label="0.3 count RMS")
plt.xlabel("NPLC (integration time in line cycles)")
plt.ylabel("RMS noise σ (counts)")
plt.title("Same plot in counts (6½-digit on 10 V range means 1 count = 5 µV), 50 Hz line")
plt.grid(True, which="both")
plt.legend()
plt.tight_layout()
plt.show()
# Quick numeric table at a few NPLC points
test_nplc = np.array([0.1, 1, 10, 100.0])
rows = []
for label, en in en_list:
sig_uV = sigma_v(en, f_line_50, test_nplc) * 1e6
sig_counts = sigma_v(en, f_line_50, test_nplc) / V_LSB
rows.append((label, sig_uV, sig_counts))
print(f"Assumptions: 50 Hz line, 10 V range, 6½-digit => 1 LSB = {V_LSB*1e6:.2f} µV")
print("NPLC points:", test_nplc)
for label, sig_uV, sig_counts in rows:
print(f"\n{label}")
for n, u, c in zip(test_nplc, sig_uV, sig_counts):
print(f" NPLC={n:>5}: σ_V={u:>8.3f} µV, σ={c:>8.3f} counts")本文参与 腾讯云自媒体同步曝光计划,分享自微信公众号。
原始发表:2026-01-02,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录


