数据库圣经--从原理到实战，一文彻底搞懂 InnoDB 索引

一、索引的简介 1、什么是索引

        MySQL的索引是⼀种数据结构，它可以帮助数据库高效地查询、更新数据表中的数据。索引通过一定的规则排列数据表中的记录，使得对表的查询可以通过对索引的搜索来加快速度。

         MySQL索引类似于书籍的目录，通过指向数据行的位置，可以快速定位和访问表中的数据，比如汉语字典的目录（索引）页，我们可以按笔画、偏旁部首、拼音等排序的目录（索引）快速查找到需要的字。

2、为什么要使用索引

        显而易见，使用索引的目的只有⼀个，就是提升数据检索的效率，在应用程序的运行过程中，查询操作的频率远远高于增删改的频率。

二、索引应该选择哪种数据结构

1、HASH

        时间复杂度是 O(1) ，查询速度非常快，但是MySQL并没有选择HASH做为索引的默认数据结 构，主要原因是HASH不支持范围查找

2、二叉搜索树

        ⼆叉搜索树的中序遍历是⼀个有序数组，但有几个问题导致它不适合用作索引的数据结构

（1）最坏情况下时间复杂度为O(N)

（2）节点个数过多无法保证树高

        AVL和红黑树，虽然是平衡或者近似平衡，但是毕竟是⼆叉结构

        在检索数据时，每次访问某个节点的子节点时都会发生⼀次磁盘IO，而在整个数据库系统中，IO是性能的瓶颈，减少IO次数可以有效的提升性能

1. 二叉搜索树的基础特性（优势）

二叉搜索树的中序遍历结果是有序序列，因此天然支持范围查找 —— 这是其具备数据检索潜力的基础特性。

2. 二叉搜索树的核心缺陷

• 时间复杂度退化：若插入数据为有序序列，二叉搜索树会退化为 “单边树（斜树）”（如图左结构），此时查询、插入的时间复杂度从理想的 O (logN) 退化为 O (N)。
• 树高无法控制：节点数量增多时，树的高度会随数据分布大幅波动，无法维持稳定的层数。

3. 数据库场景下的致命问题

数据库数据存储在磁盘中，每访问一个子节点都会触发一次磁盘 IO—— 而磁盘 IO 的性能远低于内存操作，是数据库性能的核心瓶颈。若二叉搜索树高度失控（如退化为单边树），单次操作可能需要数十次甚至更多磁盘 IO，直接导致数据库性能急剧下降。

这也是数据库索引（如 MySQL InnoDB）选择 B + 树的核心原因：B + 树通过 “多叉结构” 严格控制树高，大幅减少磁盘 IO 次数，适配磁盘存储的特性。

3、N叉树

        为了解决树高的问题，我们可以使用N叉树

        通过观察，相同数据量的情况下，N叉树的树高可以得到有效的控制，也就意味着在相同数据量的情况下可以减少IO的次数，从而提升效率。但是MySQL认为N叉树做为索引的数据结构还不够好。

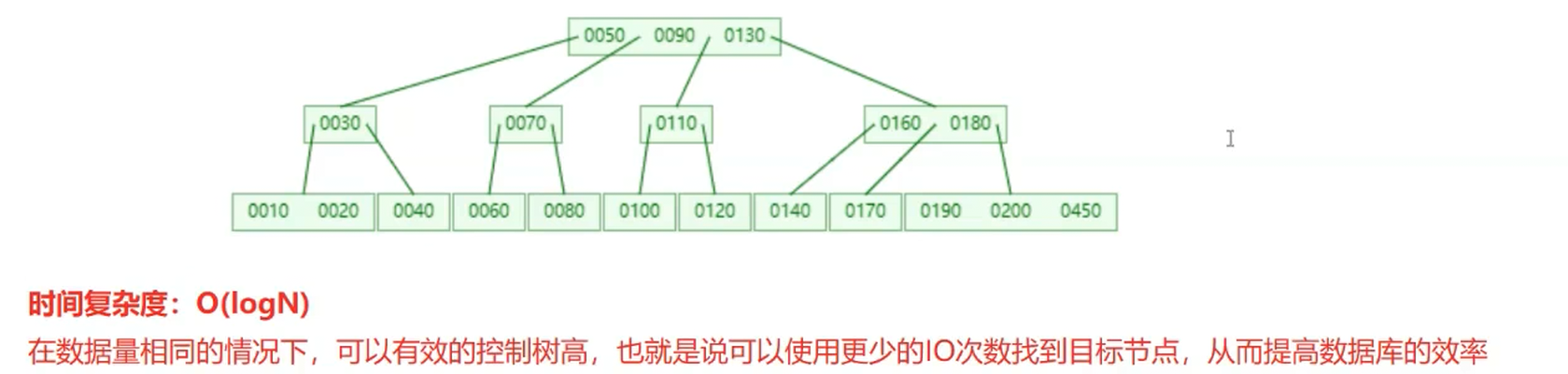
多叉树（数据库索引常用的 B/B + 树的基础结构）如何解决二叉树的树高问题，从而适配数据库的磁盘 IO 优化需求：

1. 多叉树的核心作用：控制树高

二叉树每个节点最多仅 2 个子节点，数据量增大时树高会急剧上升；而多叉树允许节点包含超过 2 个子节点，能在相同数据量下大幅降低树的高度，从根源上解决树高失控的问题。

2. “度（阶）” 的定义

“度” 是多叉树中节点的核心参数，指单个节点最多可拥有的子节点数：

• 图中选择 “Max. Degree = 4”，即每个节点最多有 4 个子节点；
• 节点的键数通常为 “度 - 1”（如图根节点包含 3 个键0050、0090、0130，对应 4 个子节点），实际子节点数一般小于度的值。

3. 性能优化：降低磁盘 IO 次数

多叉树的操作时间复杂度稳定为O(logN)（此处 log 的底数为节点的度）：在数据量相同的情况下，树高被严格压缩 —— 而数据库数据存储在磁盘中，树高越低，访问目标节点所需的磁盘 IO 次数越少，因此能大幅提升数据库的查询、插入效率。

4、B+树

4.1简介

        B树就是一种特殊的N叉搜索树， B+树是在B树的基础上通过“双向链表”把叶子节点串起来

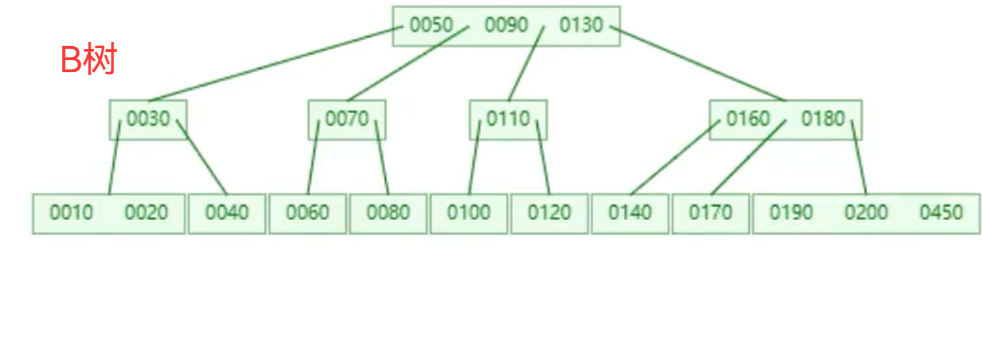
B 树是一种平衡的多叉搜索树，是数据库、文件系统等磁盘存储场景中常用的索引结构，核心特点是通过 “多叉平衡” 的设计，适配磁盘 IO 的性能特性

B 树是满足以下规则的多叉树（通常用 “度（阶）” 描述节点的子节点数量上限）：

• 设 B 树的度为m（即单个节点最多有m个子节点），则每个节点的键数介于⌈m/2⌉-1到m-1之间（保证树的平衡）；
• 节点的键值是有序的，且每个键对应一个子节点的区间（子节点的键值范围由父节点的键划分）；
• 叶节点处于同一层（平衡特性），保证任意操作的时间复杂度稳定为O(logₘN)（N为数据总量）。

特性：

• 多叉结构：单个节点可存储多个键和子节点指针，大幅降低树的高度；
• 平衡特性：插入、删除操作会通过 “节点分裂 / 合并” 维持树的平衡，避免树高失控；
• 有序性：节点内的键值有序排列，支持范围查找、精确查找等操作。

        B+树是⼀种经常用于数据库和文件系统等场合的平衡查找树，MySQL索引采用的数据结构，如下图所示：

在 B + 树中，节点分为非叶子节点（索引层节点）和叶子节点（数据层节点）

• 非叶子节点的作用是 “索引导航”，只存储 “键值”（比如数字、字符串等索引标识），但不存储实际数据；
• 叶子节点是存储数据的地方，会包含所有的键值（包括非叶子节点中出现过的所有键值），且每个键值都与实际数据（或数据的指针）绑定。

4.2B+树的特点

（1）能够保持数据稳定有序，插入与修改有较稳定的时间复杂度

（2）非叶子节点仅具有索引作用，不存储数据，所有叶子节点保真实数据

（3）所有叶子节点构成⼀个有序链表，可以按照key排序的次序依次遍历全部数据

4.3B+树与B树的对比

（1）叶子节点中的数据是连续的，且相互链接，便于区间查找和搜索。

（2）非叶子节点的值都包含在叶子节点中

（3）对于B+树而言，在相同树高的情况下，查找任一元素的时间复杂度都⼀样，性能均衡。

（4）N叉树高度更低

三、MySQL中的页

1、为什么要使用页

局部性原理： 是指程序在执行时呈现出局部性规律，在⼀段时间内，整个程序的执行 仅限于程序中的某⼀部分。相应地，执行所访问的存储空间也局限于某个内存区域，局部性通常有两种形式：时间局部性和空间局部性。 时间局部性（TemporalLocality）：如果⼀个信息项正在被访问，那么在近期它很可能还会被再次访问。 空间局部性（SpatialLocality）：将来要用到的信息⼤概率与正在使用的信息在空间地址上是临近的。

数据页：叶子节点,存储若干个数据行 索引页 ：非叶子节点, 只需要存储 key /子节点的位置

        每⼀个页中即使没有数据也会使用 16KB 的存储空间，同时与索引的B+树中的节点对应，查看页的大小，可以通过系统变量 innodb_page_size 查看

SHOW VARIABLES LIKE 'innodb_page_size';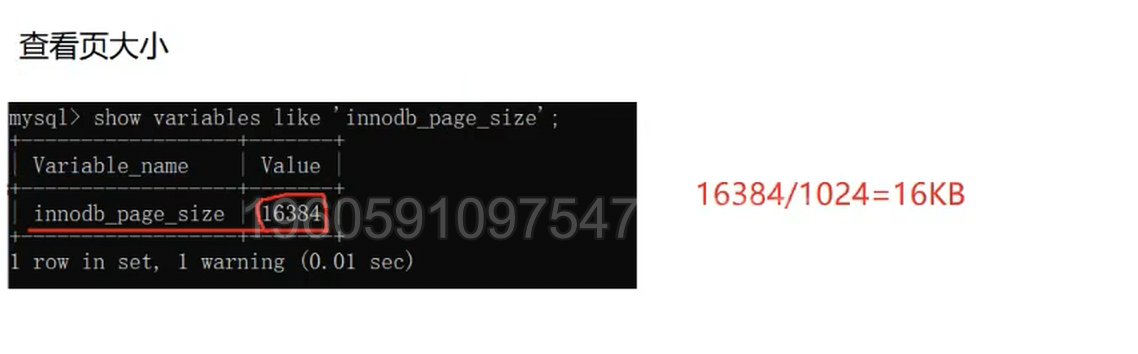

LInux 的操作系统中管理文件的大小最小的单位是4KB

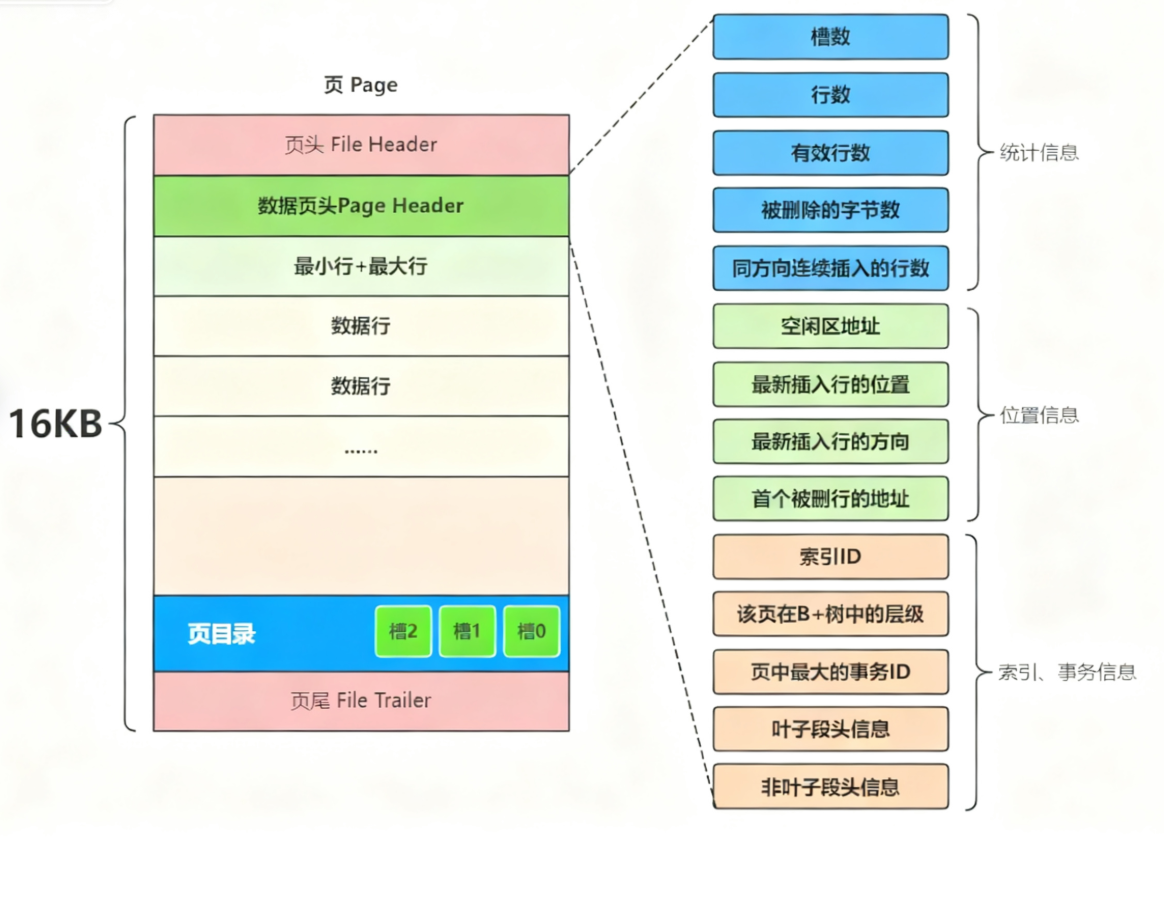
MySQL作为一个数据库程序，以4KB位单位区操作文件显然就是有点小了，所以我们定义以16KB一页的默认大小。         在MySQL中有多种不同类型的页，最常用的就是用来存储数据和索引的"索引页"，也叫做"数据页"，但不论哪种类型的页都会包含页头(FileHeader)和页尾(FileTrailer)，页的主体信息使用数 据"行"进行填充，数据页的基本结构如下图所示：

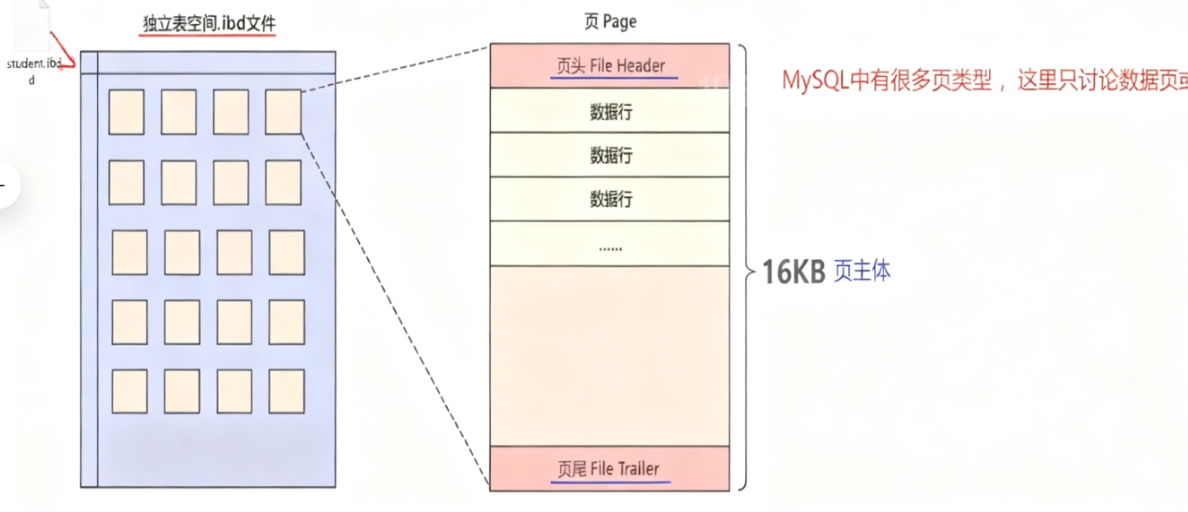
2、页文件头和页文件尾

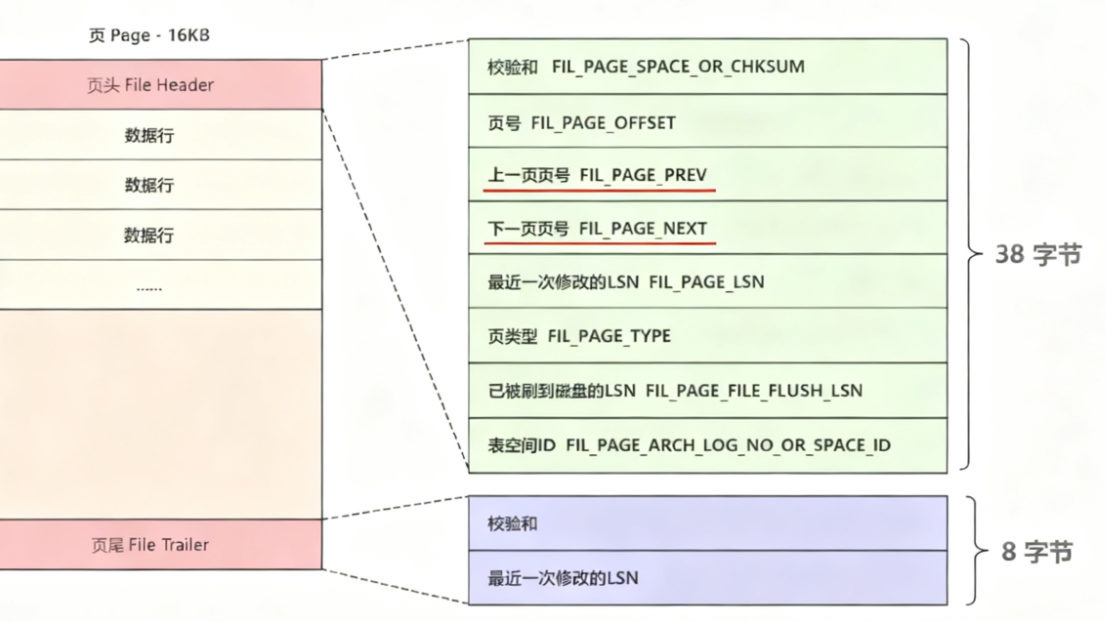
        页文件头和页文件尾中包含的信息，如下图所示：

        这⾥我们只关注，上⼀页页号和下⼀页页号，通过这两个属性可以把页与页之间链接起来，形成⼀个双向链表。

3、页主体

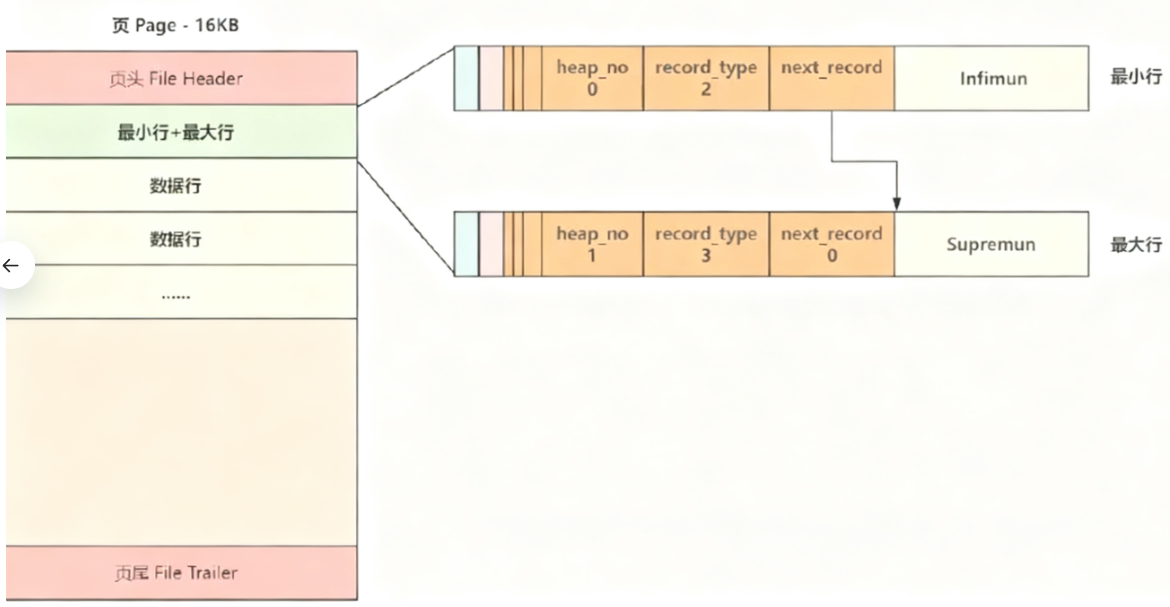
        当向⼀个新页插入数据时，将 Infimun 连接第⼀个数据行，最后⼀行真实数据行连接 Supremun ，这样数据行就构建成了⼀个单向链表，更多的行数据插入后，会按照主键从小到大 的顺序进行链接，如下图所示

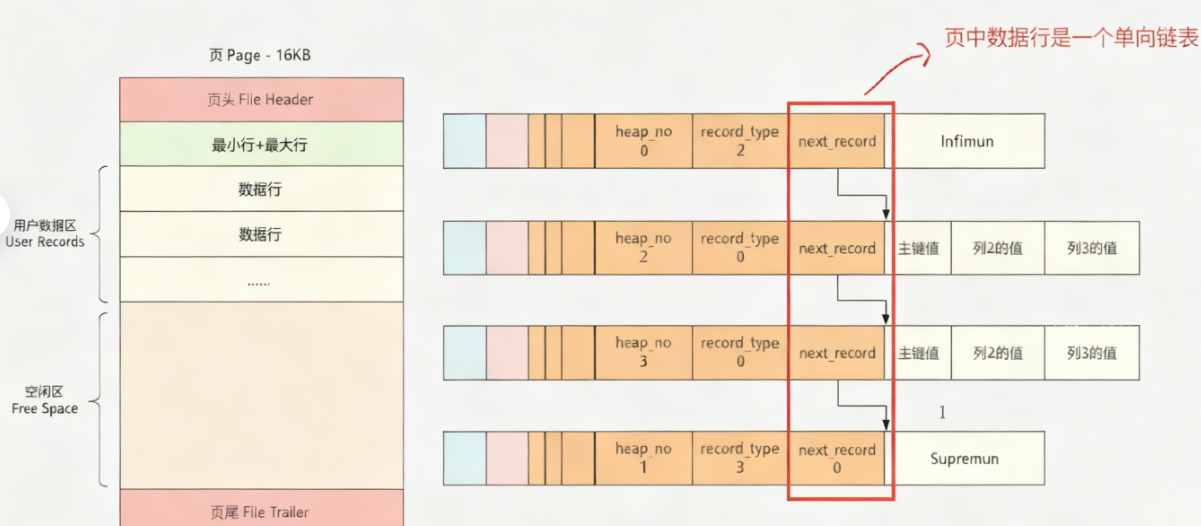
4、页目录

在 InnoDB 数据页中，“最小行（Infimum）” 和 “最大行（Supremum）” 的位置信息，记录的是它们相对于当前数据页起始位置的偏移量         当按主键或索引查找某条数据时，最直接简单的方法就是从头行 infimun 开始，沿着链表顺序逐个比对查找，但⼀个页有16KB，通常会存在数百行数据，每次都要遍历数百行，无法满足高效查 询，为了提高查询效率，InnoDB采用⼆分查找来解决查询效率问题；

        具体实现方式是，在每⼀个页中加入⼀个叫做页目录 Page Directory 的结构，将页内包括头 行、尾行在内的所有行进行分组，约定头行(最小行）单独为⼀组，其他每个组最多8条数据，同时把每个组 最后⼀行(最大行)在页中的地址放到最后一个组了，按主键从小到大的顺序记录在页目录中在，页目录中的每⼀个位置称为⼀ 个槽，每个槽都对应了⼀个分组，⼀旦分组中的数据行超过分组的上限8个时，就会分裂出⼀个新 的分组，槽里存的都是组里的最后一个。

        后续在查询某行时，就可以通过⼆分查找，先找到对应的槽，然后在槽内最多8个数据行中进行遍历即可，从而大幅提高了查询效率，这时⼀个页的核心结构就完成了；

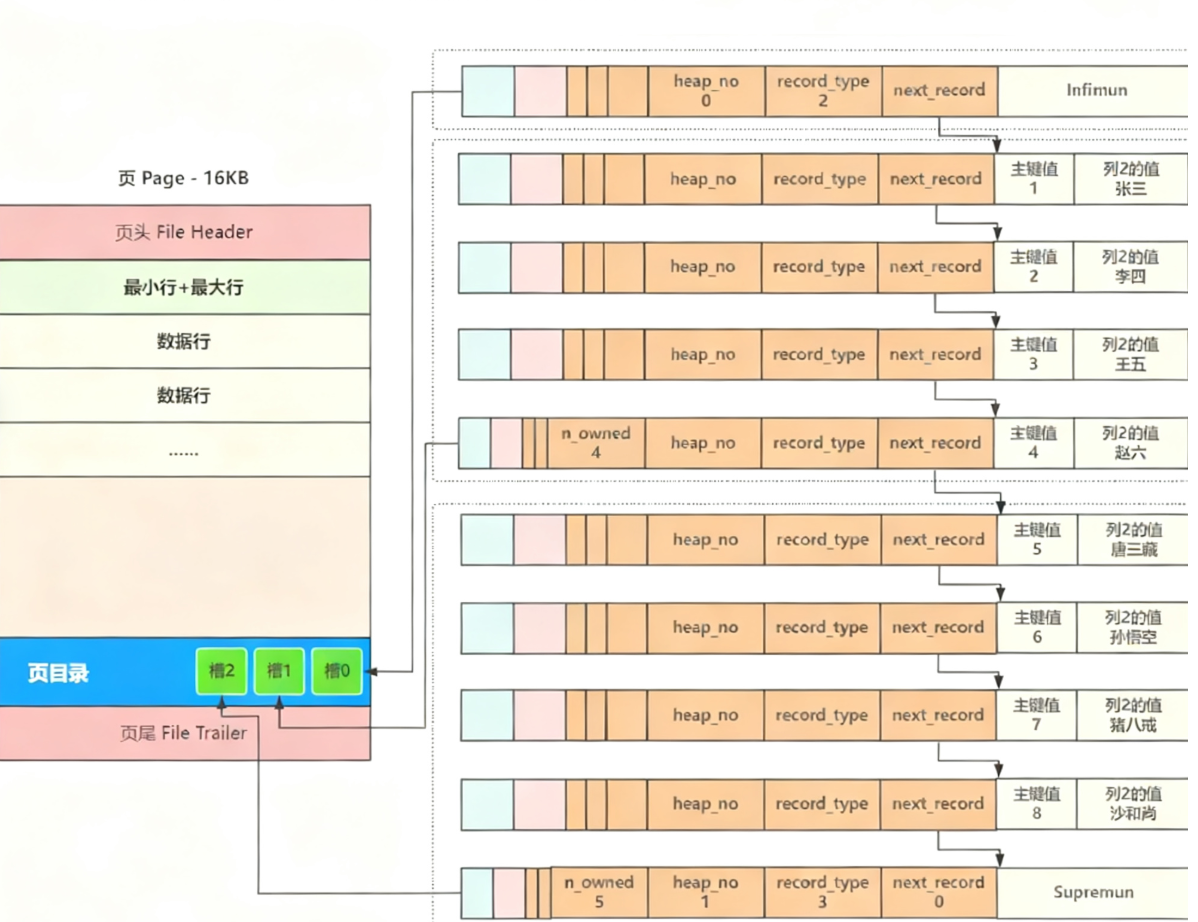
        例如要查找主键为6的行，先比对槽中记录的主键值，定位到最后⼀个槽2，再从最后⼀个槽中的第⼀条记录遍历，第⼆条记录就是我们要查询的目标行。

利用 “上一个槽的边界行”+“行的单向链表”，锁定目标分组的范围，再遍历分组内的行找到目标记录

第一步：二分查找页目录，确定 “目标槽”

第二步：通过 “上一个槽”，锁定分组的起始行

第三步：遍历分组内的行，找到目标记录

5、数据页头

        数据页头记录了当前页保存数据相关的信息，如下图所示

 五、B+在MySQL索引中的应用

        非叶子节点保存索引数据，叶子节点保存真实数据，如下图所示

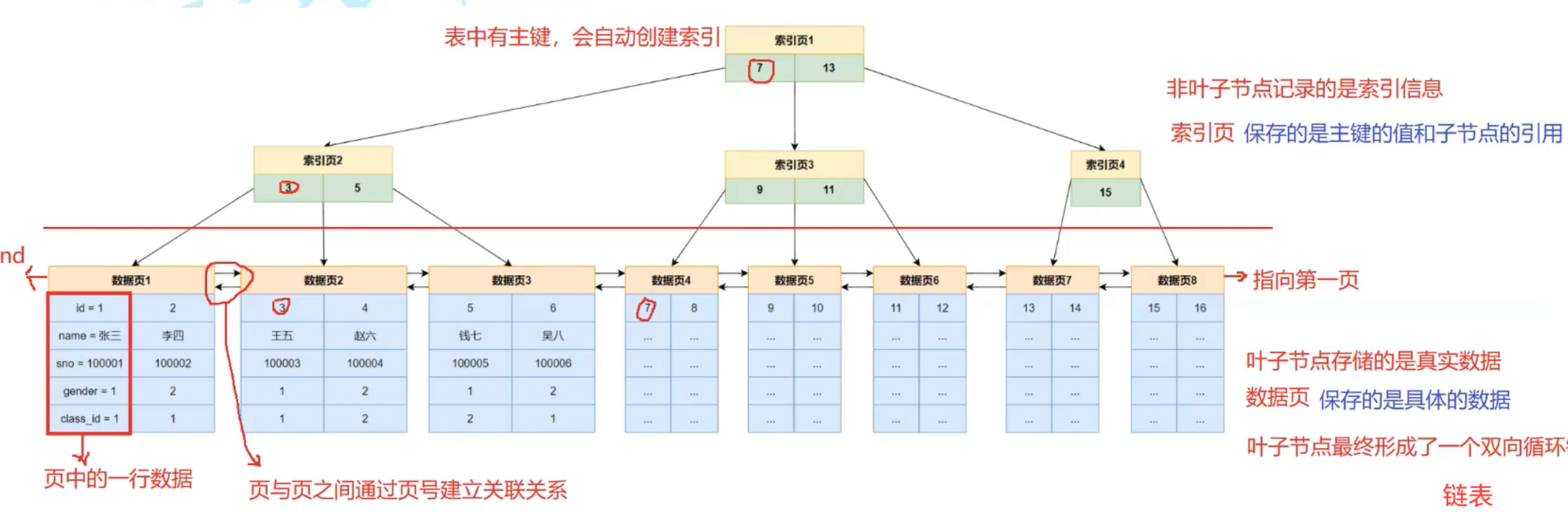
以查找id为5的记录，完整的检索过程如下：

        首先判断B+树的根节点中的索引记录，此时 5 < 7 ，应访问左孩子节点，找到索引页2

        在索引页2中判断id的大小，找到与5相等的记录，命中，加载对应的数据页

以上的IO过程，加载索引页1-->加载索引页2-->加载数据页3

• 第一步：先查根索引页（索引页 1），根页里的分界键是7、13→ 因为5 < 7，所以确定目标在 “左孩子节点（索引页 2）”；
• 第二步：查索引页 2，索引页 2 里的键是3、5→ 找到5对应的索引记录，这条记录直接关联了 “id=5 所在的数据页（数据页 3）” 的页号；
• 第三步：直接加载数据页 3，然后在数据页 3 内找到 id=5 的具体行。

注意：所有关于页的操作和访问都是在内存中进行的

1、计算三层树高的B+树可以存放多少条记录 （了解一些计算，要有一点基本的估算能力）

        假设⼀条用户数据大小为1KB，在忽略数据页中数据页自⾝属性空间占用的情况下，一页可以存16 条数据

        索引页一条数据的大小为，主键用BIGINT类型占8Byte，下一页地址6Byte，⼀共是14Byte，⼀个索引页可以保存 16*1024/14 = 1170 条索引记录

        如果只有三层树高的情况，综合只保存索引的根节点和⼆级节点的索引页以及保存真实数据的数据页，那么⼀共可以保存 1170*1170*16 = 21,902,400 条记录，也就是说在两千多万条数据的 表中，可以通过三次IO就完成数据的检索

1. 索引页的基本信息

• 索引页大小：图中索引页是16KB（这是 InnoDB 默认的页大小，所有数据 / 索引都以 “页” 为单位存储）。
• 索引页的内容：索引页（非叶子节点）存的是 **“主键值 + 子节点引用”**：
  • 主键值：这里用的是bigint类型（MySQL 中 bigint 占 8 字节），用来做范围分界；
  • 子节点引用：指向下一个节点（下一层索引页 / 数据页）的地址（偏移量），占 6 字节；
  • 所以一条索引记录的大小是：8字节（主键） + 6字节（地址）= 14字节。

2. 单个索引页能存多少条索引记录？

索引页总大小是16KB = 16 × 1024 字节 = 16384字节，用总字节数除以单条索引记录的大小，得到：16384 ÷ 14 ≈ 1170条→ 一个索引页（非叶子节点），理论上能存约 1170 条 “主键 + 子节点地址” 的索引记录。

3. 三层 B + 树的总存储容量

B + 树是 “层级式” 结构，三层 B + 树的结构是：

• 第 1 层（根节点）：1 个索引页，能存 1170 条索引记录 → 对应1170 个第 2 层的索引页；
• 第 2 层（中间索引层）：每个索引页也能存 1170 条记录 → 每个第 2 层索引页对应1170 个第 3 层的数据页；
• 第 3 层（叶子节点）：这里假设每个数据页能存16条实际记录（实际数据页存多少，取决于每行数据的大小；图中是举例子用 16）。

所以总记录数 = 第 1 层对应第 2 层的数量 × 第 2 层对应第 3 层的数量 × 每个数据页的记录数：1170 × 1170 × 16 = 21902400条（约 2190 万条）

六、索引分类

1、主键索引

        当在⼀个表上定义⼀个主键 PRIMARY KEY 时，InnoDB使用它作为聚集索引。

        推荐为每个表定义⼀个主键。如果没有逻辑上唯一且非空的列或列集可以使用主键，则添加⼀个自增列。

1. 主键索引
   • 当你在数据库中创建一个主键（Primary Key） 时，数据库会自动为主键列创建一个索引。
   • 这个索引的值就是主键列的值。
2. 建议每个表都定义一个主键
   • 如果没有逻辑上唯一且非空的列或列集适合作为主键，可以添加一个自增列（如自增ID） 作为主键。

2、普通索引

        最基本的索引类型，没有唯⼀性的限制。

        可能为多列创建组合索引，称为复合索引或组全索引

1. 最基本的索引类型：
   • 没有唯一性限制：允许列中存在重复值。
   • 可以为单个列或多个列创建。
2. 组合索引（复合索引/联合索引）：
   • 当索引包含多个列时，称为组合索引或复合索引。
   • 查询时遵循最左前缀原则，即查询条件必须从索引的最左列开始，才能有效利用索引。

3、唯一索引

        当在⼀个表上定义⼀个唯⼀键 UNQUE 时，自动创建唯⼀索引。

        与普通索引类似，但区别在于唯⼀索引的列不允许有重复值。

4、全文索引

        基于文本列(CHAR、VARCHAR或TEXT列)上创建，以加快对这些列中包含的数据查询和DML操作

        用于全文搜索，仅MyISAM和InnoDB引擎支持。

作用

• 在文本类型列（CHAR、VARCHAR、TEXT）上创建，用于加速文本内容的查询与全文搜索。
• 支持对文本数据进行关键词搜索、语义匹配等复杂查询，而不仅仅是简单的等值或范围查询。

支持引擎

• 在 MySQL 中，全文索引最初仅支持 MyISAM 存储引擎。
• 从 MySQL 5.6 版本开始，InnoDB 引擎也支持全文索引

🛠 使用场景

• 文章内容的关键词搜索
• 商品描述搜索
• 日志内容检索
• 任何需要模糊匹配或语义搜索的文本字段

使用方式：

-- 创建全文索引
CREATE FULLTEXT INDEX idx_content ON articles(content);

-- 使用全文索引查询
SELECT * FROM articles 
WHERE MATCH(content) AGAINST('数据库 索引');

5、聚集索引

聚集索引的选择规则（InnoDB）

1. 如果定义了 PRIMARY KEY，则主键索引就是聚集索引。
2. 如果没有主键，InnoDB 会选择第一个 UNIQUE 且 NOT NULL 的列作为聚集索引。
3. 如果既没有主键也没有合适的唯一索引，InnoDB 会自动创建一个隐藏的 ROW_ID 列（6 字节），作为聚集索引，该值单调递增。

隐藏的 ROW_I

• 是一个隐藏列，用户不可见。
• 占用 6 字节（用户原文中“G字节”可能是笔误）。
• 单调递增，类似于自增 ID，用于唯一标识一行。
• 仅在没有主键和唯一索引的情况下才会使用。

聚集索引的特点

• 叶节点直接存储数据行（而非指针），因此按聚集索引查询非常快。
• 数据行的物理顺序与聚集索引的逻辑顺序一致。
• 聚集索引可以保证行的唯一性（无论是主键、唯一索引还是 ROW_ID）。

聚集索引 vs 非聚集索引

• 聚集索引：数据行存储在索引的叶节点上，一个表只有一个。
• 非聚集索引：索引的叶节点存储的是主键值（或 ROW_ID），而非数据行本身，查询时需要回表。

最佳实践建议

• 推荐为每个表显式定义主键，最好使用自增整型，这样插入效率高，且能减少页分裂。
• 如果没有业务主键，也应添加一个代理主键（如 AUTO_INCREMENT），以便 InnoDB 能高效组织数据存储。

6、非聚集索引

• 聚集索引以外的索引称为⾮聚集索引或⼆级索引 ROW_ID 做为索引。

• ⼆级索引中的每条记录都包含该⾏的主键列，以及⼆级索引指定的列。

• InnoDB使用这个主键值来搜索聚集索引中的行，这个过程称为回表查询

定义

• 除聚集索引外的所有索引都称为非聚集索引或二级索引。
• 一个表可以有多个非聚集索引，用于加速基于不同列的查询。

二级索引的结构

二级索引的叶子节点存储的是：

• 该行的主键值（或 InnoDB 在没有主键时使用的 ROW_ID）
• 二级索引列本身的值

例如，如果在 name 列上创建二级索引，索引结构大致如下：

索引键（name值） -> 主键值

回表查询（Bookmark Lookup）

• 当通过二级索引查询时，InnoDB 会先在二级索引中找到对应的主键值，再用这个主键值去聚集索引中查找完整的数据行。
• 这个过程称为回表查询，意味着需要两次索引查找才能获取完整数据。

示例说明

假设有一个 users 表，结构如下：

CREATE TABLE users (
    id INT PRIMARY KEY,          -- 聚集索引
    name VARCHAR(50),
    age INT,
    INDEX idx_name (name)        -- 二级索引
);

执行以下查询：

SELECT * FROM users WHERE name = 'Alice';

查询过程：

1. 在二级索引 idx_name 中查找 name = 'Alice' 的记录，得到对应的 id 值。
2. 使用得到的 id 值，在聚集索引（主键索引）中查找完整的行数据。
3. 返回结果。

性能影响与优化

• 回表查询可能导致额外 I/O，尤其是当二级索引匹配的行很多时。
• 覆盖索引（Covering Index） 可以避免回表：
  • 如果查询的列全部包含在二级索引中，则无需回表。
  • 例如：SELECT id, name FROM users WHERE name = 'Alice'; 只需访问二级索引 idx_name。

二级索引的最佳实践

1. 选择性高的列适合创建二级索引（即重复值少的列）。
2. 避免过多二级索引，因为每个索引都会增加写操作的开销。
3. 考虑创建复合二级索引来覆盖常见查询，减少回表。

举例子：

非聚集索引查询过程（以 SELECT * FROM table WHERE name = '张三' 为例）

第 1 步：在二级索引树中查找

• 数据库会先去 name 列建立的非聚集索引树中查找 name = '张三' 的记录。
• 找到叶子节点后，会得到对应的 主键值（比如 id = 1001）。
• 这个过程很快，因为索引树是排序的，类似于查字典。

第 2 步：回表查询（回到聚集索引树）

• 数据库拿到 id = 1001 后，会去 主键索引树（聚集索引） 中查找 id = 1001 对应的完整数据行。
• 因为聚集索引的叶子节点存储的是整行数据，所以可以获取到所有列的值。
• 最后返回完整的查询结果。

为什么要这样设计？

• 非聚集索引只存储索引列 + 主键值，不存储完整数据，因此索引树更小、更快。
• 通过主键值作为“指针”回表查找，既能保证查询效率，又能节省存储空间。

组合索引的最匹配的原则：

1. 组合索引的结构与 “最左匹配原则”

这里的组合索引是按(name, sn)的顺序创建的（name为索引最左列，sn为后续列）。组合索引的生效规则是 “最左匹配原则”：

• 组合索引的索引树是先按最左列（name）排序，再按后续列（sn）排序；
• 查询条件需从索引的最左列开始匹配，才能触发索引；若跳过最左列直接使用后续列，索引无法利用其有序性，会失效。

2. 当前查询的索引生效情况

查询语句是select name from student where sn = '100002';：

• 该查询仅使用了组合索引的 ** 非最左列（sn）** 作为条件，未使用最左列（name）；
• 按照最左匹配原则，这个(name, sn)的组合索引不会生效（即不走该组合索引），数据库无法通过该索引定位数据，会触发全表扫描（或走其他针对 sn 的独立索引，若存在）。

3. 解决方案

若需让sn作为查询条件时生效，需为 sn 单独创建独立索引，而非依赖(name, sn)的组合索引。

7、索引覆盖

        当⼀个select语句使用了普通索引且查询列表中的列刚好是创建普通索引时的所有或部分列，这时就可以直接返回数据，而不用回表查询，这样的现象称为索引覆盖

注意：创建一个索引就会生成一个索引树，生成多少个索引就会生成多少个索引树

B+树的层次是否是固定的？

数据库中 B + 树的层数并非固定值，而是由数据量、索引记录大小、数据库页大小共同决定，实际应用中通常为 2~4 层：

1. B + 树层数的核心影响因素

以 InnoDB（默认页大小 16KB）为例：

• 索引页容量：InnoDB 索引页默认 16KB，若主键为bigint（8 字节）+ 子节点引用（6 字节），单条索引记录占 14 字节，单个索引页可存约 16×1024÷14≈1170条 索引记录（即 “扇出数” 约 1170）。
• 数据量：B + 树的扇出数决定了每层能覆盖的数据量：
  • 2 层 B + 树：1170 × 单数据页记录数（若单数据页存 16 条，可覆盖约 1.87 万条）；
  • 3 层 B + 树：1170×1170 × 单数据页记录数（约 2190 万条）；
  • 4 层 B + 树：1170×1170×1170 × 单数据页记录数（约 256 亿条）。

2. 实际应用中的层数范围

• 小数据量（万级以内）：B + 树通常为 2 层（根节点 + 数据页）；
• 中大数据量（千万～亿级）：B + 树多为 3 层（根节点 + 中间索引页 + 数据页）；
• 超大数据量（十亿级以上）：B + 树可能扩展到 4 层，但极少超过 4 层（因扇出数大，层数增长极慢）。

3. 层数的核心作用：控制磁盘 IO 次数

B + 树的层数直接对应 “查询时需要访问的磁盘页数量”：

• 3 层 B + 树查询仅需 3 次磁盘 IO（根页→中间索引页→数据页），而磁盘 IO 是数据库性能瓶颈之一，因此数据库会通过 “大页容量 + 高扇出数”，将 B + 树层数控制在 2~4 层，保证查询效率。

1. 组合索引的结构与 “最左匹配原则”

这里的组合索引是按(name, sn)的顺序创建的（name为索引最左列，sn为后续列）。组合索引的生效规则是 “最左匹配原则”：

• 组合索引的索引树是先按最左列（name）排序，再按后续列（sn）排序；
• 查询条件需从索引的最左列开始匹配，才能触发索引；若跳过最左列直接使用后续列，索引无法利用其有序性，会失效。

2. 当前查询的索引生效情况

查询语句是select name from student where sn = '100002';：

• 该查询仅使用了组合索引的 ** 非最左列（sn）** 作为条件，未使用最左列（name）；
• 按照最左匹配原则，这个(name, sn)的组合索引不会生效（即不走该组合索引），数据库无法通过该索引定位数据，会触发全表扫描（或走其他针对 sn 的独立索引，若存在）。

3. 解决方案

若需让sn作为查询条件时生效，需为 sn 单独创建独立索引，而非依赖(name, sn)的组合索引。

推荐自增整型，减少页分裂？

 InnoDB 的 “数据存储规则” 和 “自增主键的特性” 完美匹配，从而减少性能损耗。

第一步：先铺垫 2 个关键前提（InnoDB 的存储规则）

1. 数据按 “页” 存储：InnoDB 把数据分成一个个 “数据页”（默认 16KB），所有行数据都存在页里，页满了就需要新页；
2. 数据按 “主键顺序排序”：因为主键是聚集索引，数据页内的行、甚至不同数据页之间，都会按主键从小到大 “有序排列”（比如页 1 存主键 1~16，页 2 存 17~32，依次递增）。

第二步：什么是 “页分裂”？（性能杀手）

当插入数据时，若新数据的主键值 “插在两个已有主键中间”，且目标数据页已经满了，InnoDB 就必须做一件 “费力的事”——页分裂：

1. 先创建一个新的空数据页；
2. 把原数据页中 “大于新主键” 的部分数据，移动到新页；
3. 把新数据插入到原页的对应位置；
4. 更新索引（页目录、B + 树的节点引用），确保排序顺序不变。

举个反例（非自增主键）：

• 现有数据页 1 已满，存的主键是 [10,20,30,...,90]（假设每页存 9 条）；
• 现在插入主键 = 15 的新数据（插在 10 和 20 之间）；
• 页 1 已没空间，必须触发 “页分裂”：新建页 2，把页 1 中 [20,30,...,90] 移到页 2，再把 15 插入页 1，最后更新索引指向。

页分裂的危害：

• 消耗 CPU/IO：拆页、移动数据、更新索引都是 “重量级操作”，插入效率骤降；
• 产生碎片：分裂后原页和新页都可能没存满（比如页 1 只剩 [10,15]），页利用率变低，后续查询需要扫描更多页，性能变差。

数据页1：[10, 15]          (2条记录，有7个空位) 数据页2：[20,30,40,50,60,70,80,90]  (8条记录，有1个空位)

第三步：自增整型为什么能 “减少页分裂”？

自增整型主键（比如 id INT AUTO_INCREMENT）的核心特性是：插入的新主键值永远是 “当前最大的”（比如之前最大是 90，新插入就是 91，再插是 92）。

结合 InnoDB 的 “按主键排序” 规则，这种特性会导致：

• 新数据永远 “追加在最后”：不管是当前数据页（没满时），还是新数据页（当前页满了时），新行永远插在 “所有已有数据的后面”，不会插在中间；
• 完全避免 “中间插入”：既然不会插在两个已有主键之间，自然就不会触发 “页分裂”—— 除非当前页满了，直接新建一个页，把新数据追加进去（这个过程叫 “页扩展”，比页分裂简单 10 倍，几乎无性能损耗）。

InnoDB实际的页分裂策略详解

📌 InnoDB页分裂的核心设计原则

1. 填充因子（Fill Factor）

• InnoDB页默认填充率约为15/16（93.75%）
• 当页使用率达到93.75%时触发分裂，而不是100%
• 保留1/16（6.25%） 的空间用于后续更新和插入

2. 分裂目标：50/50平衡分裂

InnoDB实际采用更智能的分裂策略：

原始页：[10,20,30,40,50,60,70,80,90] (已满)
插入：35（应插在30和40之间）

实际分裂过程：
1. 找到中间点：通常是页的中间位置
2. 创建新页（页2）
3. 将约一半数据移到新页（如[60,70,80,90]）
4. 原页保留[10,20,30,40,50]
5. 插入35到原页：[10,20,30,35,40,50]

结果：
页1：[10,20,30,35,40,50]  (6条，约66%填充)
页2：[60,70,80,90]        (4条，约44%填充)

分裂点选择策略：

1. 中间分裂（默认）：选择页中间位置
2. 适应插入点：考虑新记录位置，尽量均衡
3. 考虑记录大小：按字节数均衡，不只是记录数

InnoDB的优化机制

1. 自适应哈希索引

• 监控频繁访问模式
• 对热点数据建立内存哈希索引
• 减少分裂时的索引查找开销

2. 插入缓冲（Insert Buffer）

• 对非唯一二级索引的插入进行缓冲
• 减少随机I/O，提高插入性能
• 延迟索引更新，减少分裂时的锁竞争

3. 页合并（Page Merge）

• 当页删除记录导致填充率过低（<50%）时
• 尝试与相邻页合并
• 保持空间利用率，减少碎片

4. 空间预留

-- InnoDB的填充因子配置
-- 默认PAGE_FILL_FACTOR = 15/16 = 93.75%
-- 保留6.25%空间用于更新

优势：

• 减少因UPDATE导致的行溢出
• 为后续插入预留空间
• 降低分裂频率

详细的分裂点选择策略：

1. 中间分裂（默认策略）：按 “记录数” 找中间位置，追求 “简单稳定”

分裂点选择方式：

不考虑新插入记录的位置、不考虑每条记录的大小，仅按 原页中记录的 “条数” 找中间值 —— 比如原页有 N 条记录，分裂点就是第「N/2」条记录（向下取整或向上取整，由 InnoDB 内部逻辑决定）。

核心目的：

实现 “最简单的均衡”，避免代码逻辑复杂，保证分裂过程的稳定性（默认优先保证 “不出错”，再考虑优化）。

例子：

原页（16KB）存 8 条记录（主键 10、20、30、40、50、60、70、80），每条记录大小相近（假设均为 1KB）：

• 按中间分裂，分裂点是第 4 条记录（主键 40）；
• 原页保留：10、20、30、40（4 条）；
• 新页迁移：50、60、70、80（4 条）；
• 新插入记录（比如主键 45）：插入原页末尾（原页剩余空间足够），无需再次分裂。
• 插入新纪录是(55),就插入新页50的后面

优点 & 缺点：

• 优点：逻辑简单，分裂速度快，原页和新页的 “记录数” 完全均衡；
• 缺点：忽略插入场景和记录大小，可能导致后续频繁分裂 —— 比如频繁在某一侧插入（如总插小于 40 的记录），原页很快又满，再次触发分裂。

2. 适应插入点：围绕 “新插入记录的位置” 选分裂点，减少后续分裂

分裂点选择方式：

优先考虑新插入记录的位置，把分裂点设在 “插入点附近”，让新插入记录所在的一侧（原页或新页）预留更多空间，避免短期内再次触发分裂。

核心目的：

针对性优化 “频繁在同一区间插入” 的场景（比如非自增主键的中间插入），减少分裂次数。

例子：

原页存 8 条记录（10、20、30、40、50、60、70、80），现在要插入主键 15（插入点在 10 和 20 之间），触发页分裂：

• 按 “适应插入点” 策略，分裂点会选在插入点右侧（比如主键 20），而非中间；
• 原页保留：10、15（新插入）、20、30（4 条，预留更多左侧空间）；
• 新页迁移：40、50、60、70、80（5 条）；
• 后续再插入 12、18 等记录：可直接插入原页，无需再次分裂（解决了 “中间分裂” 的痛点）。

优点 & 缺点：

• 优点：贴合实际插入场景，减少同一区间的频繁分裂，插入效率更高；
• 缺点：记录数可能不均衡（如例子中原页 4 条、新页 5 条），但牺牲 “条数均衡” 换 “更少分裂”，性价比更高。

3. 考虑记录大小：按 “字节数” 均衡，而非 “记录数”，提升空间利用率

分裂点选择方式：

不按 “记录条数” 划分，而是计算原页中所有记录的 总字节数，找到 “总字节数的中间位置” 作为分裂点 —— 确保原页和新页的 “占用字节数” 接近，而非 “记录数” 接近。

核心目的：

解决 “记录大小差异大” 的问题（比如表中有大字段 VARCHAR、TEXT），避免按条数分裂导致的 “空间浪费” 或 “一侧过载”。

例子：

原页（16KB）存 5 条记录，记录大小差异大（单位：KB）：

• 记录 1（主键 10）：6KB（含大字段）；
• 记录 2（主键 20）：1KB；
• 记录 3（主键 30）：1KB；
• 记录 4（主键 40）：1KB；
• 记录 5（主键 50）：6KB（含大字段）；总字节数 = 6+1+1+1+6=15KB（接近 16KB 满），现在插入新记录（主键 25，1KB），触发分裂：

若按 “中间分裂”（按条数）：

分裂点是第 3 条（主键 30），原页留 10、20、25（新插入）→ 总字节数 = 6+1+1=8KB；新页留 30、40、50→ 总字节数 = 1+1+6=8KB（看似均衡，但实际记录大小差异被忽略，无问题）。

若记录大小更极端（比如记录 1=10KB，其他 4 条各 1KB，总 14KB）：

• 按 “中间分裂”（条数）：分裂点第 3 条（主键 30），原页留 10、20、25→ 字节数 = 10+1+1=12KB（接近 16KB 上限），后续再插小记录可能很快满；新页留 30、40、50→ 字节数 = 1+1+1=3KB（严重浪费空间）；
• 按 “考虑记录大小” 策略：总字节数 14KB，分裂点找 “7KB 左右” 的位置：记录 1（10KB）已超过 7KB，所以分裂点设为记录 1 之后；原页留 10（10KB），新页留 20、25（新插入）、30、40、50（总字节数 = 1+1+1+1+1=5KB）；原页剩余 6KB，新页剩余 11KB，空间利用率更均衡，后续插入更灵活。

优点 & 缺点：

• 优点：避免 “大记录扎堆” 导致的空间不均衡，提升数据页的整体空间利用率；
• 缺点：需要计算每条记录的字节数，分裂逻辑比 “中间分裂” 复杂，分裂速度略慢。

总结: