【算法精讲】一篇让你掌握前缀和算法（附图解和不少题目练习~~）

用户11935701

发布于 2025-12-16 08:40:08

1640

1.简介

前缀和算法是一种用空间换时间的算法，他常常用于解决某些题目或者作为某些高级算法的组成部分。

例如：让你求某个矩阵（一维）的子矩阵的最大值，如果使用暴力解法它的时间复杂度将会是O(n^2) ，但如果使用该算法就可以使其时间复杂度降低一个维度也就是O(N).

2.一维前缀和

讲解

该算法需要开辟一个比原数组的大小大一个内存的数组

它的每一个元素意义是：前原数组n个元素的总和。也就是说下标为3的元素，是原来前三个元素的和。（也可以理解为除了自己以外的前面元素的和）

至于为什么会多开辟一个元素，我们后续会讲。

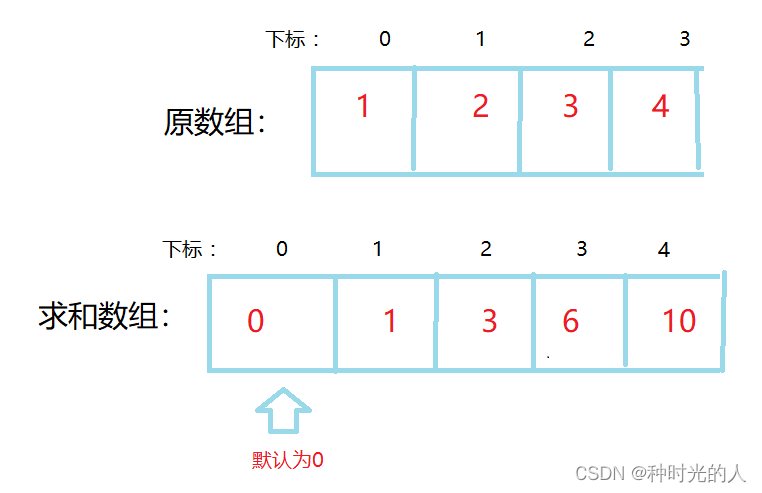
因此我们可以得出求和数组的递推公式：

sum[i]=arr[i-1] + sum[i-1]

此时我们多开一个内存的意义就可以体现出来了，当我们求第一个元素数组的时候需要加上前一个sum 。

但是如果第一个元素前一个位置没有东西就会发生越界访问，因此我们要给他提前准备一个内存并且默认为0。

总的来说，就是为了处理第一个元素越界的问题。

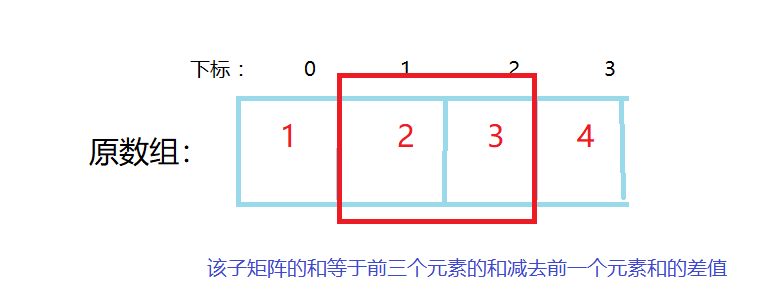
求子矩阵内的和

我们已经知道了sum的每一个元素的意义，那么原数组的子矩阵的和也就可以得出来，例如：下标x到y的子矩阵之和就等于：

son=sum[y+1]-sum[x]

代码

如果你理解了上述内容，它的代码就可以轻松写出来：

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int arr[5] = {1,2,3,4,5};
	int sum[6];
	sum[0] = 0;

	for (int i = 1; i < 6; i++) sum[i] = arr[i - 1] + sum[i - 1];

	for (auto i : sum) cout << i << ' ';
	
	return 0;
}

运行结果：

3.二维前缀和

讲解

二维前缀和相对于一维复杂的多，它也需要多开辟空间，不同的是他是在每个维度都要多开辟一个。

它每个元素的意义是：下标为(x,y)的求和数组的元素，是原数组下标（0,0）到（x - 1, y - 1）子矩阵内元素的和，建议配合图来理解。

举个例子： sum[2][2] = arr[0][0] + arr[0][1] + arr[1][0] + arr[1][1] 其他也是如此。

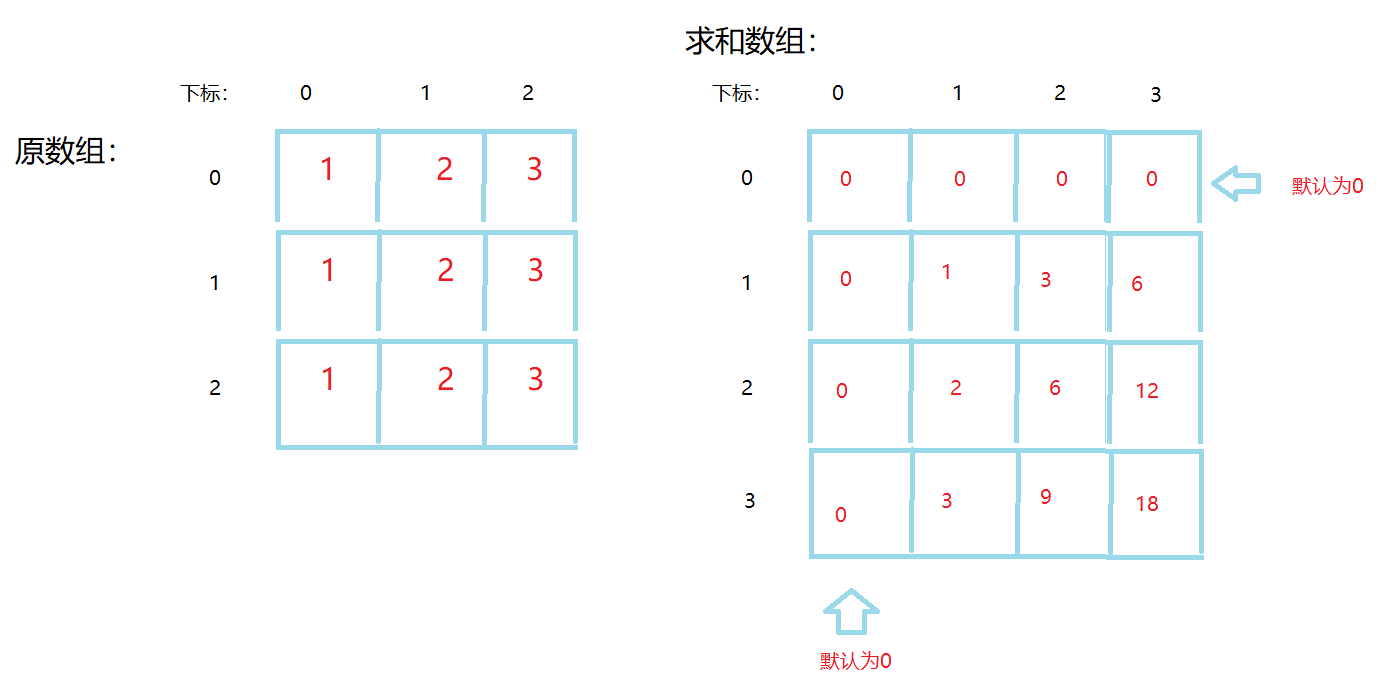
如果你理解了上述内容，那么就让我们来推一下它的递推公式：至于我们为什么要这么求，暂且往下看。

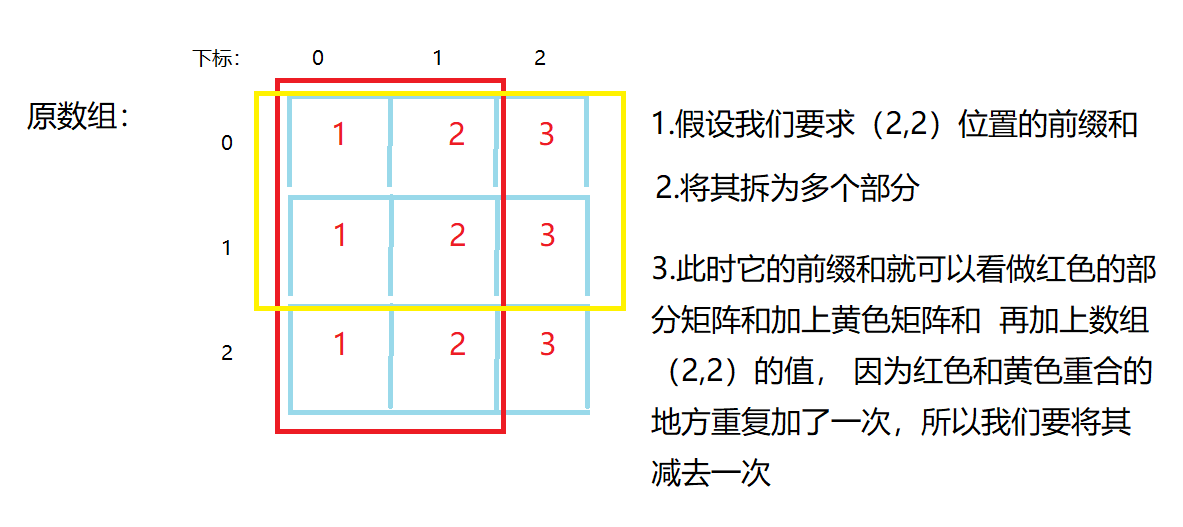
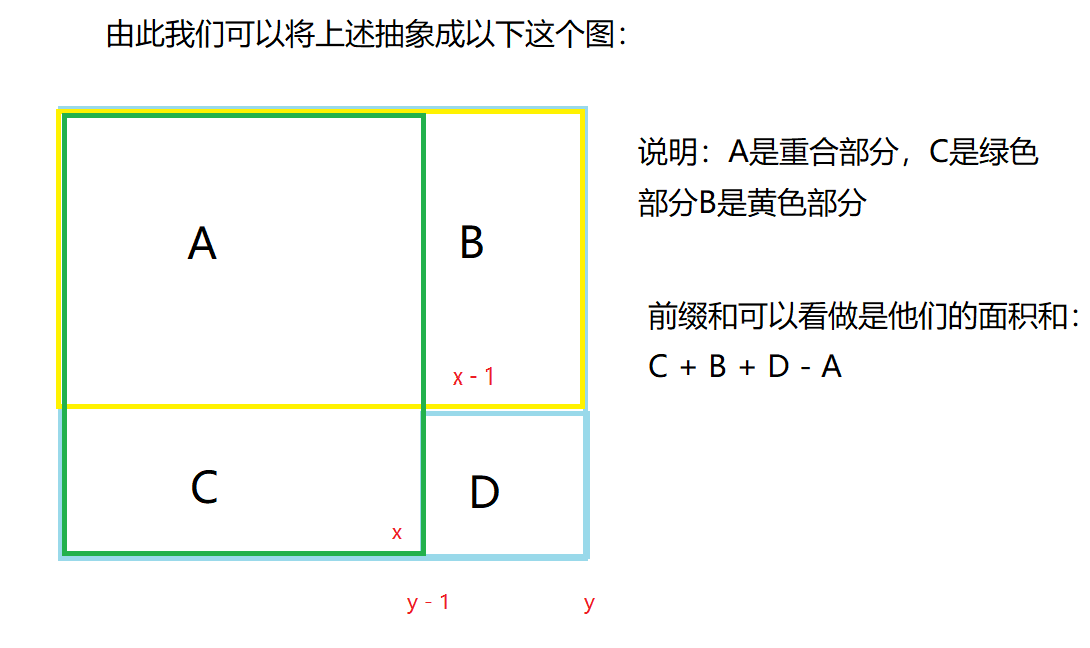
当我们求前缀和的时候，我们是顺序求取的，当我们求（x，y）位置的前缀和时候，我们的（x,y - 1），(x - 1, y -1)，(x- 1,y)这三个位置的前缀和就已经求出来了，也就是说ABCD的位置的值你都是知道的，所以我们我么可以得出以下公式：

sum[x][y] = sum[x-1][y] + sum[x][y-1] - sum[x-1][y-1] + arr[x- 1][y-1]

求子矩阵和

求子矩阵和是建立在已经求出所有前缀和基础上的，求子矩阵和的方法和求前缀和的方法相似，且看图解：

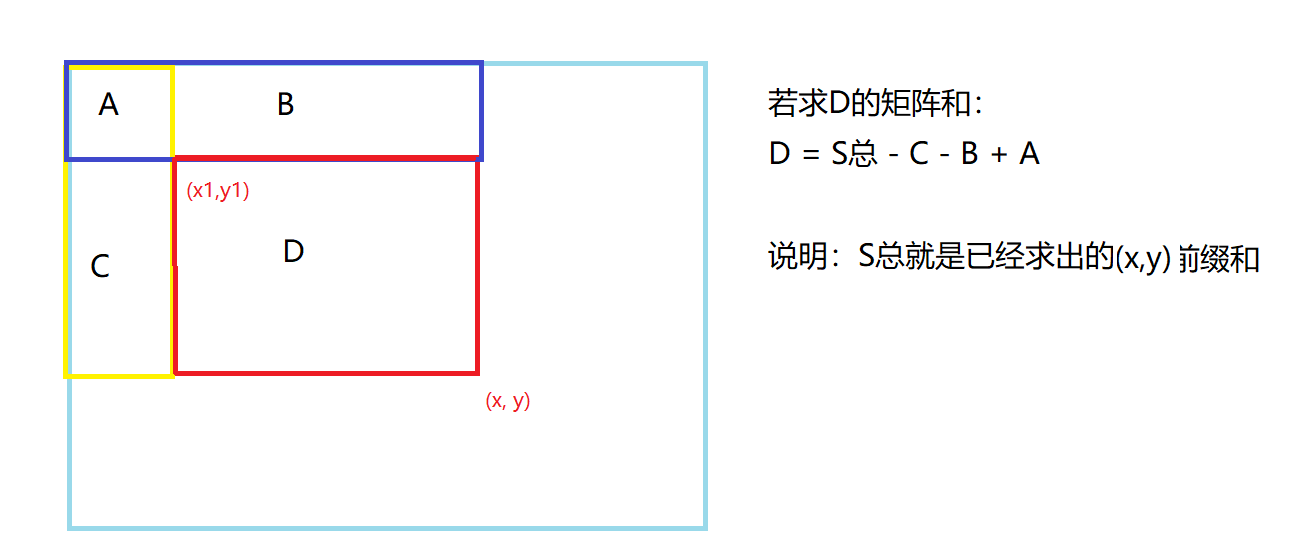
由此我们可以得出递推公式，原数组（x1,y1）到（x,y）的子矩阵：

son =sum[x+1][y+1] +sum[x1][y1]-sum[x+1][y1]-sum[x1][y+1]

代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
	vector<vector<int>>v(3, vector<int>(3));
	vector<vector<int>>sum(4, vector<int>(4, 0));

	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
		{
			v[i][j] = j + 1;//每个一维数组初始化为1 2 3
			sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + v[i][j];//递推
		}
	
	for (auto i : sum)
	{
		for (auto k : i)
			cout << k << ' ';
		cout << endl;
	}

	int x1, y1,x,y;

	cout << "子矩阵坐标：" << endl;
	cin >> x1 >> y1 >> x >> y;//求子矩阵
	cout << sum[x + 1][y + 1] - sum[x + 1][y1] - sum[x1][y + 1] + sum[x1][y1];

	return 0;
}

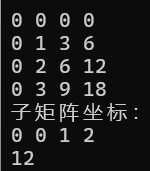
运行结果：

4.题目

一维前缀和模板

点这里进入答案：最简单的都不会？？？回去再翻翻去

二维前缀和模板

点这里进入答案：这个做对了说明你理解这个算法了

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main() {
    int n = 0, m = 0, q = 0;
    cin >> n >> m >> q;

    vector<vector<int>> arr(n + 1, vector<int>(m + 1));
    vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> arr[i][j];
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];
        }
    }
    int x1, y1, x2, y2;
    while (q--) {
        cin >> x1 >> y1 >> x2 >> y2;
        cout << dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1] <<
             endl;
    }
    return 0;
}

寻找数组的中心下标

点吧你，一点一个不吱声

思路：

前缀和+后缀和（这个纯属就是前缀的倒序版）
如果这个元素的前缀和和后缀和相同，说明找到了。

class Solution {
public:
    int pivotIndex(vector<int>& nums) {

        vector<int>dp(nums.size() + 1, 0);
        vector<int>dp1(nums.size() + 1, 0);

        for (int i = 1; i <= nums.size(); i++) {
            dp[i] = dp[i - 1] + nums[i - 1];
        }
        for(int i = nums.size() - 2; i >= 0; i--){
            dp1[i] = dp1[i + 1] + nums[i + 1];
        }

        for (int i = 0; i < nums.size(); i++) {
            if (dp[i] == dp1[i])
                return i;
        }

        return -1;
    }
};

除自己以外数组的乘积

点我就完事了思路：

前缀和算法的简单变化，本质依旧如此
可以使用上一个题的方法，前缀和+后缀和
下面的方法是那个方法的优化，空间复杂度优化到了O(1)

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
       // int sum = accumulate(nums.begin(), nums.end(), 1, mulltiplies<int>());
        int n = nums.size();
        vector<int> ans(n);
        ans[0] = 1;

        for(int i = 1; i < n;i++)
            ans[i] = ans[i - 1] * nums[i - 1];
        
        int r = 1;
        for(int i = n - 1; i >= 0;i--){
            ans[i] = ans[i] * r;
            r *= nums[i];
        }

        return ans;
    }
};

和为k的子数组

挺难的思路：

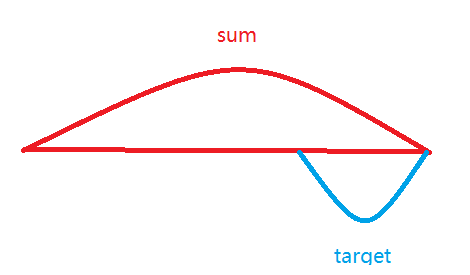
假设这个位置存在连续数组使其和为target，那么说明其前面的前缀和必存在sum - target的值
配合哈希表使用，记录前面每个前缀和出现的次数
从头开始遍历，一遍存前缀和，一边找是否有符合的数组

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> hash;
        int sum = 0;
        int ret = 0;

        for(auto i : nums)
        {
            hash[sum]++;
            sum += i;
            if(hash.count(sum - k)) ret += hash[sum - k];
        }
        return ret;
    }
};

感谢观众老爷的观看Thanks♪(･ω･)ﾉ，如果觉得满意的话留个关注再走吧。

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2024-04-01，如有侵权请联系 cloudcommunity@tencent.com 删除

int