【优选算法必刷100题】第025~26题（前缀和算法）：【模版】前缀和、【模板】二维前缀和

艾莉丝努力练剑

发布于 2025-11-18 13:30:34

1080

文章被收录于专栏：C / C++C / C++

025 【模板】一维前缀和

牛客网链接：DP34 【模板】前缀和

题目描述：

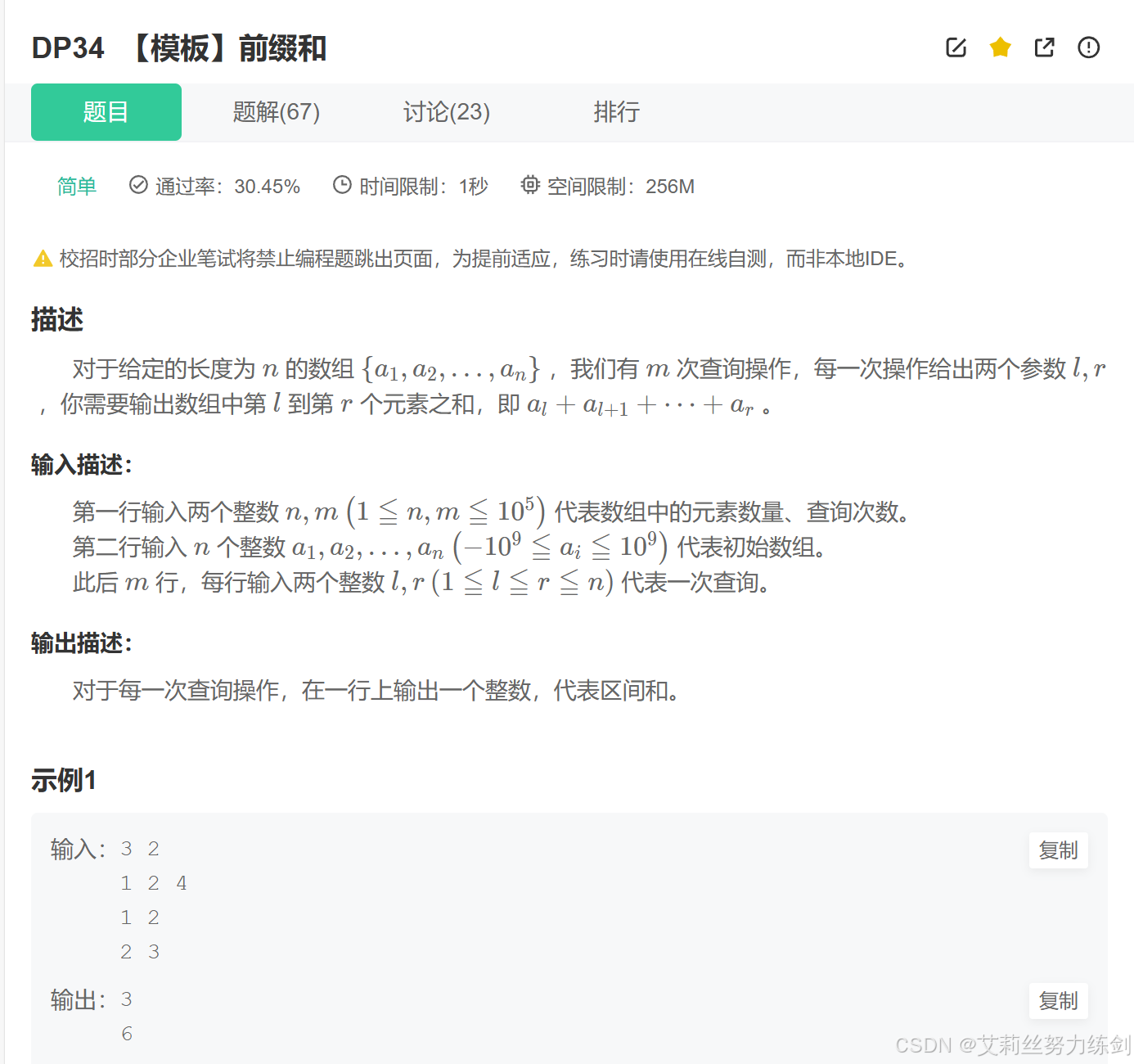
1.1 算法思路：前缀和

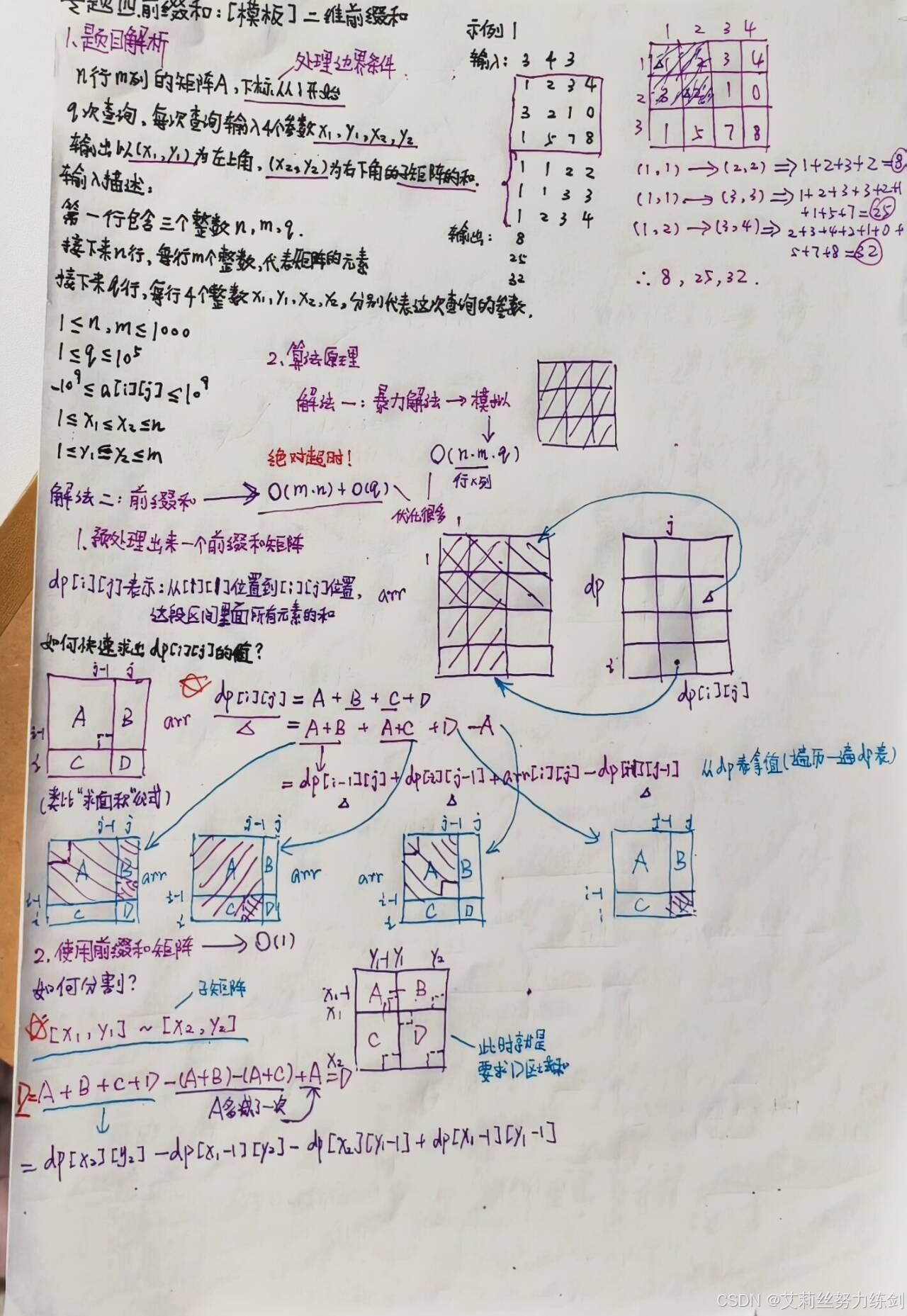
1、先预处理出来一个【前缀和】数组——用dp[ i ]表示。 [1 , i ]区间内所有元素的和，那么dp[i - 1]里面存的就是[1 , i - 1]区间内所有元素的和，那么——可得递推公式：dp[ i ] = dp[i－1] + arr[ i ]； 2、使用前缀和数组，【快速】求出【某一个区间内】所有元素的和：当询问的区间是[ l , r ]时：区间内所有元素的和为：dp[ r ] - dp[l - 1]。

1.2 算法实现

1.2.1 C++实现

代码演示如下——

#include <iostream>
#include<vector> // 创建数组
using namespace std;


int main()
{
    // 1、读入数据
    int n,m;
    cin >> n >> m;
    vector<int> arr(n + 1); // 刚开始默认0
    for(int i = 1;i <= n;i++) cin >> arr[i];

    // 2、预处理出来一个前缀和数组
    vector<long long> dp(n + 1); // 有可能栈溢出，防止溢出
    for(int i = 1;i <= n;i++) dp[i] = dp[i - 1] + arr[i];

    // 3、使用前缀和数组
    int l = 0,r = 0;
    while(m--)
    {
        cin >> l >> r;
        cout<< dp[r] - dp[l - 1] <<endl;
    }

    return 0;
}

时间复杂度：O(1)，空间复杂度：O(1)。

1.2.2 Java实现

代码演示如下——

import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息 
public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int q = scan.nextInt();
        // 为了防⽌溢出，⽤ long 类型的数组 
        int[] arr = new int[n + 1];
        long[] dp = new long[n + 1];
        for (int i = 1; i <= n; i++) { // 读数据 
            arr[i] = scan.nextInt();
        }
        for (int i = 1; i <= n; i++) { // 处理前缀和数组 
            dp[i] = dp[i - 1] + arr[i];
        }
        while (q > 0) {
            int l = scan.nextInt();
            int r = scan.nextInt();
            System.out.println(dp[r] - dp[l - 1]); // 使⽤前缀和数组 
            q--;
        }
    }
}

时间复杂度：O(1)，空间复杂度：O(1)。

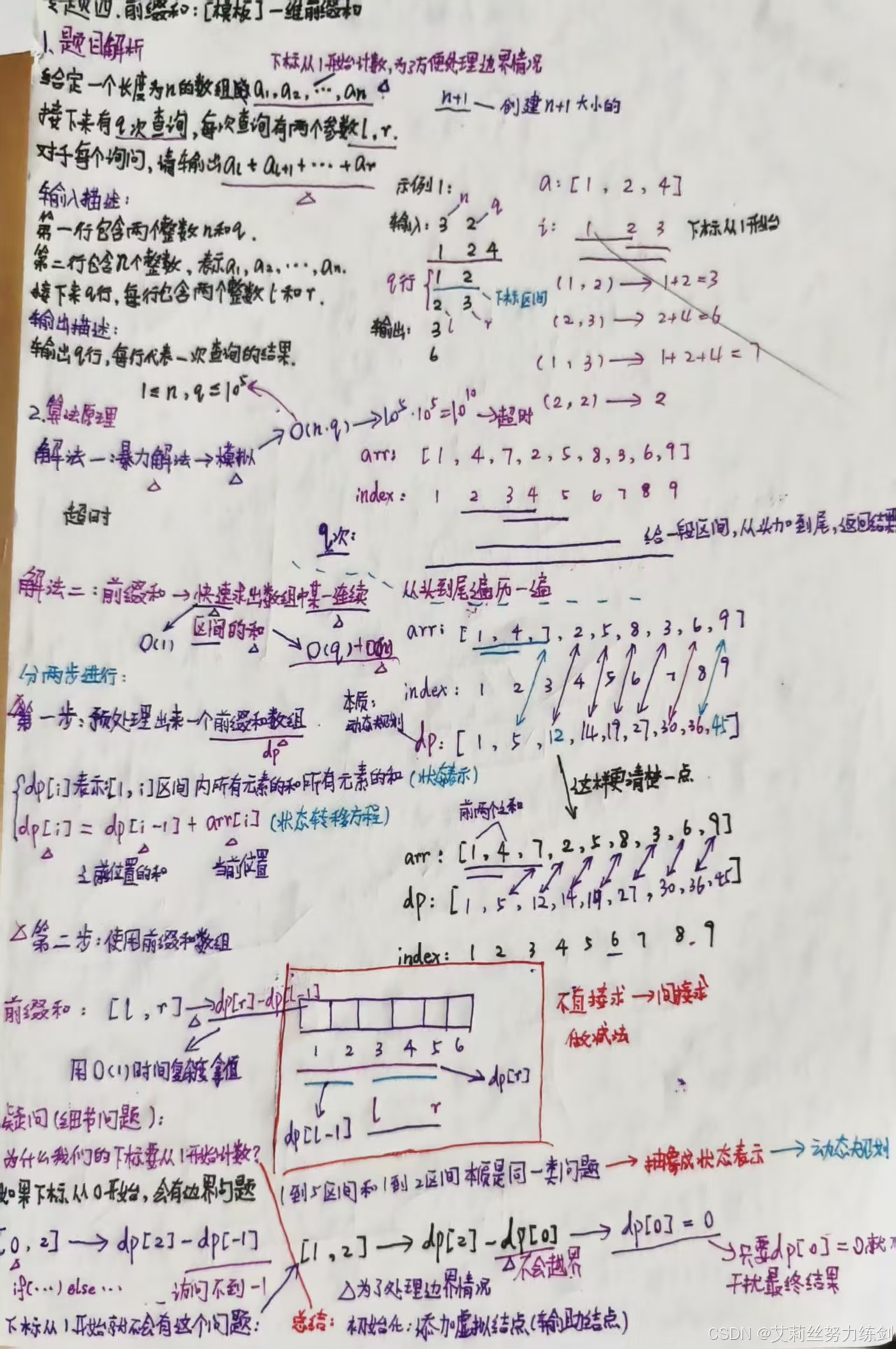
1.3 博主手记

本题整个的思路、算法原理、解题过程博主在纸上推导了一遍，大家可以参考一下手记的推导过程！最好做题的过程中自己也推导一遍！！！自己能够推导很重要！

026 【模板】二维前缀和

牛客网链接：DP35 【模板】二维前缀和

题目描述：

2.1 算法思路：前缀和

类比于一维数组的形式，如果我们能处理出来从[0 , 1]位置到[i , j]位置这片区域内所有元素的累加和，就可以在O(1)的时间内，搞定矩阵内任意区域内所有元素的累加和。因此我们接下来仅需完成两步即可——

2.1.1 第一步：搞出来前缀和矩阵

这里就要用到一维数组里面的拓展知识，我们要在矩阵的最上面和最左边添加上一行和一列0，这样我们就可以省去非常多的边界条件的处理（uu们可以自行尝试直接搞出来前缀和矩阵，边界条件的处理会让你崩溃的）。处理后的矩阵就像这样——

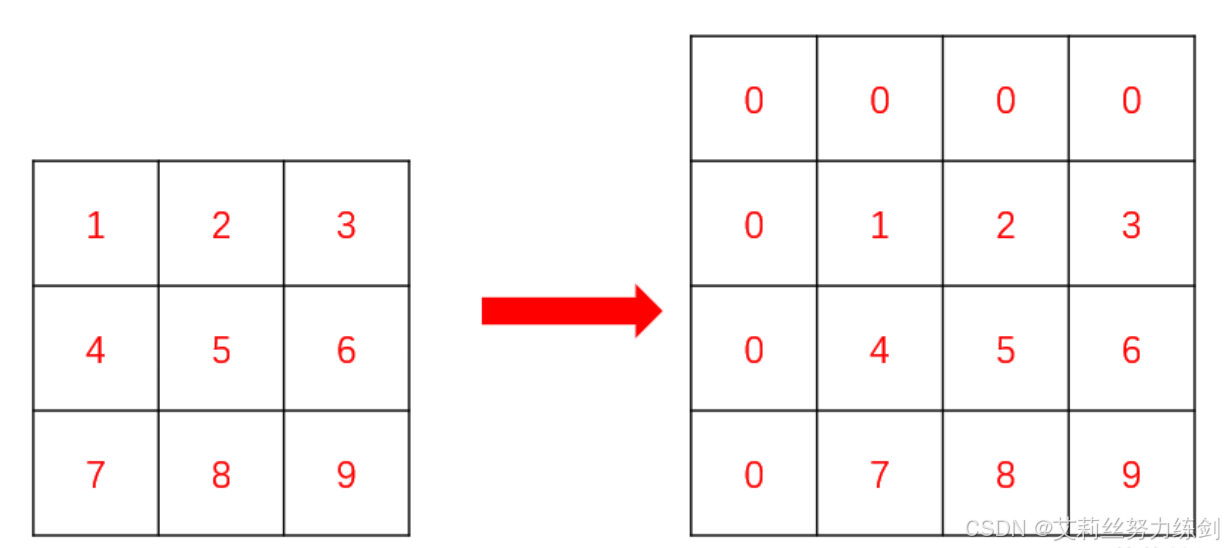
这样，我们填写前缀和矩阵数组的时候，下标直接从开始，能大胆使用i－1，j－1位置的值。

注意dp表与原数组matrix内的元素的映射关系：（1）从dp表到利matrix矩阵，横纵坐标减一；（2）从matrix矩阵到dp表，横纵坐标加一。

2.1.2 前缀和矩阵中sum[ i ][ j ]的含义，以及如何递推二维前缀和方程

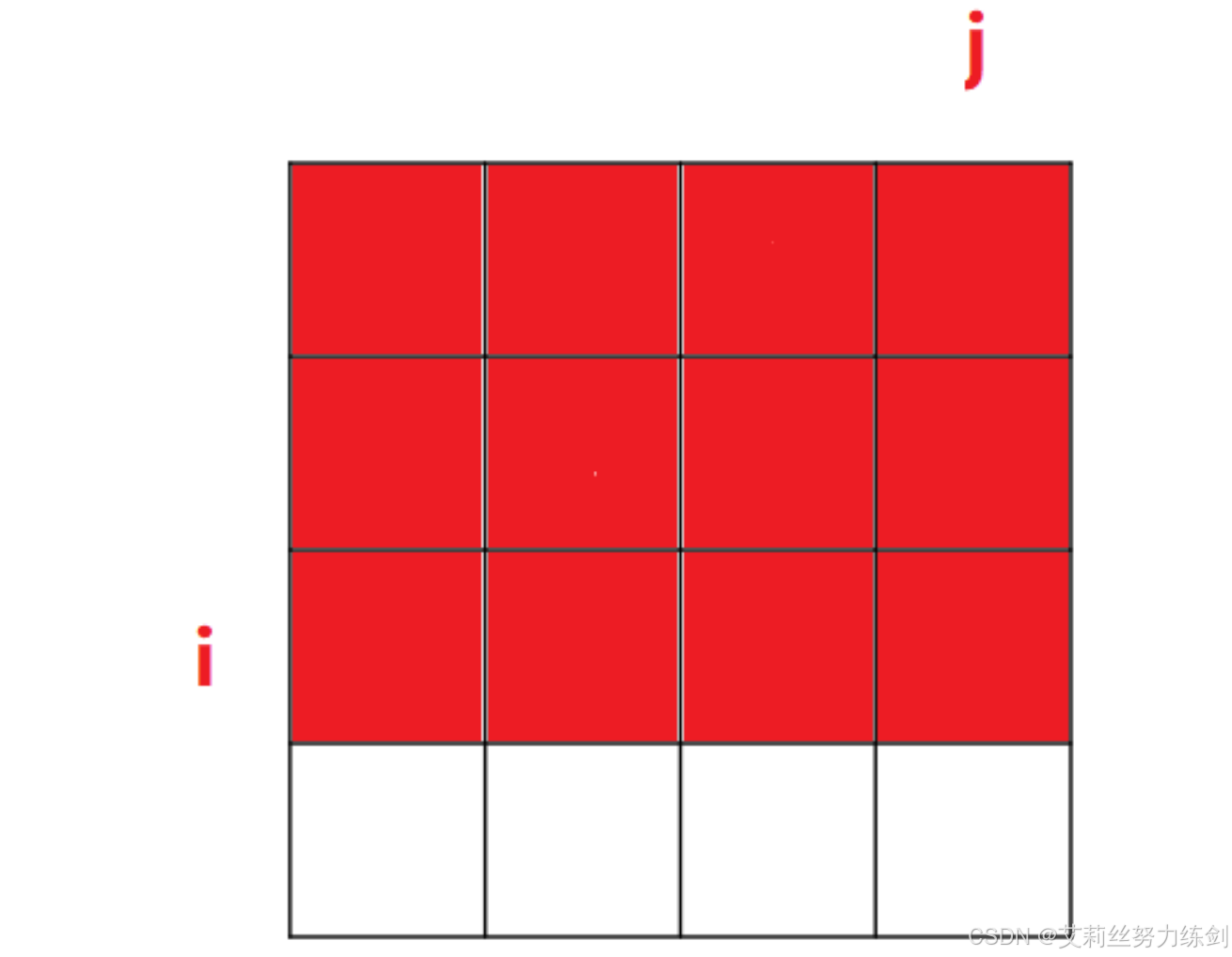
1、sum[ i ][ j ]的含义——

sum[ i ][ j ]表示，从[0 , 0]

位置到[i , j]位置这段区域内，所有元素的累加和。对应下图的红色区域：

2、递推方程——

其实这个递推方程非常像我们小学做过求图形面积的题，我们可以将[0 , 0]位置到[i , j]位置这段区域分解成下面的部分：

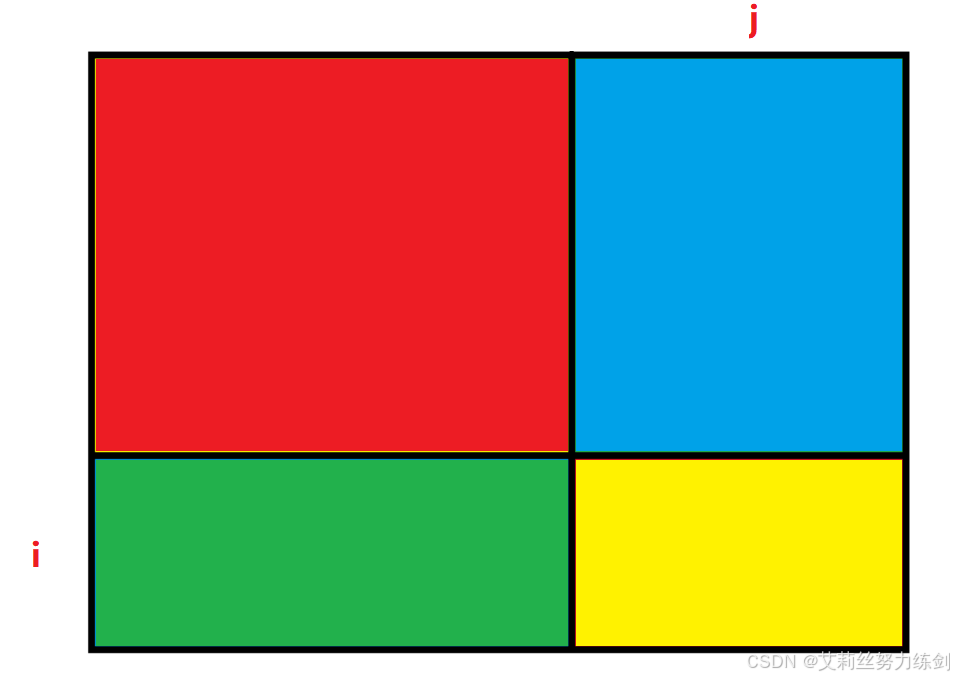
sum[ i ][ j ] = 红 + 蓝 + 绿 + 黄，分析一下这四块区域——

（1）黄色部分最简单，它就是数组中的matrix[i - 1][j - 1]（注意坐标的映射关系）；（2）单独的蓝不好求，因为它不是我们定义的状态表示中的区域，同理，单独的绿也是；（3）但是如果是红+蓝，正好是我们dp数组中sum[i－1][ j ]的值，美滋滋；（4）同理，如果是红+绿，正好是我们dp数组中sum[ i ][j - 1]的值；（5）如果把上面求的三个值加起来，那就是黄 + 红 + 蓝 + 红 + 绿，发现多算了一部分红的面积，因此再单独减去红的面积即可；（6）红的面积正好也是符合dp数组的定义的，即sum[i－1][j－1]。

综上所述，我们的递推方程就是——

sum[ i ][ j ] = sum[i - 1][ j ] + sum[ i ][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1]

2.1.3 第二步：使用前缀和矩阵

题目的接口中提供的参数是原始矩阵的下标，为了避免下标映射错误，这里直接先把下标映射成dp表里面对应的下标——

rowl++，col1++，row2++，col2++

接下来分析如何使用这个前缀和矩阵，如下图（注意这里的row和col都处理过了，对应的正是sum矩阵中的下标）：

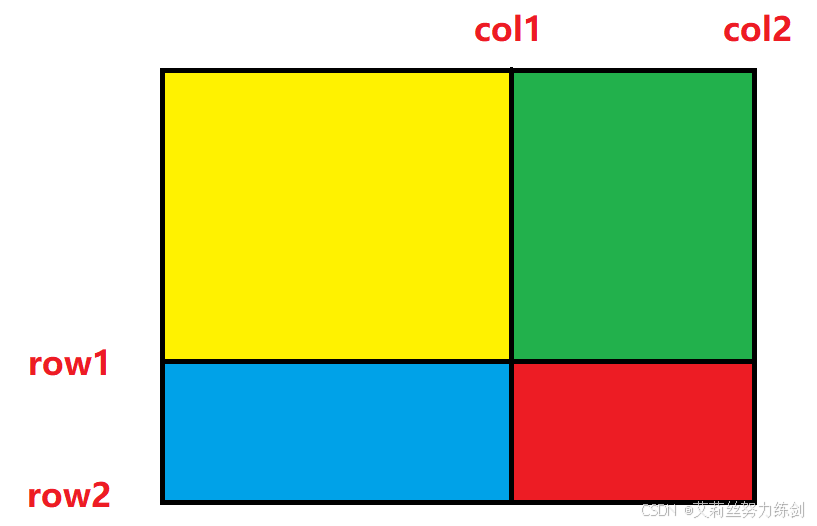
对于左上角（row1，col1）、右下角（row2，col2)围成的区域，正好是红色的部分。因此我们要求的就是红色部分的面积，继续分析几个区域：

（1）黄色，能直接求出来，就是sum[row1－1，col1－1](为什么减1，因为要剔除掉row这一行和col这一列）；（2）绿色，直接求不好求，但是和黄色拼起来，正好是sum表内sum[rowl - 1][col2]的数据；（3）同理，蓝色不好求，但是蓝 + 黄 = sum[row2][col1－1]；（4）再看看整个面积，好求嘛？非常好求，正好是sum[row2][col2]；（5）那么，红色就=整个面积-黄-绿-蓝，但是绿蓝不好求，我们可以这样减：整个面积 - (绿 + 黄) - (蓝 + 黄），这样相当于多减去了一个黄，再加上即可。

综上所述：红 = 整个面积 - (绿 + 黄) - (蓝 + 黄) + 黄，从而可得红色区域内的元素总和为——

sum[row2][col2] - sum[row2][col1 - 1] - sum[row1 - 1][col2] + sum[rowl - 1][col1 - 1]

2.2 算法实现

2.2.1 C++实现

#include <iostream>
#include<vector>
using namespace std;

int main()
{
    // 1.读入数据
    int n = 0,m = 0,q = 0;
    cin >> n >> m >> q;
    vector<vector<int>> arr(n + 1,vector<int>(m + 1));
    for(int i = 1;i <= n;++i) 
        for(int j = 1;j <= m;j++)
            cin >> arr[i][j];

    // 2.预处理前缀和矩阵
    vector<vector<long long>> dp(n + 1,vector<long long>(m + 1)); // 防止栈溢出
    for(int i = 1;i <= n;i++) 
        for(int j = 1;j <= m;j++)
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];

    // 3.使用前缀和矩阵
    int x1 = 0,y1 = 0,x2 = 0,y2 = 0;
    while(q--)
    {
            cin >> x1 >> y1 >> x2 >> y2;
            cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl;
    }

    return 0;
}

时间复杂度：O(1)，空间复杂度：O(1)。

2.2.2 Java实现

import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息 
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int q = in.nextInt();
        int[][] arr = new int[n + 1][m + 1];
        long[][] dp = new long[n + 1][m + 1];
        // 读入数据 
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                arr[i][j] = in.nextInt();

        // 处理前缀和矩阵 
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] +
                arr[i][j];

        // 使用前缀和矩阵 
        while (q > 0)
        {
            int x1 = in.nextInt(), y1 = in.nextInt(), x2 = in.nextInt(), y2 =
                in.nextInt();
            System.out.println(dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] +
                dp[x1 - 1][y1 - 1]);
            q--;
        }
    }
}

时间复杂度：O(1)，空间复杂度：O(1)。

2.3 博主手记

结尾

往期回顾：

【优选算法必刷100题】第023~24题（二分查找算法）：寻找/搜索旋转排序数组中的最小值、点名（缺失的数字）

结语：都看到这里啦！请大佬不要忘记给博主来个“一键四连”哦！

🗡博主在这里放了一只小狗，大家看完了摸摸小狗放松一下吧！🗡 ૮₍ ˶ ˊ ᴥ ˋ˶₎ა

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-10-23，如有侵权请联系 cloudcommunity@tencent.com 删除

数据

数组

算法

int

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体同步曝光计划，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度