【算法学习】位运算篇：位运算相关算法详解

一、常见位运算总结

在讲解例题前，我们先来看一下位运算一般会出现在什么场景中，以及如何使用，需要注意的是本篇学习的前提是你要掌握基本的位运算的知识点，比如运算符及二进制等

1.1 基础位运算

• 按位与 &:有0就是0
• 按位或|:有1就是1
• 按位异或^:相同为0，相异为1（其实就是无进位相加）

1.2 确定一个数的二进制表示中第x位是0还是1

• 比如数n:0110101001
• 我们要判断它的第x位是0还是1
• 我们只需要让它左移x位然后按位与1

1.3 将一个数二进制表示中的第x位修改成1

• 比如数n:0110101001
• 我们要让第x位修改位1
• 我们只需要让1左移x位然后与它按位或

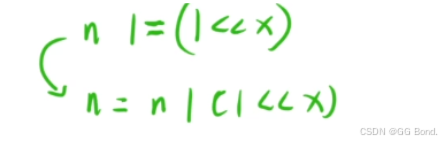
1.4 将一个数二进制表示中的第x位修改成0

• 比如数n:0110101001
• 我们要让第x位修改为0
• 我们只需要让1左移x位，然后再取反，然后与它按位与

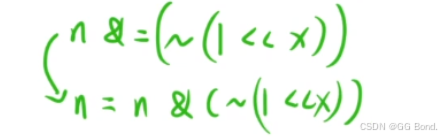
1.5 位图的思想

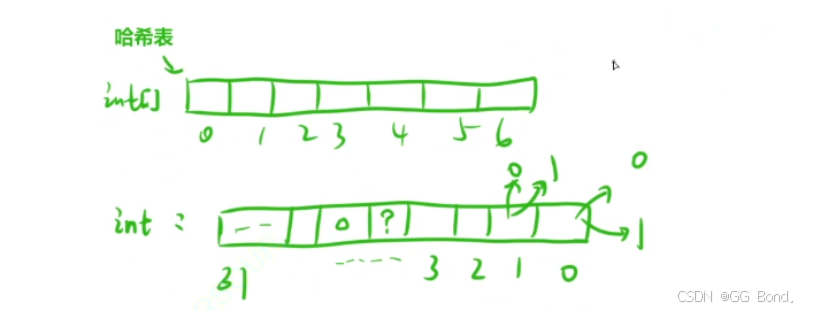
解释:位图有一点像哈希表，但与哈希表不同的是，哈希表是通过一个数组中不同位置不同的数来表示这个位置的状态，而位图则是通过一个整数中比特位的取值来表示这个位置的状态

1.6 提取一个数二进制表示中最右侧的1

采用方法:n&(-n)

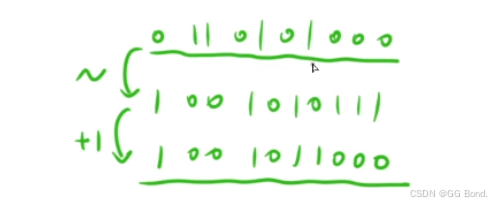
解释:一个数的负数，就是在原数的基础上取反再加1

比如上面这个例子，我们仔细观察其实就可以得到-n的本质就是 : 将n最右侧的1的左边的位置全部取反(包含最右侧1)

1.7 干掉一个数二进制表示中最右侧的1

采用方法:n&(n-1)

解释:观察这个例子我们就可以看出来 n-1操作的本质就是:将n最右侧1的右边位置全部取反(包含最右侧1)

1.8 位运算的优先级

能加括号就加括号

1.9 异或（^）运算的运算律

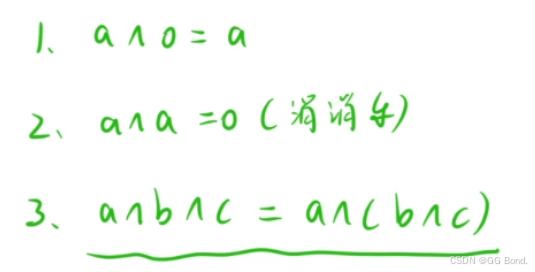
二、经典例题

下面所涉及的例题都是leetcode上的，建议看完之后可以自己去写一下

2.1 判定字符是否唯一

面试题 01.01. 判定字符是否唯一

实现一个算法，确定一个字符串 s 的所有字符是否全都不同。

示例 1：

输入: s= "leetcode"输出: false 

示例 2：

输入: s= "abc"输出: true

限制：

• 0 <= len(s) <= 100
• s[i]仅包含小写字母
• 如果你不使用额外的数据结构，会很加分。

解法一: 哈希表(比较简单，这里就不讲了)

解法二：位图

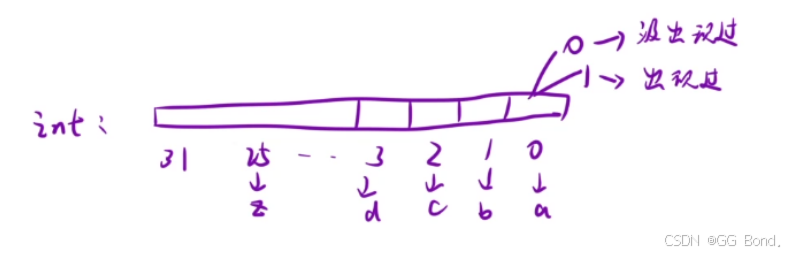
解释:我们可以采用位图的思想，位图的不同比特位的位置代表一个字符，所以可以用一个32位整形的前26位表示一个字符，0代表没出现过，1代表出现过 同时我们还可以用鸽巢原理做一下优化，因为只有26个字符，所以当单词中字符个数大于26时一定会有重复

实现代码：

class Solution {
public:
    bool isUnique(string astr) {
        if(astr.size()>26) return false;
        int bitMap=0;
        for(auto e:astr)
        {
            int i=e-'a';
            if((bitMap>>i)&1) return false;
            else bitMap|=(1<<i);
        }
        return true;
    }
};

2.2 两整数之和

371. 两整数之和

给你两个整数 a 和 b ，不使用 运算符 + 和 - ，计算并返回两整数之和。

示例 1：

输入：a = 1, b = 2
输出：3

示例 2：

输入：a = 2, b = 3
输出：5

提示：

• -1000 <= a, b <= 1000

解法:位运算(异或运算-无进位相加)

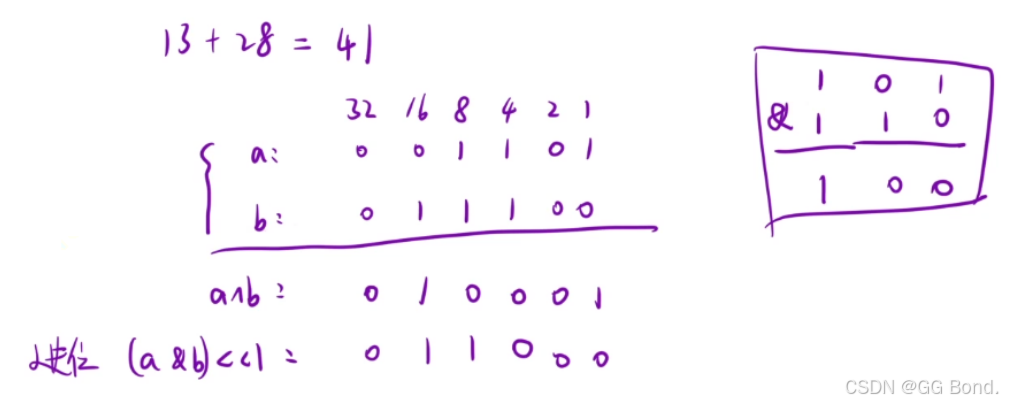
解释:在上面我们提过异或运算其实就是一个无进位相加，所以我们只需要找到需要进位的位置，并将这个位置进位后再与异或后的值相加即可，相加的时候就需要重复上述操作直到没有可以进位的位置 这里我们可以注意到的就是:其实需要进位的位置就是两个1的时候，而同为1时我们按位与就能找到它，但是找到的是原位置的，所以我们需要让它<<1左移1位

代码实现：

class Solution {
public:
    int getSum(int a, int b) {
        while(b!=0)
        {
            int tmp1=a,tmp2=b;
            a=tmp1^tmp2;
            b=(tmp1&tmp2)<<1;
        }
        return a;
    }
};

2.3 只出现一次的数字||

137. 只出现一次的数字 II

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

示例 1：

输入：nums = [2,2,3,2]
输出：3

示例 2：

输入：nums = [0,1,0,1,0,1,99]
输出：99

提示：

• 1 <= nums.length <= 3 * 104
• -231 <= nums[i] <= 231 - 1
• nums 中，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次

解释:如图，一个整数有32个比特位，除了一个元素出现一次外，其它元素均出现3次，所以将所有数字相加，它们在任意一个比特位上的和按理说都是3n的倍数或倍数加1，这取决于这个单独的数

代码实现：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret=0;
        for(int i=0;i<32;i++)
        {
            int sum=0;
            for(auto e:nums)
            {
                if((e>>i)&1==1) sum++;
            }
            sum%=3;
            ret|=(sum<<i);
        }
        return ret;
    }
};

2.4 消失的两个数字

面试题 17.19. 消失的两个数字

给定一个数组，包含从 1 到 N 所有的整数，但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗？

以任意顺序返回这两个数字均可。

示例 1：

输入：[1]
输出：[2,3]

示例 2：

输入：[2,3]
输出：[1,4]

提示：

• nums.length <= 30000

本题与上面例题中的260思路基本一致，可以结合例题中的题解学习一下 //1.将所有数异或到一起 // 2.找到 a，b中比特位不同的那一位 //3.根据diff位的不同，将所有的数划为两类来异或

代码实现：

class Solution {
public:
    vector<int> missingTwo(vector<int>& nums) {
        // 1.将所有数异或到一起
        int tmp = 0;
        for (auto x : nums)
            tmp ^= x;
        for (int i = 1; i <= nums.size() + 2; i++)
            tmp ^= i;
        // 2.找到 a，b中比特位不同的那一位
        int diff = 0;
        while (1) {
            if ((tmp >> diff) & 1 == 1)
                break;
            else
                diff++;
        }
        // 3.根据diff位的不同，将所有的数划为两类来异或
        int a = 0, b = 0;
        for (int x : nums)
            if ((x >> diff) & 1 == 1)
                b ^= x;
            else
                a ^= x;
        for (int i = 1; i <= nums.size() + 2; i++)
            if ((i >> diff) & 1 == 1)
                b ^= i;
            else
                a ^= i;
        return {a, b};
    }
};

三、总结

总之，位运算在处理数字上会经常用到，尤其是当涉及这种二进制的相关操作时，我们要结合位运算的基本操作，多去思考数字二进制表示后的形态，可以在纸上写写找规律

本篇笔记：

感谢各位大佬观看，创作不易，还望各位大佬点赞支持！！！