随机变量的数学期望

简介

基本概念

数学期望（或均值，亦简称期望）是概率论和统计学中的一个基本概念，它反映了随机变量在多次试验中平均取值的大小。具体来说，数学期望是试验中每次可能结果的概率乘以其结果的总和。

数学期望的定义

1、对于离散型随机变量，其数学期望 𝐸(𝑋)E(X) 定义为： 𝐸(𝑋)=∑𝑖=1𝑛𝑝𝑖𝑥𝑖E(X)=∑i=1n​pi​xi​ 其中 𝑥𝑖xi​ 为随机变量 𝑋X 的可能值，𝑝𝑖pi​ 为其对应的概率。 2、对于连续型随机变量，其数学期望 𝐸(𝑋)E(X) 定义为： 𝐸(𝑋)=∫−∞∞𝑥𝑓(𝑥)𝑑𝑥E(X)=∫−∞∞​xf(x)dx 其中 𝑓(𝑥)f(x) 为随机变量 𝑋X 的概率密度函数。

数学期望的性质

数学期望具有以下重要性质：

1. 线性性：如果 𝑎a 和 𝑏b 是常数，则有： 𝐸(𝑎𝑋+𝑏𝑌+𝑐)=𝑎𝐸(𝑋)+𝑏𝐸(𝑌)+𝑐E(aX+bY+c)=aE(X)+bE(Y)+c 这表明数学期望具有线性关系。
2. 独立性：如果两个随机变量 𝑋X 和 𝑌Y 是相互独立的，则有： 𝐸(𝑋𝑌)=𝐸(𝑋)𝐸(𝑌)E(XY)=E(X)E(Y) 这一性质在处理复杂问题时非常有用。
3. 不变性：如果 𝑐c 是常数，则有： 𝐸(𝑐)=𝑐E(c)=c 这说明常数的期望值就是该常数本身。

数学期望的应用

数学期望在实际应用中有着广泛的应用，例如在工程、金融、医疗等领域。它不仅用于评估随机变量的平均取值，还用于计算方差、协方差等其他数字特征。此外，数学期望的概念也扩展到了条件期望、矩以及相关系数等更复杂的统计量中。

计算实例

假设我们玩一个游戏，有52张牌，其中有4个A。我们可以计算抽到一张A的概率及其期望值。设 𝑋X 表示抽到A的次数，则：𝑃(𝑋=1)=452,𝑃(𝑋=0)=4852P(X=1)=524​,P(X=0)=5248​ 因此，数学期望 𝐸(𝑋)E(X) 可以通过以下公式计算： 𝐸(𝑋)=1×452+0×4852=113≈0.0769 E(X)=1×524​+0×5248​=131​≈0.0769 通过这些例子和性质，我们可以更好地理解和运用数学期望这一重要的统计工具。

数学期望在解决哪些具体问题时最为有效？

数学期望在解决许多具体问题时非常有效，这些领域包括但不限于医疗、经济、数据分析、社会活动以及彩票抽奖等。以下是一些具体的例子和应用：

1. 医疗领域：在疾病普查中，通过计算平均值来预测疾病的分布情况，从而制定更有效的公共卫生策略。
2. 经济领域：在商业决策中，如进货量对利润的影响分析，利用数学期望可以预测不同进货量下的预期收益，帮助企业在风险管理和利润最大化方面做出更明智的决策。
3. 体育赛事：赛制设计中的胜负预测，通过计算各参赛队伍的平均得分或胜率，可以评估不同赛制对比赛结果的影响。
4. 保险业：保险公司利用数学期望来评估风险和定价保险产品，例如通过计算索赔金额的期望值来确定保费。
5. 投资决策：在金融投资中，投资者可以通过计算投资项目的期望回报率来评估其潜在收益和风险，从而做出更加理性的投资选择。
6. 彩票：虽然看似随机，但通过计算各种可能结果的期望值，可以帮助人们理解购买彩票的长期期望收益，从而避免过度投资。
7. 决策支持：在各种实际问题中，如求职决策、进货量等，数学期望可以帮助决策者评估不同选项的平均效果，从而做出最优选择。

数学期望作为一种重要的数字特征，在多个领域的实际问题解决中都显示出了其强大的应用价值和有效性。

如何计算两个或多个随机变量的组合概率及其期望值？

计算两个或多个随机变量的组合概率及其期望值，需要综合运用概率论和统计学中的多种方法。以下是详细的步骤和公式：

1. 计算组合概率

对于两个独立随机变量 𝑋X 和 𝑌Y，其联合概率密度函数 𝑓𝑋,𝑌(𝑥,𝑦)fX,Y​(x,y) 可以表示为： 𝑓𝑋,𝑌(𝑥,𝑦)=𝑓𝑋(𝑥)⋅𝑓𝑌(𝑦)fX,Y​(x,y)=fX​(x)⋅fY​(y) 其中，𝑓𝑋(𝑥)fX​(x) 和 𝑓𝑌(𝑦)fY​(y) 分别是 𝑋X 和 𝑌Y 的概率密度函数。 如果要计算这两个随机变量的某个特定事件的概率，比如 𝑋+𝑌≤𝑐X+Y≤c，则可以通过积分来求解： 𝑃(𝑋+𝑌≤𝑐)=∫−∞∞∫−∞𝑐−𝑦𝑓𝑋,𝑌(𝑥,𝑦) 𝑑𝑥 𝑑𝑦P(X+Y≤c)=∫−∞∞​∫−∞c−y​fX,Y​(x,y)dxdy

2. 计算期望值

期望值的计算公式为： 𝐸[𝑋]=∑𝑥𝑥⋅𝑃(𝑋=𝑥)E[X]=∑x​x⋅P(X=x) 对于连续随机变量，期望值的计算公式为： 𝐸[𝑋]=∫−∞∞𝑥⋅𝑓𝑋(𝑥) 𝑑𝑥E[X]=∫−∞∞​x⋅fX​(x)dx 其中，𝑃(𝑋=𝑥)P(X=x) 和 𝑓𝑋(𝑥)fX​(x) 分别是离散和连续随机变量的概率分布函数。

当涉及到两个或多个随机变量的组合时，可以使用以下几种方法：

线性组合的期望值 对于两个独立随机变量 𝑋X 和 𝑌Y 的线性组合 𝑍=𝑎𝑋+𝑏𝑌+𝑐Z=aX+bY+c，其期望值 𝐸[𝑍]E[Z] 可以通过以下公式计算： 𝐸[𝑍]=𝑎𝐸[𝑋]+𝑏𝐸[𝑌]+𝑐E[Z]=aE[X]+bE[Y]+c 这个性质说明了期望值在进行线性变换时的可加性。 联合高斯分布 如果两个随机变量 𝑋X 和 𝑌Y 都服从高斯分布，并且它们是独立的，则它们的联合分布也是高斯分布。在这种情况下，两个变量的联合均值和协方差可以用来计算它们的联合概率密度函数。此外，它们的线性组合仍然服从高斯分布。

3. 具体例子

假设 𝑋X 和 𝑌Y 是两个独立的正态分布随机变量，其均值分别为 𝜇𝑋μX​ 和 𝜇𝑌μY​，标准差分别为 𝜎𝑋σX​ 和 𝜎𝑌σY​。我们希望计算 𝑍=𝑋+𝑌Z=X+Y 的期望值和方差。

• 期望值： 𝐸[𝑍]=𝐸[𝑋+𝑌]=𝐸[𝑋]+𝐸[𝑌]=𝜇𝑋+𝜇𝑌E[Z]=E[X+Y]=E[X]+E[Y]=μX​+μY​
• 方差： Var(𝑍)=Var(𝑋+𝑌)=Var(𝑋)+Var(𝑌)=𝜎𝑋2+𝜎𝑌2Var(Z)=Var(X+Y)=Var(X)+Var(Y)=σX2​+σY2​

条件期望的概念是什么，它在统计分析中如何应用？

条件期望（Conditional Expectation）是概率论和统计学中的一个重要概念，它指的是在给定某些信息的情况下，对随机变量的期望值。具体来说，如果有一个随机变量 𝑋X 和另一个随机变量 𝑌Y，那么在已知 𝑌=𝑦Y=y 的条件下，𝑋X 的条件期望记作 𝐸[𝑋∣𝑌=𝑦]E[X∣Y=y]，表示在 𝑌Y 取特定值时，𝑋X 的平均取值。

条件期望的定义与性质

条件期望可以看作是在给定 𝑌=𝑦Y=y 的条件下，𝑋X 的概率加权平均值。其数学表达式为：

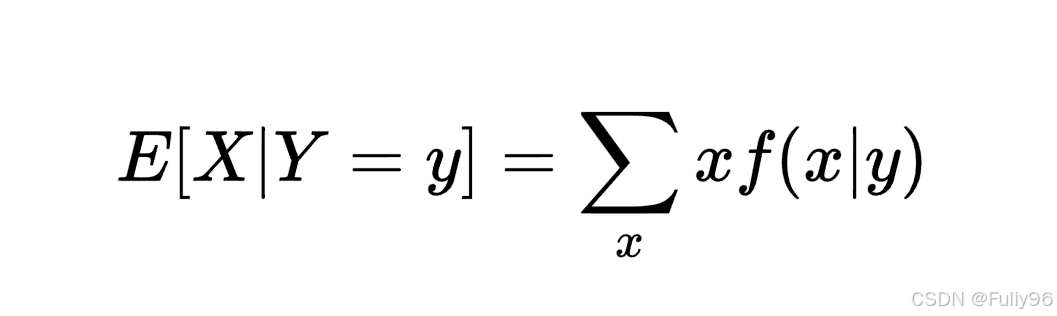
其中，𝑓(𝑥∣𝑦)f(x∣y) 是在 𝑌=𝑦Y=y 条件下 𝑋X 的概率密度函数或概率质量函数。

1. 性质：
   • 线性性：条件期望是一个线性算子，即对于任意常数 𝑎a 和 𝑏b，有：

   

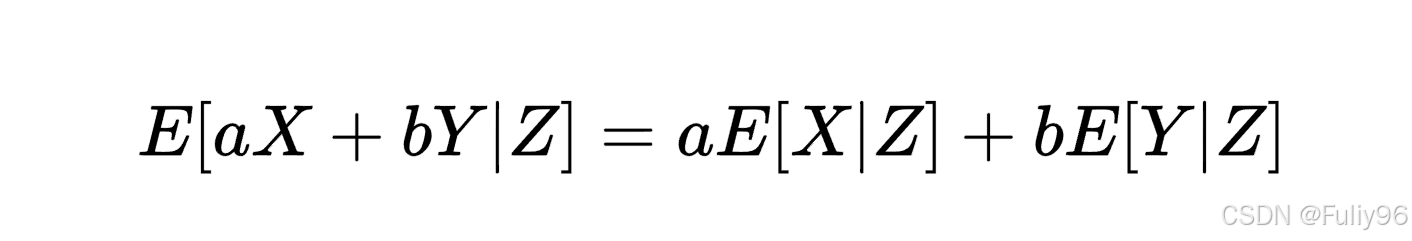
   • 无条件期望与条件期望的关系：如果 𝑋X 和 𝑌Y 独立，则 𝐸[𝑋𝑌]=𝐸[𝑋]𝐸[𝑌]E[XY]=E[X]E[Y]，否则需要考虑它们的联合分布。

条件期望在统计分析中的应用

在线性回归模型中，条件期望用于预测因变量的值。例如，在给定自变量 𝑋1,𝑋2,…,𝑋𝑛X1​,X2​,…,Xn​ 的情况下，预测因变量 𝑌Y 的值。这可以通过最小二乘法来实现，假设条件期望与自变量呈线性关系，并使用样本估计参数如 𝛽1β1​ 和 𝛽2β2​ 来拟合模型。 条件期望还可以用于预测和评估预测模型的效果。通过计算预测值与实际值之间的差异，可以评估模型的准确性。例如，在时间序列分析中，利用过去的观测数据来预测未来的值，并通过计算预测误差来判断模型的性能。 在计量经济学中，条件期望常用于分析因果关系及其他条件不变的分析方法。通过构建合适的数学模型，可以利用历史数据来预测未来的变化趋势。 条件期望在许多其他统计方法中也有广泛应用，如假设检验、置信区间估计以及各种概率分布的参数估计等。这些方法通常依赖于条件期望的性质和计算公式来进行推断和分析。 总之，条件期望不仅是理解随机变量之间关系的基础工具，也是现代统计分析中不可或缺的一部分。

矩的概念及其与数学期望的关系是什么？

矩（moment）是描述随机变量分布特征的一组数字特征，它在数学和统计学中具有重要地位。矩的概念最早源于物理学，用于表示物体形状的物理量，但在数学中，矩被用来度量一组具有一定形态特点的点阵。 具体来说，矩可以分为原点矩和中心矩两种类型。原点矩是指随机变量的某次幂的数学期望，例如一阶原点矩就是数学期望，即均值。二阶原点矩是方差，三阶原点矩是偏度，四阶原点矩是峰度等。中心矩则是从原点矩中减去其均值后的结果，例如二阶中心矩就是方差。 通过这些矩，我们可以更深入地了解随机变量的分布特性。例如，方差可以用来衡量数据的离散程度，而协方差则用于衡量两个随机变量之间的相关性。此外，高阶矩还可以帮助我们理解数据的形态特征，如偏度和峰度等。 总之，矩是一个非常广泛且强大的工具，能够提供关于随机变量分布的丰富信息。

相关系数是如何从数学期望的角度来计算的？

相关系数的计算可以从数学期望的角度来理解。具体来说，相关系数（通常用符号 𝜌ρ 表示）是通过协方差和标准差来计算的。其计算公式为： 𝜌𝑋,𝑌=Cov(𝑋,𝑌)Var(𝑋)⋅Var(𝑌)ρX,Y​=Var(X)⋅Var(Y)​Cov(X,Y)​ 其中，Cov(𝑋,𝑌)Cov(X,Y) 是变量 𝑋X 和 𝑌Y 的协方差，而 Var(𝑋)Var(X) 和 Var(𝑌)Var(Y) 分别是变量 𝑋X 和 𝑌Y 的方差。 协方差 Cov(𝑋,𝑌)Cov(X,Y) 可以通过以下公式计算： Cov(𝑋,𝑌)=𝐸[(𝑋−𝐸[𝑋])(𝑌−𝐸[𝑌])]Cov(X,Y)=E[(X−E[X])(Y−E[Y])] 其中，𝐸[𝑋]E[X] 和 𝐸[𝑌]E[Y] 分别是变量 𝑋X 和 𝑌Y 的数学期望。 标准差 Var(𝑋)Var(X) 和 Var(𝑌)Var(Y) 可以通过以下公式计算： Var(𝑋)=𝐸[(𝑋−𝐸[𝑋])2]Var(X)=E[(X−E[X])2] Var(𝑌)=𝐸[(𝑌−𝐸[𝑌])2]Var(Y)=E[(Y−E[Y])2]