低摆线动画matplotlib - python
低摆线动画matplotlib - python
提问于 2018-10-12 11:17:22
我试图从维基百科制作这个动画,然而,我很难弄清楚如何做到这一点。基本上,我需要做两件事:
- 将所有的图形绘制在一个框架中。
- 绘制最大圆并保持它,然后绘制最小圆和次摆线点。但是,我也需要保留下摆线的点,并更新最小圆的位置。
这是我的代码,但是我得到了十个不同的帧
import numpy as np
import matplotlib.pyplot as plt
R=3 #Biggest circle radius =3
r=1 #smallest circle radius =1
t=np.linspace(0, 2*np.pi,100) # values from zero to 360 degrees
i=0
xc1=R*np.cos(t) #biggest circle
yc1=R*np.sin(t) #biggest circle
plt.plot(xc1,yc1)
while i<=2*np.pi:
x=(R-r)*np.cos(i)+r*np.cos((R-r)*i/r) #x values of the hypocycloid
y=(R-r)*np.sin(i)-r*np.sin((R-r)*i/r)#y value of the hypocycloid
plt.plot(x,y)
i+=2*np.pi/10
plt.show()先谢谢你。
回答 1
Stack Overflow用户
发布于 2018-10-13 07:10:45
这里有一个完整的例子,使用OP链接到的维基百科页面中给出的方程。由于有相当多的变量需要跟踪,所以我认为最好在一个类中收集所有的内容。
from matplotlib import pyplot as plt
from matplotlib.animation import FuncAnimation
import numpy as np
class Hypocycloid:
def __init__(self, ratio = 3, frames = 100, ncycles = 1):
self.frames = frames
self.ncycles = ncycles
self.fig, self.ax = plt.subplots()
self.ax.set_aspect('equal')
##big circle:
theta = np.linspace(0,2*np.pi,100)
x = np.cos(theta)
y = np.sin(theta)
self.big_circle, = self.ax.plot(x,y,'b-')
##small circle:
self.small_r = 1./ratio
r = self.small_r
x = r*np.cos(theta)+1-r
y = r*np.sin(theta)
self.small_circle, = self.ax.plot(x,y,'k-')
##line and dot:
self.line, = self.ax.plot([1-r,1],[0,0],'k-')
self.dot, = self.ax.plot([1-r],[0], 'ko', ms=5)
##hypocycloid:
self.hypocycloid, = self.ax.plot([],[],'r-')
self.animation = FuncAnimation(
self.fig, self.animate,
frames=self.frames*self.ncycles,
interval=50, blit=False,
repeat_delay=2000,
)
def update_small_circle(self, phi):
theta = np.linspace(0,2*np.pi,100)
x = self.small_r*np.cos(theta)+(1-self.small_r)*np.cos(phi)
y = self.small_r*np.sin(theta)+(1-self.small_r)*np.sin(phi)
self.small_circle.set_data(x,y)
def update_hypocycloid(self, phis):
r = self.small_r
x = (1-r)*np.cos(phis)+r*np.cos((1-r)/r*phis)
y = (1-r)*np.sin(phis)-r*np.sin((1-r)/r*phis)
self.hypocycloid.set_data(x,y)
center = [(1-r)*np.cos(phis[-1]), (1-r)*np.sin(phis[-1])]
self.line.set_data([center[0],x[-1]],[center[1],y[-1]])
self.dot.set_data([center[0]], [center[1]])
def animate(self, frame):
frame = frame+1
phi = 2*np.pi*frame/self.frames
self.update_small_circle(phi)
self.update_hypocycloid(np.linspace(0,phi,frame))
hypo = Hypocycloid(ratio=3.25, frames = 40, ncycles=4)
##un-comment the next line, if you want to save the animation as gif:
##hypo.animation.save('hypocycloid.gif', writer='imagemagick', fps=10, dpi=75)
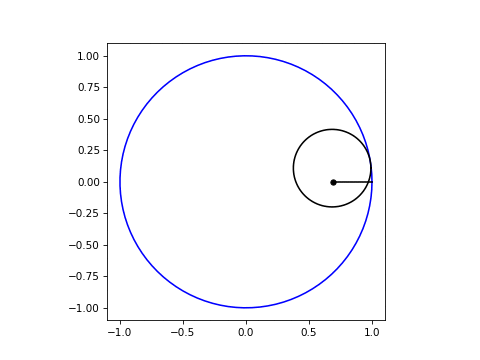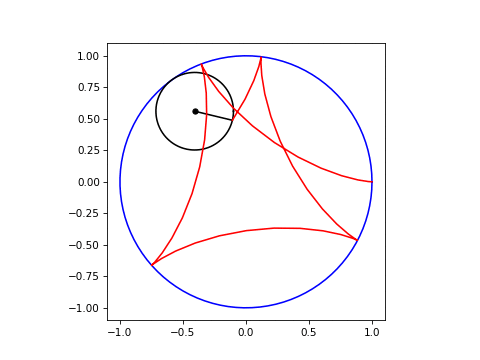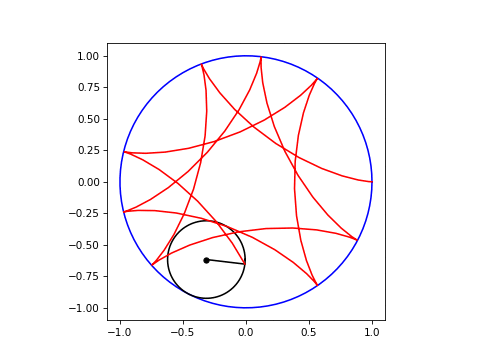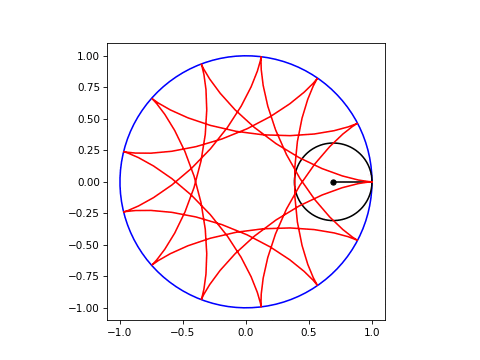
plt.show()可以传递给Hypocycloid类的参数是ratio (相对于大圆的小圆半径)、frames (围绕大圆的一次行程的帧数)和ncycles (trips数)。ratio=3.25、frames=40和ncycles=4的最终结果如下所示:
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/52785764
复制相似问题