《人工智能导论》第 6 章 智能计算及其应用
《人工智能导论》第 6 章 智能计算及其应用

啊阿狸不会拉杆
发布于 2026-01-21 12:24:15
发布于 2026-01-21 12:24:15
前言
智能计算作为人工智能领域的重要分支,通过模拟自然界的生物进化、群体智能等现象,为复杂问题求解提供了高效的计算范式。本章将系统介绍进化算法、遗传算法及其改进、粒子群优化算法和蚁群算法等核心内容,并通过 Python 代码实现帮助读者深入理解。
本章思维导图
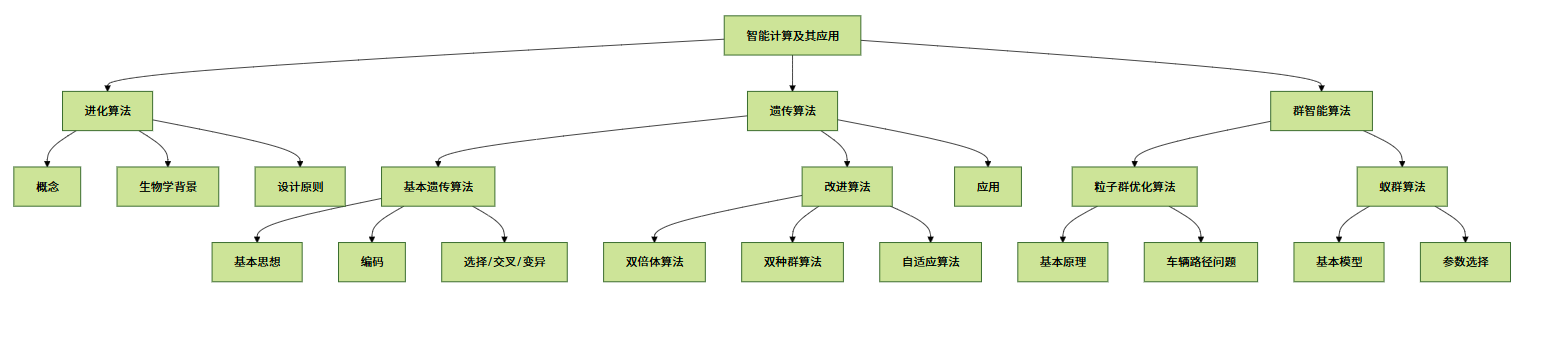
6.1 进化算法的产生与发展
6.1.1 进化算法的概念
进化算法 (Evolutionary Algorithms, EAs) 是一类模拟自然界生物进化过程与机制求解优化问题的自组织、自适应的随机搜索算法。它通过模拟自然选择和遗传过程中发生的繁殖、杂交、突变、竞争和选择等现象,来寻找最优解。
6.1.2 进化算法的生物学背景
- 自然选择:达尔文进化论的核心,适者生存,不适者淘汰
- 遗传变异:生物种群在繁殖过程中会发生基因重组和突变
- 种群进化:通过多代进化,种群对环境的适应度不断提高
6.1.3 进化算法的设计原则
- 适应性原则:设计合理的适应度函数衡量解的优劣
- 多样性原则:保持种群多样性避免早熟收敛
- 进化原则:通过选择、交叉、变异等操作推动种群进化
- 参数敏感性原则:合理设置种群规模、交叉变异概率等参数
6.2 基本遗传算法
6.2.1 遗传算法的基本思想
遗传算法 (Genetic Algorithm, GA) 通过模拟生物进化中的自然选择和遗传过程,将问题的解表示为 "染色体",通过选择、交叉、变异等操作迭代优化,最终找到最优解。
6.2.2 遗传算法的发展历史
- 1975 年,John Holland 出版《自然与人工系统的适应性》,奠定遗传算法基础
- 1989 年,David Goldberg 的《遗传算法在搜索、优化和机器学习中的应用》推动 GA 广泛应用
- 近年来,结合深度学习等领域形成新的研究方向
6.2.3 编码
遗传算法中常用的编码方式包括:
- 二进制编码:将参数编码为二进制串
- 实数编码:直接使用实数表示参数
- 符号编码:用于组合优化问题的编码
6.2.4 群体设定
- 种群规模:通常取 20-200,太大影响效率,太小影响多样性
- 初始化:随机生成初始种群,确保解空间覆盖
6.2.5 适应度函数
适应度函数是衡量个体优劣的标准,需根据具体问题设计。例如优化函数(f(x)=x^2),适应度函数可直接使用(f(x))。
遗传算法流程图
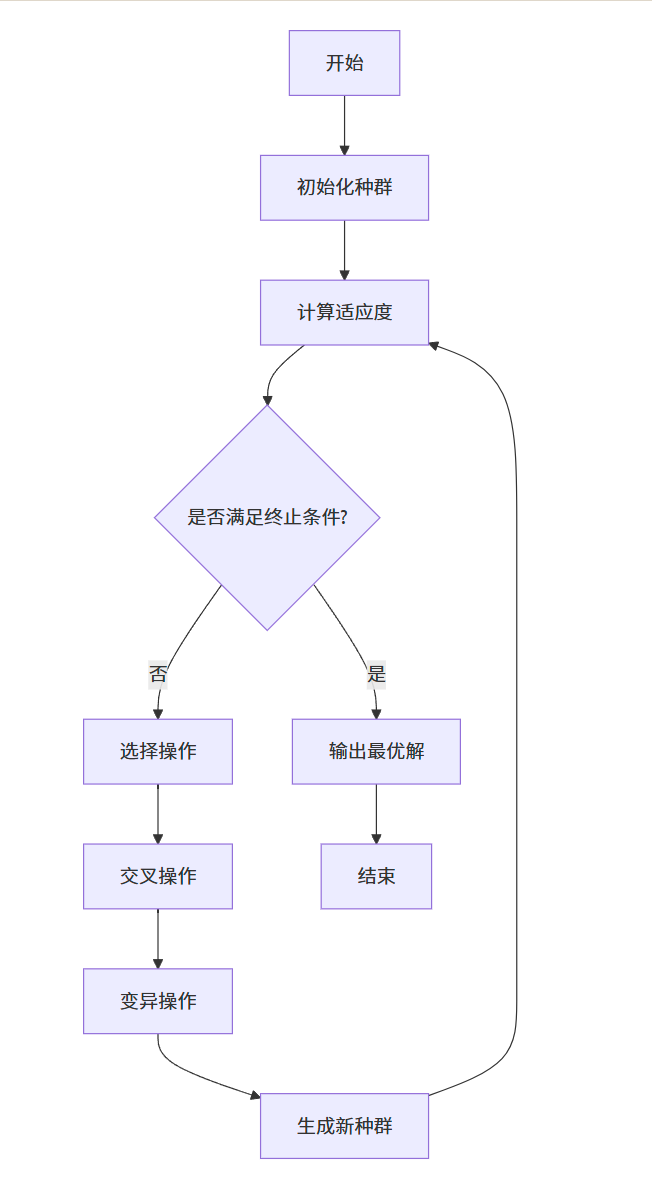
基本遗传算法 Python 实现案例
下面通过一个函数优化问题来实现基本遗传算法:寻找函数(f(x) = x^2)在区间 [-10, 10] 上的最大值。
import numpy as np
import matplotlib.pyplot as plt
from typing import List, Tuple, Callable
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class GeneticAlgorithm:
def __init__(
self,
population_size: int = 100,
chromosome_length: int = 22,
max_generations: int = 200,
crossover_prob: float = 0.8,
mutation_prob: float = 0.01,
x_range: Tuple[float, float] = (-10, 10)
):
"""
初始化遗传算法参数
参数:
population_size: 种群大小
chromosome_length: 染色体长度(二进制位数)
max_generations: 最大迭代次数
crossover_prob: 交叉概率
mutation_prob: 变异概率
x_range: 变量x的取值范围
"""
self.population_size = population_size
self.chromosome_length = chromosome_length
self.max_generations = max_generations
self.crossover_prob = crossover_prob
self.mutation_prob = mutation_prob
self.x_range = x_range
self.population = np.random.randint(0, 2, (population_size, chromosome_length))
self.best_fitness = 0
self.best_individual = None
self.best_x = 0
self.fitness_history = []
def decode_chromosome(self, chromosome: np.ndarray) -> float:
"""将二进制染色体解码为实数"""
decimal = 0
for i, gene in enumerate(chromosome):
decimal += gene * (2 ** (self.chromosome_length - 1 - i))
x = self.x_range[0] + decimal * (self.x_range[1] - self.x_range[0]) / (2 ** self.chromosome_length - 1)
return x
def fitness_function(self, x: float) -> float:
"""适应度函数: f(x) = x^2"""
return x ** 2
def calculate_fitness(self) -> np.ndarray:
"""计算种群中所有个体的适应度"""
fitness = np.zeros(self.population_size)
for i in range(self.population_size):
x = self.decode_chromosome(self.population[i])
fitness[i] = self.fitness_function(x)
# 记录最优个体
if fitness[i] > self.best_fitness:
self.best_fitness = fitness[i]
self.best_individual = self.population[i].copy()
self.best_x = x
self.fitness_history.append(np.mean(fitness))
return fitness
def selection(self, fitness: np.ndarray) -> np.ndarray:
"""轮盘赌选择操作"""
# 计算适应度总和
total_fitness = np.sum(fitness)
# 计算选择概率
selection_probs = fitness / total_fitness
# 计算累积概率
cumulative_probs = np.cumsum(selection_probs)
# 选择个体
new_population = np.zeros((self.population_size, self.chromosome_length), dtype=int)
for i in range(self.population_size):
r = np.random.random()
for j in range(self.population_size):
if r <= cumulative_probs[j]:
new_population[i] = self.population[j].copy()
break
return new_population
def crossover(self, population: np.ndarray) -> np.ndarray:
"""交叉操作"""
new_population = population.copy()
# 两两配对进行交叉
for i in range(0, self.population_size, 2):
if i + 1 < self.population_size and np.random.random() < self.crossover_prob:
# 随机选择交叉点
crossover_point = np.random.randint(1, self.chromosome_length)
# 交换交叉点后的基因
new_population[i, crossover_point:], new_population[i + 1, crossover_point:] = \
new_population[i + 1, crossover_point:].copy(), new_population[i, crossover_point:].copy()
return new_population
def mutation(self, population: np.ndarray) -> np.ndarray:
"""变异操作"""
for i in range(self.population_size):
for j in range(self.chromosome_length):
if np.random.random() < self.mutation_prob:
# 翻转基因(0变1, 1变0)
population[i, j] = 1 - population[i, j]
return population
def run(self) -> Tuple[float, float, List[float]]:
"""运行遗传算法"""
for generation in range(self.max_generations):
fitness = self.calculate_fitness()
population = self.selection(fitness)
population = self.crossover(population)
population = self.mutation(population)
self.population = population
if generation % 10 == 0:
print(f"Generation {generation}, Best fitness: {self.best_fitness}, Best x: {self.best_x}")
return self.best_fitness, self.best_x, self.fitness_history
# 运行遗传算法
if __name__ == "__main__":
ga = GeneticAlgorithm()
best_fitness, best_x, fitness_history = ga.run()
print(f"\n最优解: x = {best_x}, f(x) = {best_fitness}")
# 绘制适应度变化曲线
plt.figure(figsize=(10, 6))
plt.plot(fitness_history)
plt.title('平均适应度随迭代次数的变化')
plt.xlabel('迭代次数')
plt.ylabel('平均适应度')
plt.grid(True)
plt.show()
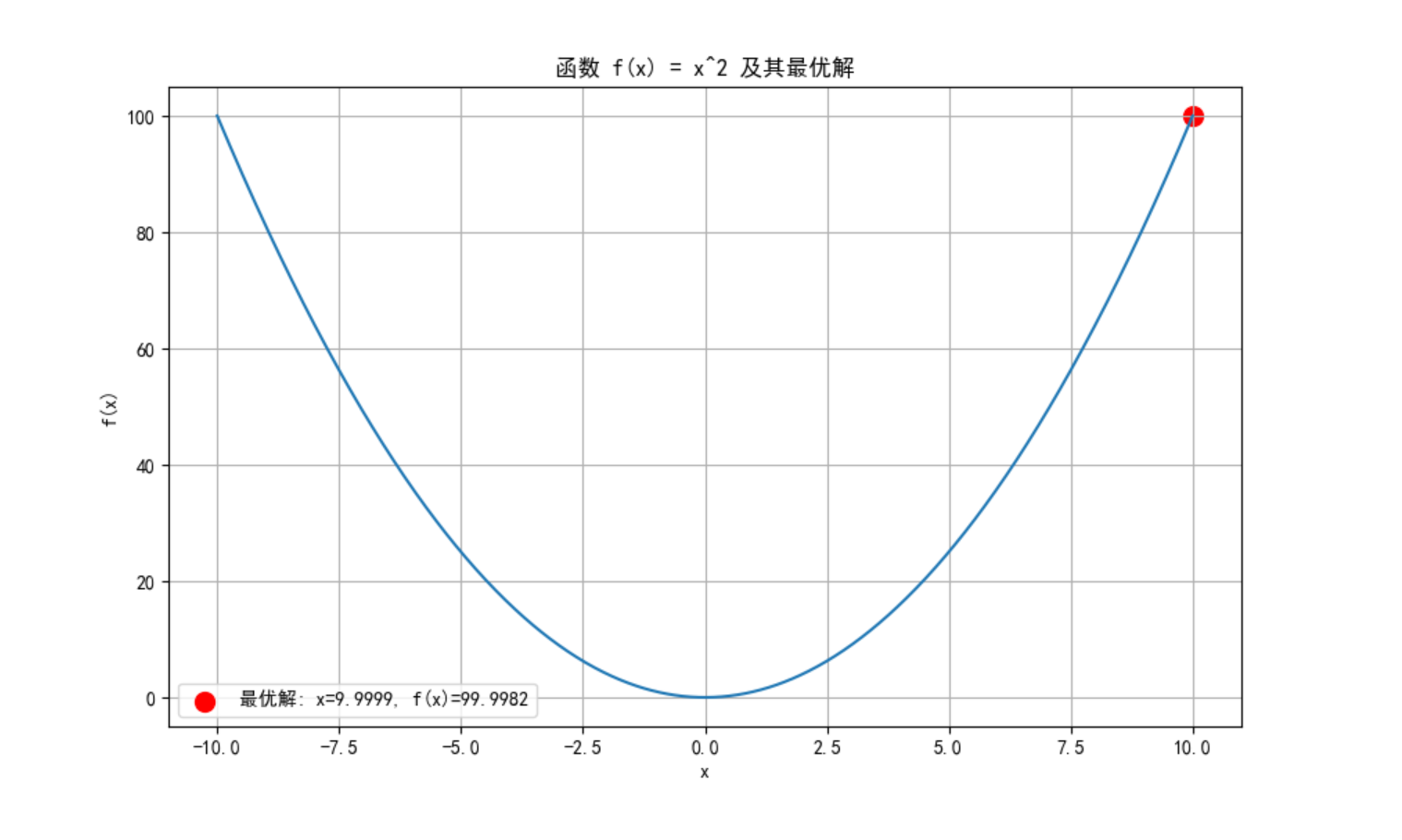
# 绘制函数图像和最优解
x = np.linspace(-10, 10, 1000)
y = x ** 2
plt.figure(figsize=(10, 6))
plt.plot(x, y)
plt.scatter(ga.best_x, ga.best_fitness, color='red', s=100,
label=f'最优解: x={ga.best_x:.4f}, f(x)={ga.best_fitness:.4f}')
plt.title('函数 f(x) = x^2 及其最优解')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True)
plt.show()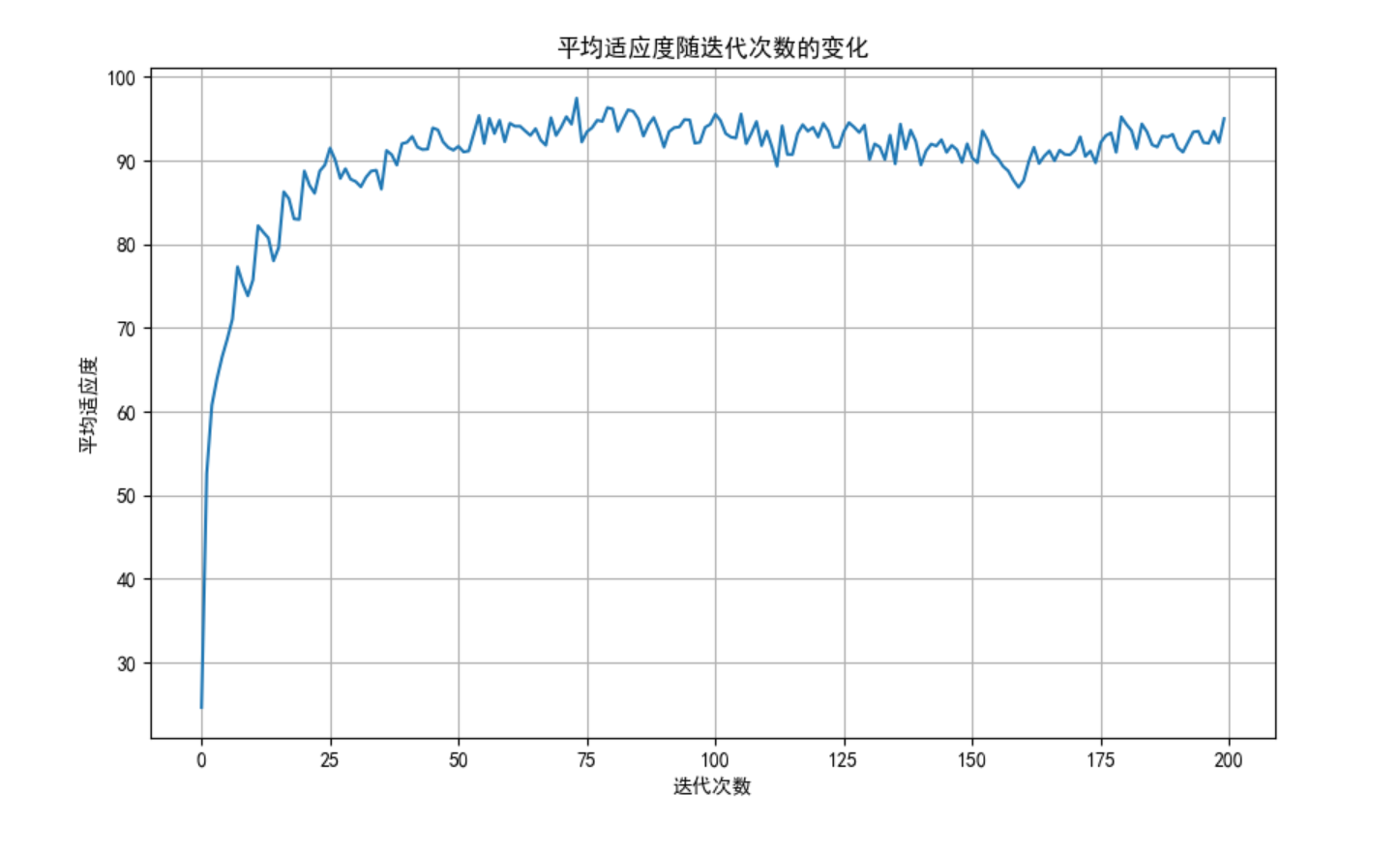
代码解析
上述代码实现了完整的基本遗传算法,主要包括以下几个部分:
- 初始化:设置种群大小、染色体长度、交叉变异概率等参数,并随机生成初始种群。
- 编码与解码:使用二进制编码表示变量 x,通过
decode_chromosome方法将二进制染色体解码为实数。 - 适应度函数:针对函数优化问题\(f(x)=x^2\),直接将函数值作为适应度。
- 选择操作:采用轮盘赌方法,根据适应度比例选择个体,适应度高的个体有更大概率被选中。
- 交叉操作:以一定概率对个体进行交叉,交换基因片段,生成新的个体。
- 变异操作:以低概率对个体的基因进行翻转,增加种群多样性。
- 迭代优化:通过多代进化,不断更新最优解,直到达到最大迭代次数。
6.3 遗传算法的改进算法
6.3.1 双倍体遗传算法
双倍体遗传算法模拟生物的双倍体染色体结构,每个基因座有两个等位基因(显性和隐性),通过显性规则决定表现型。
import numpy as np
import matplotlib.pyplot as plt
from typing import List, Tuple, Callable
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class GeneticAlgorithm:
def __init__(
self,
population_size: int = 100,
chromosome_length: int = 22,
max_generations: int = 200,
crossover_prob: float = 0.8,
mutation_prob: float = 0.01,
x_range: Tuple[float, float] = (-10, 10)
):
self.population_size = population_size
self.chromosome_length = chromosome_length
self.max_generations = max_generations
self.crossover_prob = crossover_prob
self.mutation_prob = mutation_prob
self.x_range = x_range
self.population = np.random.randint(0, 2, (population_size, chromosome_length))
self.best_fitness = 0
self.best_individual = None
self.best_x = 0
self.fitness_history = []
def decode_chromosome(self, chromosome: np.ndarray) -> float:
decimal = 0
for i, gene in enumerate(chromosome):
decimal += gene * (2 ** (self.chromosome_length - 1 - i))
x = self.x_range[0] + decimal * (self.x_range[1] - self.x_range[0]) / (2 ** self.chromosome_length - 1)
return x
def fitness_function(self, x: float) -> float:
return x ** 2
def calculate_fitness(self) -> np.ndarray:
fitness = np.zeros(self.population_size)
for i in range(self.population_size):
x = self.decode_chromosome(self.population[i])
fitness[i] = self.fitness_function(x)
if fitness[i] > self.best_fitness:
self.best_fitness = fitness[i]
self.best_individual = self.population[i].copy()
self.best_x = x
self.fitness_history.append(np.mean(fitness))
return fitness
def selection(self, fitness: np.ndarray) -> np.ndarray:
total_fitness = np.sum(fitness)
selection_probs = fitness / total_fitness
cumulative_probs = np.cumsum(selection_probs)
new_population = np.zeros((self.population_size, self.chromosome_length), dtype=int)
for i in range(self.population_size):
r = np.random.random()
for j in range(self.population_size):
if r <= cumulative_probs[j]:
new_population[i] = self.population[j].copy()
break
return new_population
def crossover(self, population: np.ndarray) -> np.ndarray:
new_population = population.copy()
for i in range(0, self.population_size, 2):
if i + 1 < self.population_size and np.random.random() < self.crossover_prob:
crossover_point = np.random.randint(1, self.chromosome_length)
new_population[i, crossover_point:], new_population[i + 1, crossover_point:] = \
new_population[i + 1, crossover_point:].copy(), new_population[i, crossover_point:].copy()
return new_population
def mutation(self, population: np.ndarray) -> np.ndarray:
for i in range(self.population_size):
for j in range(self.chromosome_length):
if np.random.random() < self.mutation_prob:
population[i, j] = 1 - population[i, j]
return population
def run(self) -> Tuple[float, float, List[float]]:
for generation in range(self.max_generations):
fitness = self.calculate_fitness()
population = self.selection(fitness)
population = self.crossover(population)
population = self.mutation(population)
self.population = population
if generation % 10 == 0:
print(f"Generation {generation}, Best fitness: {self.best_fitness}, Best x: {self.best_x}")
return self.best_fitness, self.best_x, self.fitness_history
class DiploidGeneticAlgorithm(GeneticAlgorithm):
def __init__(self, *args, dominance_degree: float = 0.5, **kwargs):
super().__init__(*args, **kwargs)
self.dominance_degree = dominance_degree
self.population = np.random.randint(0, 2, (self.population_size, 2, self.chromosome_length))
def decode_chromosome(self, chromosome: np.ndarray) -> float:
"""双倍体染色体解码"""
dominant = chromosome[0]
recessive = chromosome[1]
decimal_dominant = 0
decimal_recessive = 0
for i, (d_gene, r_gene) in enumerate(zip(dominant, recessive)):
decimal_dominant += d_gene * (2 ** (self.chromosome_length - 1 - i))
decimal_recessive += r_gene * (2 ** (self.chromosome_length - 1 - i))
decimal = decimal_dominant * self.dominance_degree + decimal_recessive * (1 - self.dominance_degree)
x = self.x_range[0] + decimal * (self.x_range[1] - self.x_range[0]) / (2 ** self.chromosome_length - 1)
return x
def selection(self, fitness: np.ndarray) -> np.ndarray:
"""双倍体选择操作"""
total_fitness = np.sum(fitness)
selection_probs = fitness / total_fitness
cumulative_probs = np.cumsum(selection_probs)
new_population = np.zeros((self.population_size, 2, self.chromosome_length), dtype=int)
for i in range(self.population_size):
r = np.random.random()
for j in range(self.population_size):
if r <= cumulative_probs[j]:
new_population[i] = self.population[j].copy()
break
return new_population
def crossover(self, population: np.ndarray) -> np.ndarray:
"""双倍体交叉操作"""
new_population = population.copy()
for i in range(0, self.population_size, 2):
if i + 1 < self.population_size and np.random.random() < self.crossover_prob:
crossover_point = np.random.randint(1, self.chromosome_length)
# 分别交叉显性和隐性染色体
new_population[i, 0, crossover_point:], new_population[i + 1, 0, crossover_point:] = \
new_population[i + 1, 0, crossover_point:].copy(), new_population[i, 0, crossover_point:].copy()
new_population[i, 1, crossover_point:], new_population[i + 1, 1, crossover_point:] = \
new_population[i + 1, 1, crossover_point:].copy(), new_population[i, 1, crossover_point:].copy()
return new_population
def mutation(self, population: np.ndarray) -> np.ndarray:
"""双倍体变异操作"""
for i in range(self.population_size):
for j in range(2): # 对显性和隐性基因都进行变异
for k in range(self.chromosome_length):
if np.random.random() < self.mutation_prob:
population[i, j, k] = 1 - population[i, j, k]
return population
# 测试代码
if __name__ == "__main__":
ga = DiploidGeneticAlgorithm(population_size=50, max_generations=50)
best_fitness, best_x, fitness_history = ga.run()
print(f"\n最优解: x = {best_x:.4f}, f(x) = {best_fitness:.4f}")
# 绘制适应度变化曲线
plt.figure(figsize=(10, 6))
plt.plot(fitness_history)
plt.title('双倍体遗传算法 - 平均适应度变化')
plt.xlabel('迭代次数')
plt.ylabel('平均适应度')
plt.grid(True)
plt.show()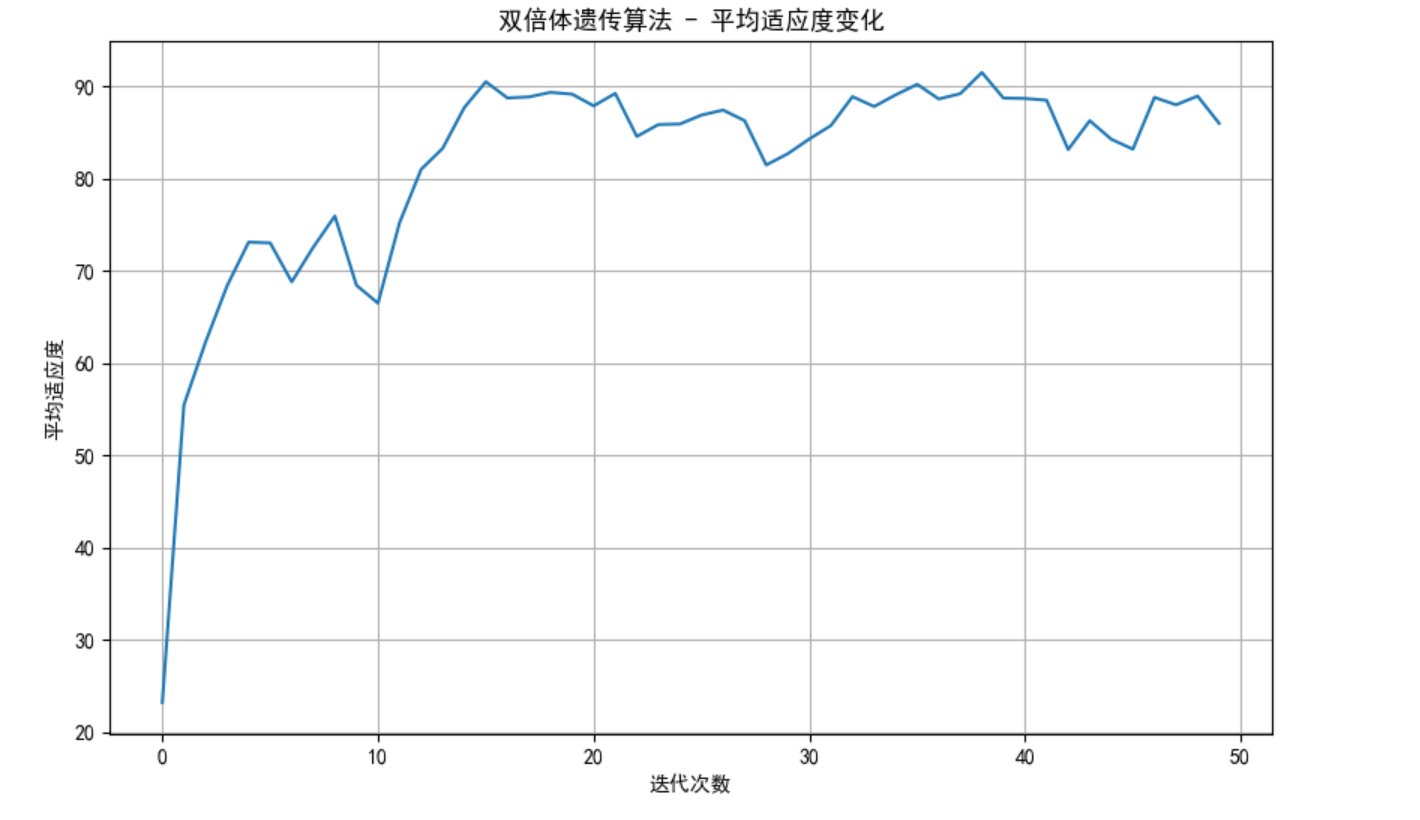
6.3.2 双种群遗传算法
双种群遗传算法包含两个种群:全局探索种群和局部开发种群,通过移民操作交换个体。
import numpy as np
import matplotlib.pyplot as plt
from typing import Tuple, Callable
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class GeneticAlgorithm:
def __init__(
self,
population_size: int = 100,
chromosome_length: int = 22,
max_generations: int = 200,
crossover_prob: float = 0.8,
mutation_prob: float = 0.01,
x_range: Tuple[float, float] = (-10, 10)
):
"""基础遗传算法实现"""
self.population_size = population_size
self.chromosome_length = chromosome_length
self.max_generations = max_generations
self.crossover_prob = crossover_prob
self.mutation_prob = mutation_prob
self.x_range = x_range
self.population = np.random.randint(0, 2, (population_size, chromosome_length))
self.best_fitness = 0
self.best_x = 0
self.fitness_history = []
def decode_chromosome(self, chromosome: np.ndarray) -> float:
"""二进制染色体解码为实数"""
decimal = sum(gene * (2 ** (self.chromosome_length - 1 - i))
for i, gene in enumerate(chromosome))
return self.x_range[0] + decimal * (self.x_range[1] - self.x_range[0]) / (2 ** self.chromosome_length - 1)
def fitness_function(self, x: float) -> float:
"""目标函数 f(x) = x^2"""
return x ** 2
def calculate_fitness(self) -> np.ndarray:
"""计算种群适应度并更新最优解"""
fitness = np.array([self.fitness_function(self.decode_chromosome(ind))
for ind in self.population])
best_idx = np.argmax(fitness)
if fitness[best_idx] > self.best_fitness:
self.best_fitness = fitness[best_idx]
self.best_x = self.decode_chromosome(self.population[best_idx])
self.fitness_history.append(np.mean(fitness))
return fitness
def selection(self, fitness: np.ndarray) -> np.ndarray:
"""轮盘赌选择操作"""
total_fitness = np.sum(fitness)
probs = fitness / total_fitness
cum_probs = np.cumsum(probs)
new_pop = np.zeros((self.population_size, self.chromosome_length), dtype=int)
for i in range(self.population_size):
r = np.random.random()
for j in range(self.population_size):
if r <= cum_probs[j]:
new_pop[i] = self.population[j].copy()
break
return new_pop
def crossover(self, population: np.ndarray) -> np.ndarray:
"""单点交叉操作"""
new_pop = population.copy()
for i in range(0, self.population_size, 2):
if i + 1 < self.population_size and np.random.random() < self.crossover_prob:
point = np.random.randint(1, self.chromosome_length)
new_pop[i, point:], new_pop[i + 1, point:] = new_pop[i + 1, point:].copy(), new_pop[i, point:].copy()
return new_pop
def mutation(self, population: np.ndarray) -> np.ndarray:
"""基因变异操作"""
for i in range(self.population_size):
for j in range(self.chromosome_length):
if np.random.random() < self.mutation_prob:
population[i, j] = 1 - population[i, j]
return population
def run(self) -> Tuple[float, float]:
"""执行遗传算法迭代"""
for gen in range(self.max_generations):
fitness = self.calculate_fitness()
self.population = self.mutation(self.crossover(self.selection(fitness)))
if gen % 10 == 0:
print(f"GA代{gen} | 最优适应度: {self.best_fitness:.2f} | x: {self.best_x:.2f}")
return self.best_fitness, self.best_x
class DiploidGeneticAlgorithm(GeneticAlgorithm):
def __init__(self, *args, dominance_degree: float = 0.5, **kwargs):
"""双倍体遗传算法(继承基础GA)"""
super().__init__(*args, **kwargs)
self.dominance_degree = dominance_degree
self.population = np.random.randint(0, 2, (self.population_size, 2, self.chromosome_length))
def decode_chromosome(self, chromosome: np.ndarray) -> float:
"""双倍体解码(考虑显性/隐性基因)"""
dominant, recessive = chromosome
d_dec = sum(gene * (2 ** (self.chromosome_length - 1 - i)) for i, gene in enumerate(dominant))
r_dec = sum(gene * (2 ** (self.chromosome_length - 1 - i)) for i, gene in enumerate(recessive))
dec = d_dec * self.dominance_degree + r_dec * (1 - self.dominance_degree)
return self.x_range[0] + dec * (self.x_range[1] - self.x_range[0]) / (2 ** self.chromosome_length - 1)
def selection(self, fitness: np.ndarray) -> np.ndarray:
"""双倍体选择(三维数组处理)"""
total_fitness = np.sum(fitness)
probs = fitness / total_fitness
cum_probs = np.cumsum(probs)
new_pop = np.zeros((self.population_size, 2, self.chromosome_length), dtype=int)
for i in range(self.population_size):
r = np.random.random()
for j in range(self.population_size):
if r <= cum_probs[j]:
new_pop[i] = self.population[j].copy()
break
return new_pop
def crossover(self, population: np.ndarray) -> np.ndarray:
"""双倍体交叉(显性/隐性基因分别交叉)"""
new_pop = population.copy()
for i in range(0, self.population_size, 2):
if i + 1 < self.population_size and np.random.random() < self.crossover_prob:
point = np.random.randint(1, self.chromosome_length)
# 显性基因交叉
new_pop[i, 0, point:], new_pop[i + 1, 0, point:] = new_pop[i + 1, 0, point:].copy(), new_pop[i, 0,
point:].copy()
# 隐性基因交叉
new_pop[i, 1, point:], new_pop[i + 1, 1, point:] = new_pop[i + 1, 1, point:].copy(), new_pop[i, 1,
point:].copy()
return new_pop
def mutation(self, population: np.ndarray) -> np.ndarray:
"""双倍体变异(双基因链变异)"""
for i in range(self.population_size):
for j in range(2):
for k in range(self.chromosome_length):
if np.random.random() < self.mutation_prob:
population[i, j, k] = 1 - population[i, j, k]
return population
class DualPopulationGA:
def __init__(
self,
population_size: int = 100,
chromosome_length: int = 22,
max_generations: int = 200,
migration_rate: float = 0.1,
migration_interval: int = 10,
use_diploid: bool = False,
dominance_degree: float = 0.5,
x_range: Tuple[float, float] = (-10, 10)
):
"""双种群遗传算法主类
参数:
use_diploid: 是否启用双倍体子种群
dominance_degree: 双倍体显性度
"""
self.population_size = population_size
self.max_generations = max_generations
self.migration_rate = migration_rate
self.migration_interval = migration_interval
self.best_fitness = 0
self.best_x = 0
# 选择子种群类型(普通GA或双倍体GA)
GA_CLASS = DiploidGeneticAlgorithm if use_diploid else GeneticAlgorithm
# 初始化双种群:探索种群(高变异)和开发种群(低变异)
self.exploration_pop = GA_CLASS(
population_size, chromosome_length, max_generations,
crossover_prob=0.8, mutation_prob=0.02, x_range=x_range
)
if use_diploid:
self.exploration_pop.dominance_degree = dominance_degree
self.exploitation_pop = GA_CLASS(
population_size, chromosome_length, max_generations,
crossover_prob=0.8, mutation_prob=0.005, x_range=x_range
)
if use_diploid:
self.exploitation_pop.dominance_degree = dominance_degree
# 合并双种群适应度历史(用于可视化)
self.fitness_history = []
def _migrate(self):
"""双种群移民操作"""
migrate_num = int(self.population_size * self.migration_rate)
if migrate_num == 0:
return
# 探索种群→开发种群移民
exp_fitness = self.exploration_pop.calculate_fitness()
exp_best = np.argsort(exp_fitness)[-migrate_num:]
exp_migrants = self.exploration_pop.population[exp_best]
# 替换开发种群中的随机个体
exploit_replace = np.random.choice(self.population_size, migrate_num, replace=False)
self.exploitation_pop.population[exploit_replace] = exp_migrants
# 开发种群→探索种群移民
exploit_fitness = self.exploitation_pop.calculate_fitness()
exploit_best = np.argsort(exploit_fitness)[-migrate_num:]
exploit_migrants = self.exploitation_pop.population[exploit_best]
# 替换探索种群中的随机个体
exp_replace = np.random.choice(self.population_size, migrate_num, replace=False)
self.exploration_pop.population[exp_replace] = exploit_migrants
def run(self) -> Tuple[float, float]:
"""执行双种群迭代优化"""
for gen in range(self.max_generations):
# 双种群独立进化
self.exploration_pop.calculate_fitness()
self.exploitation_pop.calculate_fitness()
# 更新全局最优解
for pop in [self.exploration_pop, self.exploitation_pop]:
if pop.best_fitness > self.best_fitness:
self.best_fitness = pop.best_fitness
self.best_x = pop.best_x
# 记录平均适应度
avg_fitness = (np.mean(self.exploration_pop.fitness_history[-1:]) +
np.mean(self.exploitation_pop.fitness_history[-1:])) / 2
self.fitness_history.append(avg_fitness)
# 执行移民操作
if gen % self.migration_interval == 0 and gen > 0:
self._migrate()
if gen % 10 == 0:
print(f"双种群代{gen} | 全局最优: f({self.best_x:.2f})={self.best_fitness:.2f}")
return self.best_fitness, self.best_x
def plot_fitness(self):
"""绘制适应度进化曲线"""
plt.figure(figsize=(10, 6))
plt.plot(self.fitness_history)
plt.title('双种群遗传算法适应度进化曲线')
plt.xlabel('迭代次数')
plt.ylabel('平均适应度')
plt.grid(True)
plt.show()
# 主程序:测试双种群算法
if __name__ == "__main__":
# 1. 测试普通双种群遗传算法
print("=== 普通双种群遗传算法 ===")
dual_ga = DualPopulationGA(
population_size=50,
max_generations=100,
migration_rate=0.1,
use_diploid=False
)
best_fitness, best_x = dual_ga.run()
print(f"最优解: x = {best_x:.4f}, f(x) = {best_fitness:.4f}")
dual_ga.plot_fitness()
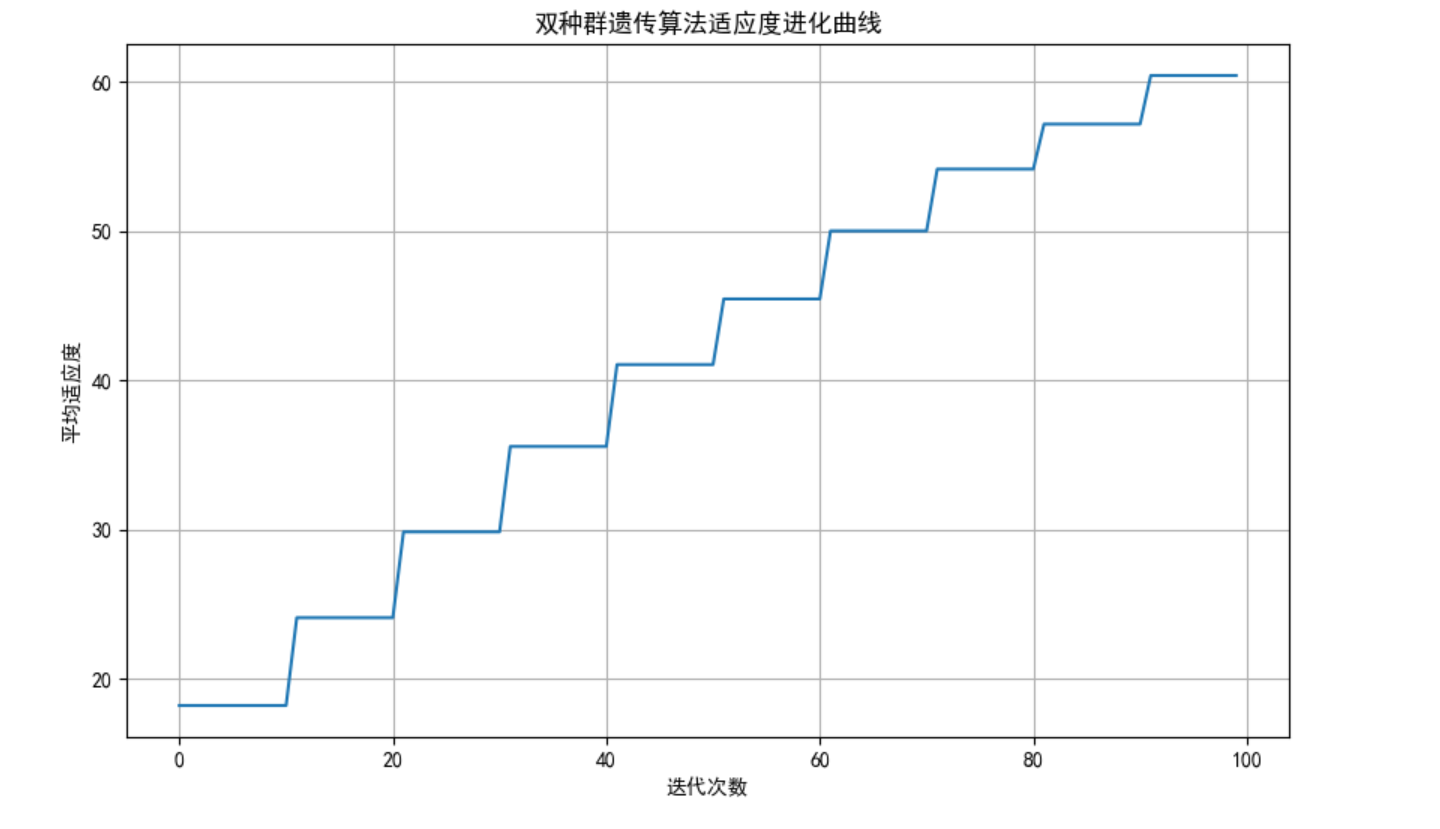
# 2. 测试双倍体双种群遗传算法
print("\n=== 双倍体双种群遗传算法 ===")
dual_diploid_ga = DualPopulationGA(
population_size=50,
max_generations=100,
migration_rate=0.1,
use_diploid=True,
dominance_degree=0.7
)
best_fitness, best_x = dual_diploid_ga.run()
print(f"最优解: x = {best_x:.4f}, f(x) = {best_fitness:.4f}")
dual_diploid_ga.plot_fitness()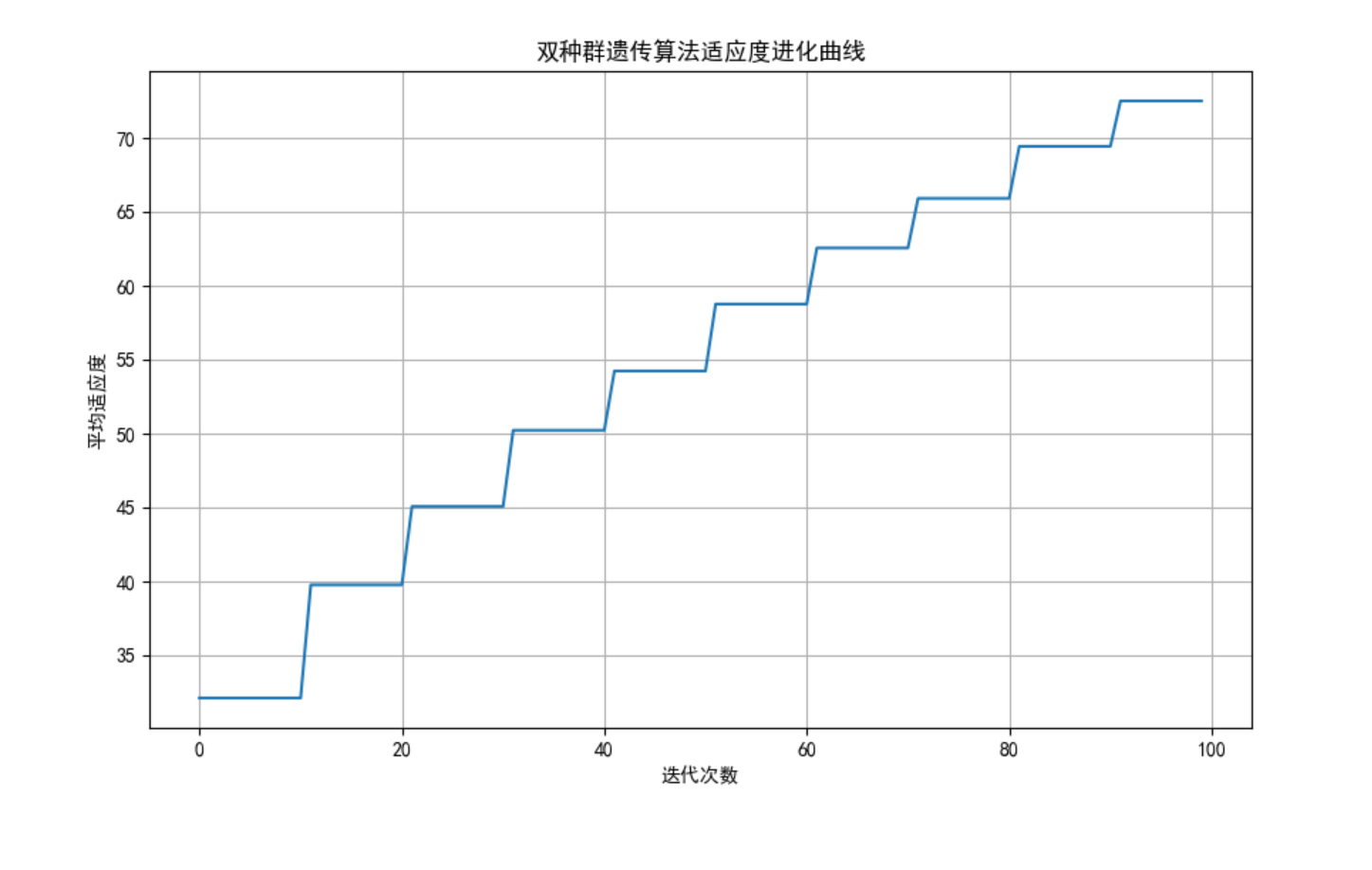
6.3.3 自适应遗传算法
自适应遗传算法根据个体适应度自动调整交叉和变异概率,避免早熟收敛。
import numpy as np
import matplotlib.pyplot as plt
from typing import Tuple, List
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class GeneticAlgorithm:
def __init__(
self,
population_size: int = 100,
chromosome_length: int = 22,
max_generations: int = 200,
crossover_prob: float = 0.8,
mutation_prob: float = 0.01,
x_range: Tuple[float, float] = (-10, 10)
):
"""基础遗传算法实现"""
self.population_size = population_size
self.chromosome_length = chromosome_length
self.max_generations = max_generations
self.crossover_prob = crossover_prob
self.mutation_prob = mutation_prob
self.x_range = x_range
self.population = np.random.randint(0, 2, (population_size, chromosome_length))
self.best_fitness = 0
self.best_x = 0
self.fitness_history = []
def decode_chromosome(self, chromosome: np.ndarray) -> float:
"""二进制染色体解码为实数"""
decimal = sum(gene * (2 ** (self.chromosome_length - 1 - i))
for i, gene in enumerate(chromosome))
return self.x_range[0] + decimal * (self.x_range[1] - self.x_range[0]) / (2 ** self.chromosome_length - 1)
def fitness_function(self, x: float) -> float:
"""目标函数 f(x) = x^2"""
return x ** 2
def calculate_fitness(self) -> np.ndarray:
"""计算种群适应度并更新最优解"""
fitness = np.array([self.fitness_function(self.decode_chromosome(ind))
for ind in self.population])
best_idx = np.argmax(fitness)
if fitness[best_idx] > self.best_fitness:
self.best_fitness = fitness[best_idx]
self.best_x = self.decode_chromosome(self.population[best_idx])
self.fitness_history.append(np.mean(fitness))
return fitness
def selection(self, fitness: np.ndarray) -> np.ndarray:
"""轮盘赌选择操作"""
total_fitness = np.sum(fitness)
probs = fitness / total_fitness
cum_probs = np.cumsum(probs)
new_pop = np.zeros((self.population_size, self.chromosome_length), dtype=int)
for i in range(self.population_size):
r = np.random.random()
for j in range(self.population_size):
if r <= cum_probs[j]:
new_pop[i] = self.population[j].copy()
break
return new_pop
def crossover(self, population: np.ndarray) -> np.ndarray:
"""单点交叉操作"""
new_pop = population.copy()
for i in range(0, self.population_size, 2):
if i + 1 < self.population_size and np.random.random() < self.crossover_prob:
point = np.random.randint(1, self.chromosome_length)
new_pop[i, point:], new_pop[i + 1, point:] = new_pop[i + 1, point:].copy(), new_pop[i, point:].copy()
return new_pop
def mutation(self, population: np.ndarray) -> np.ndarray:
"""基因变异操作"""
for i in range(self.population_size):
for j in range(self.chromosome_length):
if np.random.random() < self.mutation_prob:
population[i, j] = 1 - population[i, j]
return population
def run(self) -> Tuple[float, float, List[float]]:
"""执行遗传算法迭代"""
for gen in range(self.max_generations):
fitness = self.calculate_fitness()
self.population = self.mutation(self.crossover(self.selection(fitness)))
if gen % 10 == 0:
print(f"GA代{gen} | 最优适应度: {self.best_fitness:.2f} | x: {self.best_x:.2f}")
return self.best_fitness, self.best_x, self.fitness_history
class AdaptiveGeneticAlgorithm(GeneticAlgorithm):
def __init__(self, *args, c1: float = 0.9, c2: float = 0.6, m1: float = 0.1, m2: float = 0.001, **kwargs):
"""
自适应遗传算法
参数:
c1, c2: 交叉概率参数
m1, m2: 变异概率参数
"""
super().__init__(*args, **kwargs)
self.c1 = c1 # 最大交叉概率
self.c2 = c2 # 最小交叉概率
self.m1 = m1 # 最大变异概率
self.m2 = m2 # 最小变异概率
def calculate_adaptive_probs(self, fitness: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:
"""
计算自适应交叉和变异概率
返回:
crossover_probs: 每个个体的交叉概率
mutation_probs: 每个个体的变异概率
"""
avg_fitness = np.mean(fitness)
max_fitness = np.max(fitness)
# 初始化概率数组
crossover_probs = np.zeros_like(fitness, dtype=float)
mutation_probs = np.zeros_like(fitness, dtype=float)
# 计算每个个体的自适应概率
for i in range(len(fitness)):
# 自适应交叉概率
if fitness[i] >= avg_fitness:
# 高适应度个体: 较低的交叉概率,保护优良解
crossover_probs[i] = self.c2 - (self.c2 - 0.4) * (fitness[i] - avg_fitness) / (
max_fitness - avg_fitness)
else:
# 低适应度个体: 较高的交叉概率,促进探索
crossover_probs[i] = self.c1
# 自适应变异概率
if fitness[i] >= avg_fitness:
# 高适应度个体: 较低的变异概率,保护优良解
mutation_probs[i] = self.m2 - (self.m2 - 0.001) * (fitness[i] - avg_fitness) / (
max_fitness - avg_fitness)
else:
# 低适应度个体: 较高的变异概率,增加多样性
mutation_probs[i] = self.m1
# 确保概率在合理范围内
crossover_probs = np.clip(crossover_probs, 0.4, 0.9)
mutation_probs = np.clip(mutation_probs, 0.001, 0.1)
return crossover_probs, mutation_probs
def crossover(self, population: np.ndarray, fitness: np.ndarray) -> np.ndarray:
"""自适应交叉操作"""
new_population = population.copy()
crossover_probs, _ = self.calculate_adaptive_probs(fitness)
for i in range(0, self.population_size, 2):
if i + 1 < self.population_size:
# 使用父代中较高适应度的个体来确定交叉概率
parent_idx = i if fitness[i] > fitness[i + 1] else i + 1
if np.random.random() < crossover_probs[parent_idx]:
# 执行单点交叉
crossover_point = np.random.randint(1, self.chromosome_length)
new_population[i, crossover_point:], new_population[i + 1, crossover_point:] = \
new_population[i + 1, crossover_point:].copy(), new_population[i, crossover_point:].copy()
return new_population
def mutation(self, population: np.ndarray, fitness: np.ndarray) -> np.ndarray:
"""自适应变异操作"""
_, mutation_probs = self.calculate_adaptive_probs(fitness)
for i in range(self.population_size):
for j in range(self.chromosome_length):
if np.random.random() < mutation_probs[i]:
# 执行变异
population[i, j] = 1 - population[i, j]
return population
def run(self) -> Tuple[float, float, List[float]]:
"""运行自适应遗传算法"""
for generation in range(self.max_generations):
fitness = self.calculate_fitness()
population = self.selection(fitness)
population = self.crossover(population, fitness)
population = self.mutation(population, fitness)
self.population = population
if generation % 10 == 0:
print(
f"Adaptive GA Generation {generation} | Best fitness: {self.best_fitness:.2f} | Best x: {self.best_x:.2f}")
return self.best_fitness, self.best_x, self.fitness_history
def plot_fitness(self):
"""绘制适应度进化曲线"""
plt.figure(figsize=(10, 6))
plt.plot(self.fitness_history)
plt.title('自适应遗传算法适应度进化曲线')
plt.xlabel('迭代次数')
plt.ylabel('平均适应度')
plt.grid(True)
plt.show()
# 主程序:测试自适应遗传算法
if __name__ == "__main__":
print("=== 自适应遗传算法 ===")
adaptive_ga = AdaptiveGeneticAlgorithm(
population_size=50,
max_generations=100,
x_range=(-10, 10)
)
best_fitness, best_x, _ = adaptive_ga.run()
print(f"最优解: x = {best_x:.4f}, f(x) = {best_fitness:.4f}")
# 绘制适应度进化曲线
adaptive_ga.plot_fitness()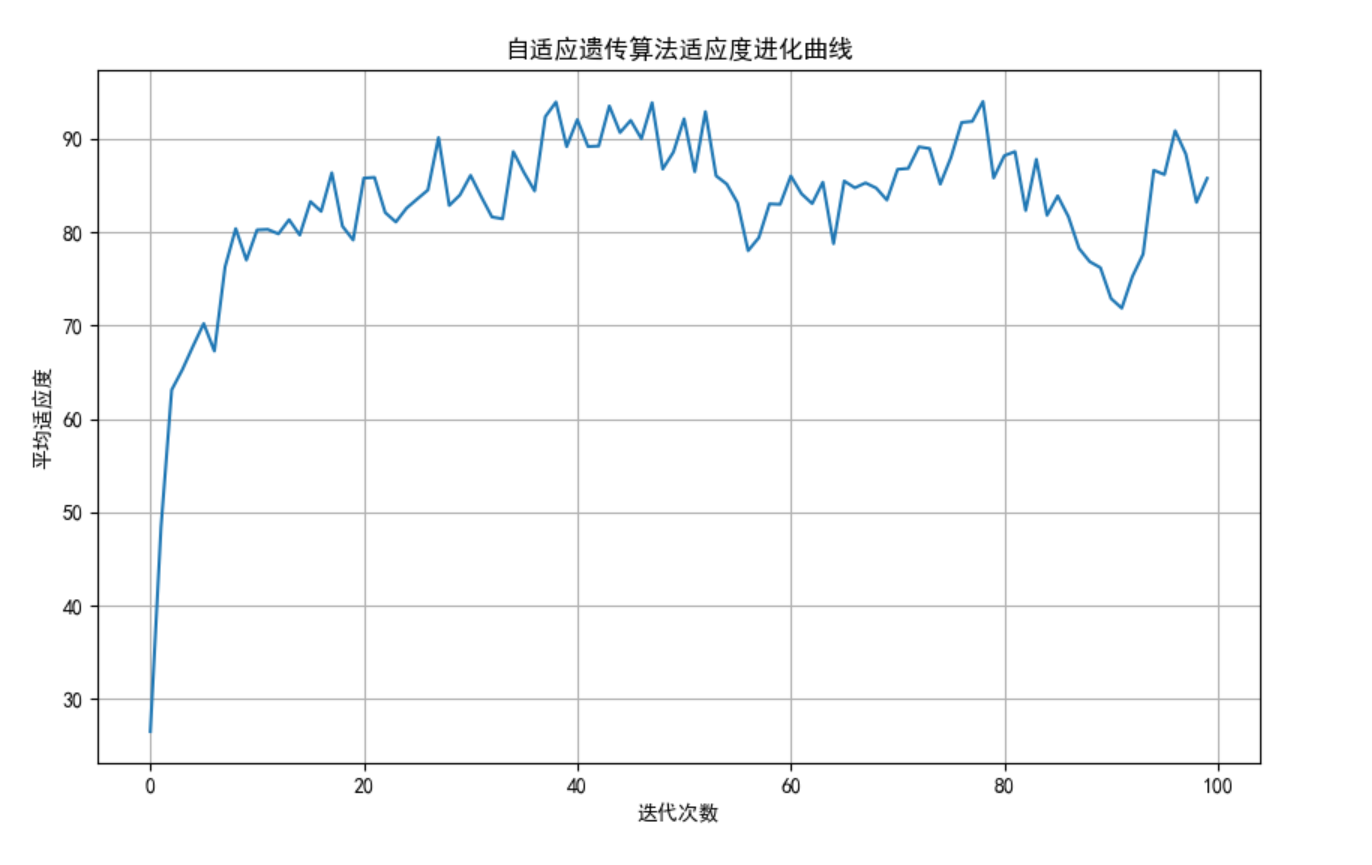
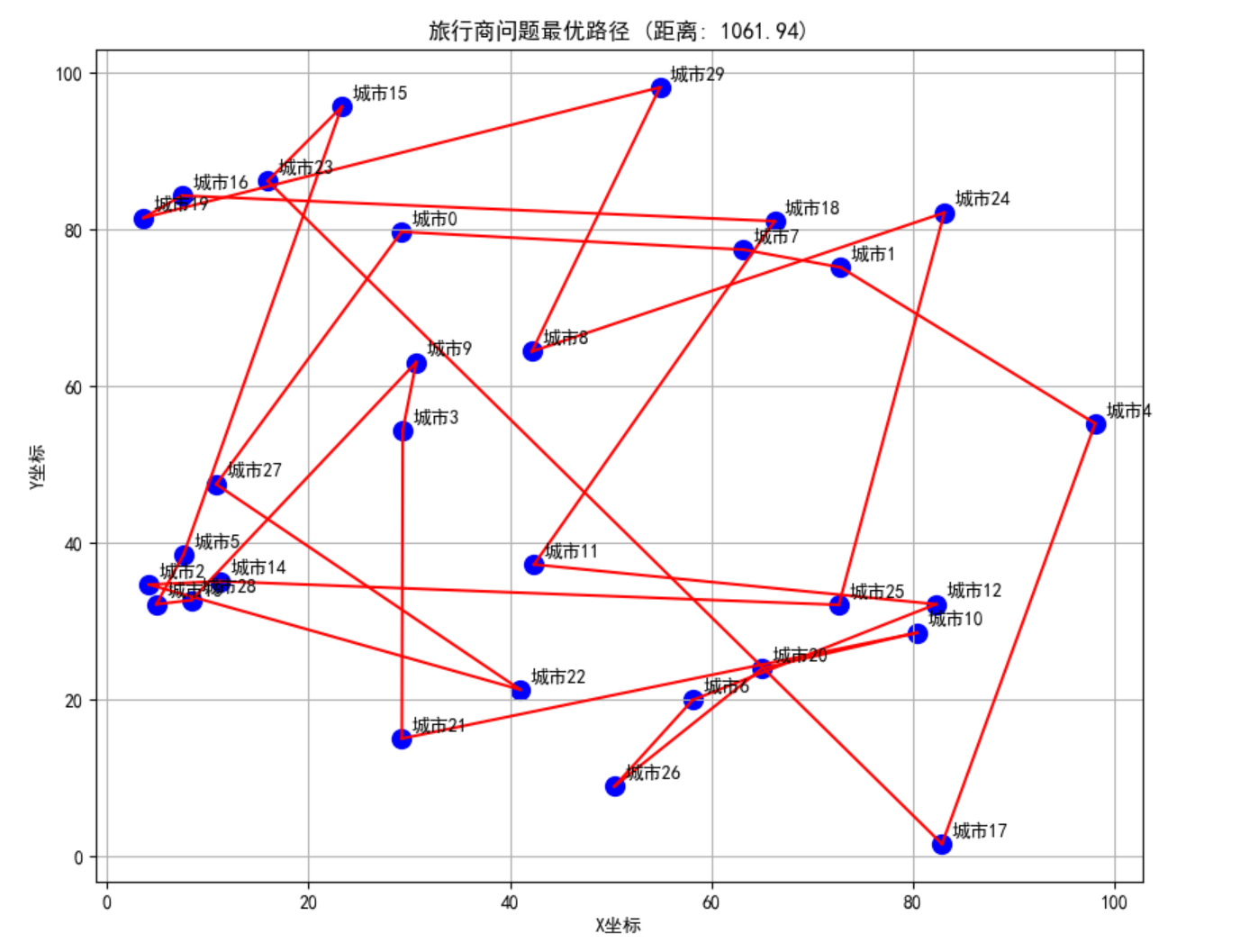
6.4 遗传算法的应用
遗传算法在多个领域有广泛应用,以下是一个旅行商问题 (TSP) 的应用案例:
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
from typing import Tuple, List
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class TSPSolver:
def __init__(
self,
city_num: int = 20,
population_size: int = 100,
max_generations: int = 200,
crossover_prob: float = 0.8,
mutation_prob: float = 0.1
):
"""
旅行商问题遗传算法求解器
参数:
city_num: 城市数量
population_size: 种群大小
max_generations: 最大迭代次数
crossover_prob: 交叉概率
mutation_prob: 变异概率
"""
self.city_num = city_num
self.population_size = population_size
self.max_generations = max_generations
self.crossover_prob = crossover_prob
self.mutation_prob = mutation_prob
# 随机生成城市坐标
self.cities = np.random.rand(city_num, 2) * 100
# 初始化种群: 每个个体是城市索引的排列
self.population = np.array([np.random.permutation(city_num) for _ in range(population_size)])
self.best_path = None
self.best_distance = float('inf')
self.distance_history = []
def calculate_distance(self, path: np.ndarray) -> float:
"""计算路径总距离"""
distance = 0
for i in range(self.city_num - 1):
distance += np.sqrt(np.sum((self.cities[path[i]] - self.cities[path[i + 1]]) ** 2))
# 回到起点
distance += np.sqrt(np.sum((self.cities[path[-1]] - self.cities[path[0]]) ** 2))
return distance
def fitness_function(self, path: np.ndarray) -> float:
"""适应度函数: 距离的倒数"""
distance = self.calculate_distance(path)
# 避免除零错误
return 1.0 / (distance + 1e-10)
def selection(self, fitness: np.ndarray) -> np.ndarray:
"""轮盘赌选择"""
total_fitness = np.sum(fitness)
selection_probs = fitness / total_fitness
cumulative_probs = np.cumsum(selection_probs)
new_population = np.zeros((self.population_size, self.city_num), dtype=int)
for i in range(self.population_size):
r = np.random.random()
for j in range(self.population_size):
if r <= cumulative_probs[j]:
new_population[i] = self.population[j].copy()
break
return new_population
def order_crossover(self, parent1: np.ndarray, parent2: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:
"""顺序交叉(OX)"""
child1 = np.zeros(self.city_num, dtype=int)
child2 = np.zeros(self.city_num, dtype=int)
# 随机选择交叉点
point1, point2 = np.random.choice(self.city_num, 2, replace=False)
if point1 > point2:
point1, point2 = point2, point1
# 保留父代1在交叉点之间的部分
child1[point1:point2 + 1] = parent1[point1:point2 + 1]
# 保留父代2在交叉点之间的部分
child2[point1:point2 + 1] = parent2[point1:point2 + 1]
# 填充剩余部分 - 修正后的实现
def fill_remaining(parent, child, start, end):
remaining = []
# 收集父代中未在子代中的城市
for city in parent:
if city not in child[start:end + 1]:
remaining.append(city)
# 填充剩余位置
idx = 0
for i in range(self.city_num):
if i < start or i > end:
child[i] = remaining[idx]
idx += 1
return child
# 填充子代1
child1 = fill_remaining(parent2, child1, point1, point2)
# 填充子代2
child2 = fill_remaining(parent1, child2, point1, point2)
return child1, child2
def crossover(self, population: np.ndarray) -> np.ndarray:
"""交叉操作"""
new_population = population.copy()
for i in range(0, self.population_size, 2):
if i + 1 < self.population_size and np.random.random() < self.crossover_prob:
child1, child2 = self.order_crossover(population[i], population[i + 1])
new_population[i] = child1
new_population[i + 1] = child2
return new_population
def mutation(self, population: np.ndarray) -> np.ndarray:
"""变异操作: 交换变异"""
for i in range(self.population_size):
if np.random.random() < self.mutation_prob:
# 随机选择两个位置交换
pos1, pos2 = np.random.choice(self.city_num, 2, replace=False)
population[i, pos1], population[i, pos2] = population[i, pos2], population[i, pos1]
return population
def run(self) -> Tuple[np.ndarray, float, List[float]]:
"""运行算法"""
for generation in range(self.max_generations):
# 计算适应度
fitness = np.array([self.fitness_function(path) for path in self.population])
# 计算平均距离
avg_distance = np.mean([self.calculate_distance(path) for path in self.population])
self.distance_history.append(avg_distance)
# 更新最优解
for path in self.population:
distance = self.calculate_distance(path)
if distance < self.best_distance:
self.best_distance = distance
self.best_path = path.copy()
# 选择、交叉、变异
self.population = self.selection(fitness)
self.population = self.crossover(self.population)
self.population = self.mutation(self.population)
if generation % 10 == 0:
print(
f"Generation {generation}, Best distance: {self.best_distance:.2f}, Avg distance: {avg_distance:.2f}")
return self.best_path, self.best_distance, self.distance_history
def plot_solution(self):
"""绘制最优路径"""
if self.best_path is None:
print("请先运行算法获取最优路径")
return
plt.figure(figsize=(10, 8))
# 绘制城市
plt.scatter(self.cities[:, 0], self.cities[:, 1], c='blue', s=100)
for i, city in enumerate(self.cities):
plt.text(city[0] + 1, city[1] + 1, f'城市{i}', fontsize=10)
# 绘制最优路径
path = self.best_path
for i in range(self.city_num - 1):
plt.plot([self.cities[path[i], 0], self.cities[path[i + 1], 0]],
[self.cities[path[i], 1], self.cities[path[i + 1], 1]], 'r-')
# 回到起点
plt.plot([self.cities[path[-1], 0], self.cities[path[0], 0]],
[self.cities[path[-1], 1], self.cities[path[0], 1]], 'r-')
plt.title(f'旅行商问题最优路径 (距离: {self.best_distance:.2f})')
plt.xlabel('X坐标')
plt.ylabel('Y坐标')
plt.grid(True)
plt.show()
# 绘制距离变化曲线
plt.figure(figsize=(10, 6))
plt.plot(self.distance_history)
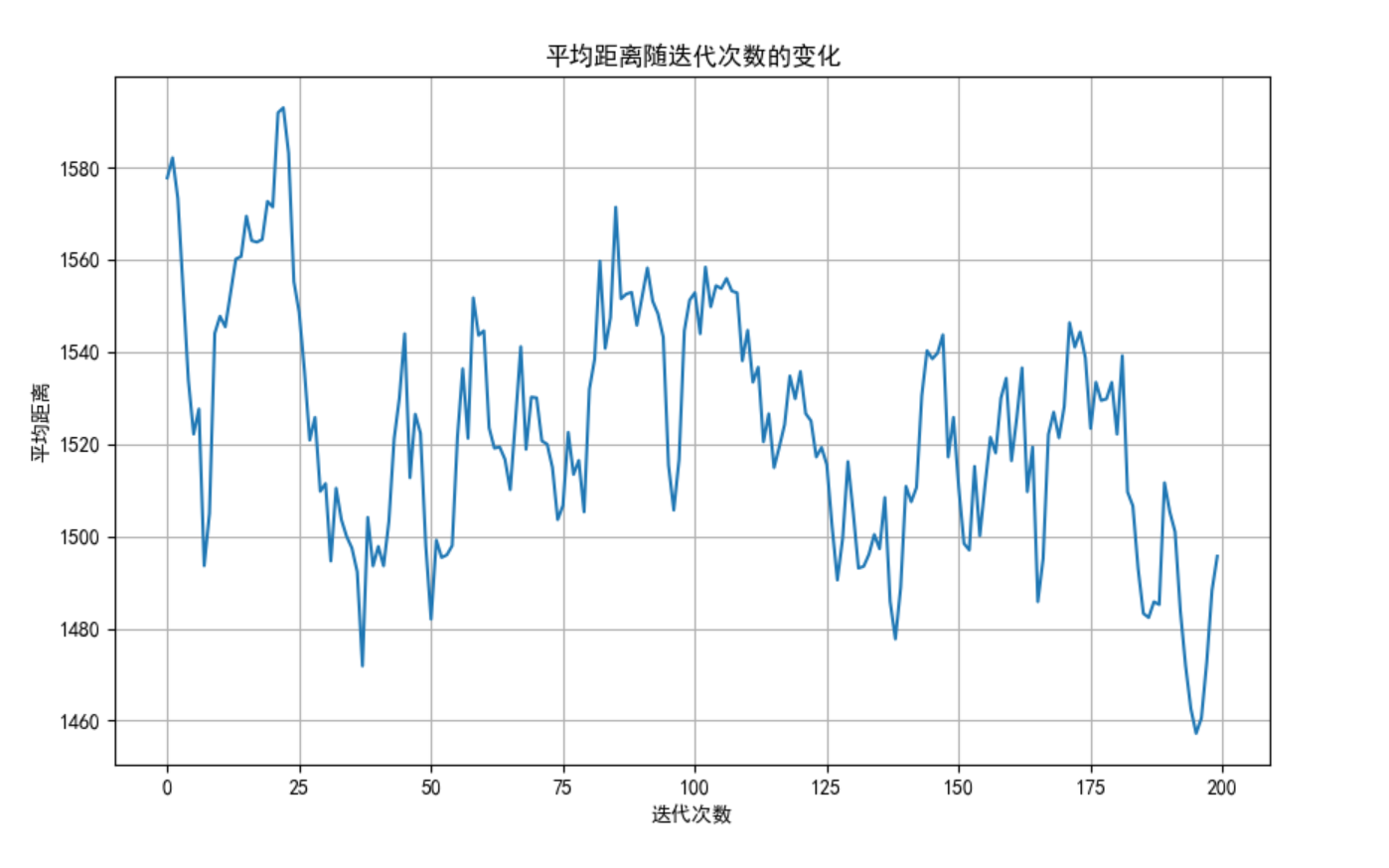
plt.title('平均距离随迭代次数的变化')
plt.xlabel('迭代次数')
plt.ylabel('平均距离')
plt.grid(True)
plt.show()
# 运行TSP求解器
if __name__ == "__main__":
tsp = TSPSolver(city_num=30)
best_path, best_distance, distance_history = tsp.run()
print(f"\n最优路径: {best_path}")
print(f"最短距离: {best_distance:.2f}")
tsp.plot_solution()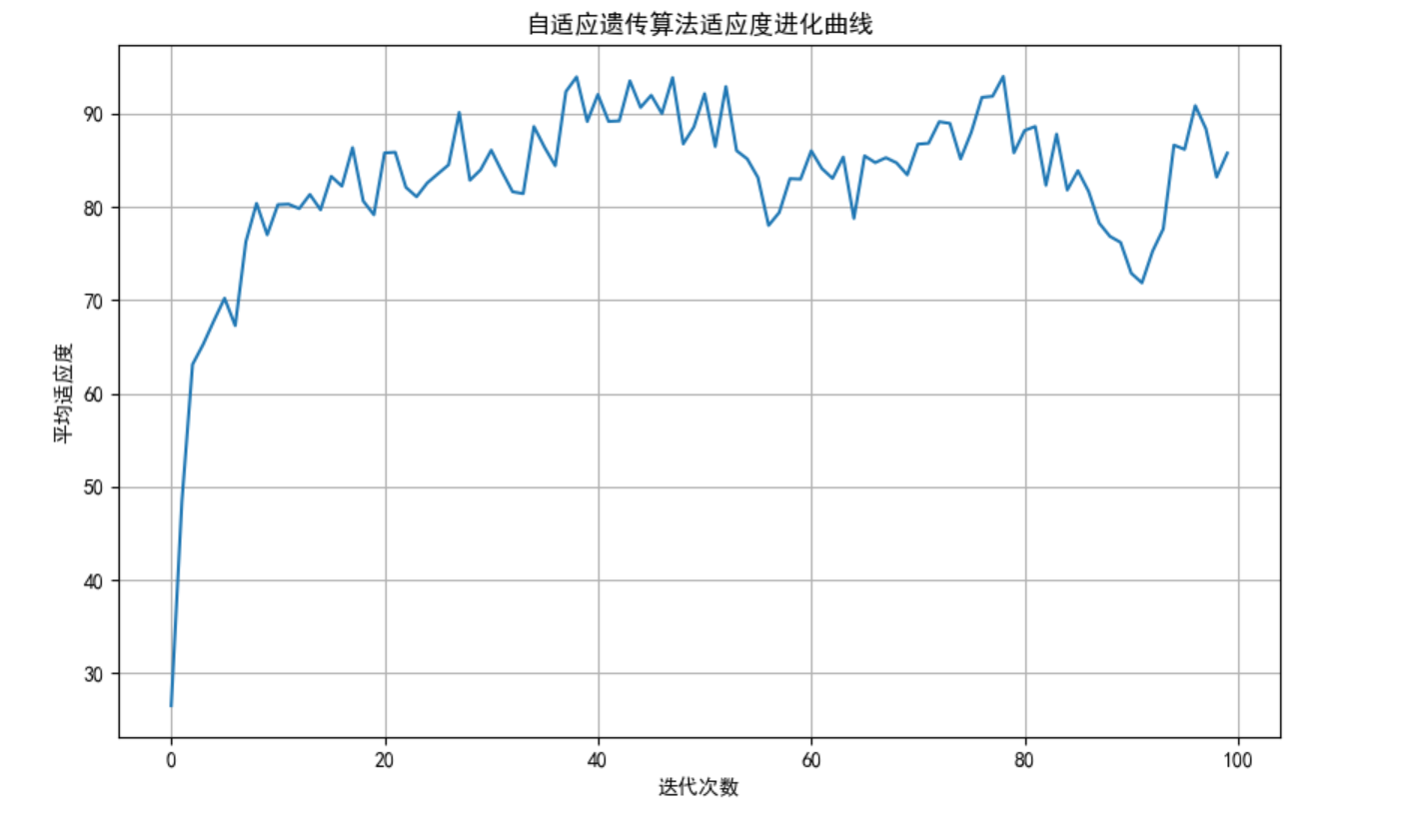
6.5 群智能算法产生的背景
群智能算法 (Swarm Intelligence) 起源于对自然界生物群体行为的研究,如鸟群、鱼群、蚁群等。这类算法的特点是:
- 无集中控制机制:个体通过局部交互实现群体智能
- 自组织性:群体行为通过简单规则涌现
- 鲁棒性:个别个体故障不影响整体性能
- 灵活性:对环境变化有自适应能力
常见的群智能算法包括粒子群优化算法、蚁群算法、人工蜂群算法等。
6.6 粒子群优化算法及其应用
6.6.1 粒子群优化算法的基本原理
粒子群优化算法 (Particle Swarm Optimization, PSO) 由 Kennedy 和 Eberhart 于 1995 年提出,模拟鸟群觅食行为。每个粒子代表一个潜在解,通过以下公式更新位置和速度:

6.6.2 粒子群优化算法的参数分析
- 惯性权重w:控制粒子保持原有速度的趋势,较大的w适合全局探索,较小的适合局部开发
- 学习因子(c_1, c_2):控制粒子向个体最优和全局最优学习的强度
- 粒子数量:通常取 20-100,取决于问题复杂度
- 速度限制:避免粒子飞出搜索空间
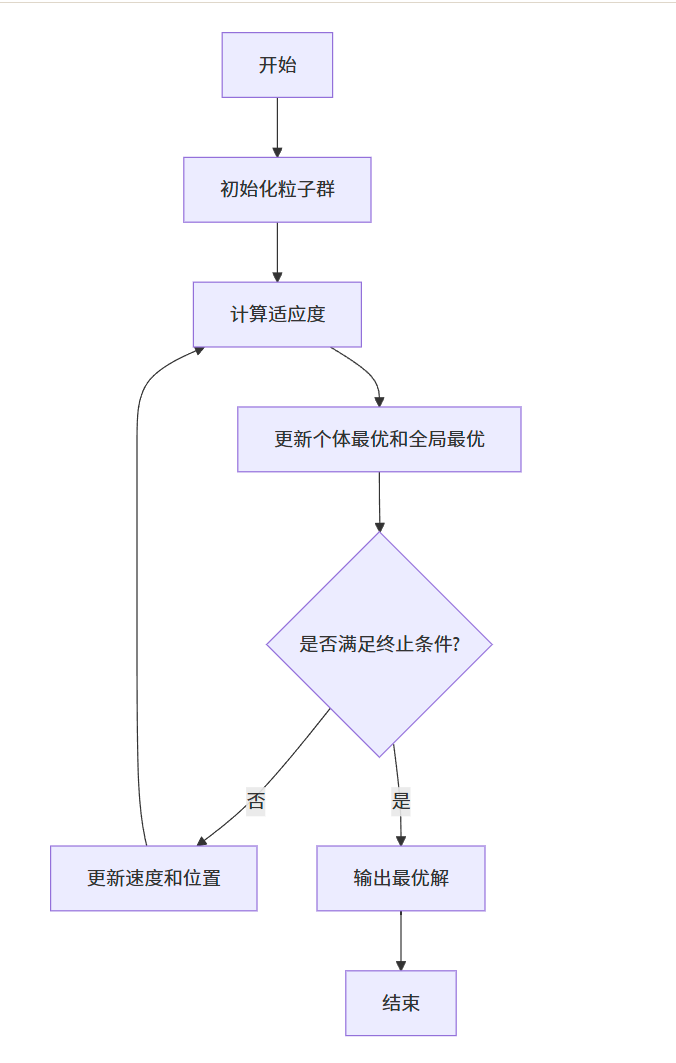
粒子群优化算法流程图
6.6.3 粒子群优化算法求解函数优化问题
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from typing import Callable, Tuple, List
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class ParticleSwarmOptimization:
def __init__(
self,
objective_function: Callable,
dim: int = 2,
population_size: int = 50,
max_iterations: int = 100,
x_range: Tuple[float, float] = (-10, 10),
w: float = 0.7,
c1: float = 1.5,
c2: float = 1.5
):
"""
粒子群优化算法
参数:
objective_function: 目标函数(需最小化)
dim: 问题维度
population_size: 粒子数量
max_iterations: 最大迭代次数
x_range: 变量取值范围
w: 惯性权重
c1, c2: 学习因子
"""
self.objective_function = objective_function
self.dim = dim
self.population_size = population_size
self.max_iterations = max_iterations
self.x_range = x_range
self.w = w
self.c1 = c1
self.c2 = c2
# 初始化粒子位置和速度
self.positions = np.random.uniform(x_range[0], x_range[1], (population_size, dim))
self.velocities = np.random.uniform(-1, 1, (population_size, dim))
# 个体最优位置和适应度
self.pbest_positions = self.positions.copy()
self.pbest_fitness = np.array([objective_function(pos) for pos in self.positions])
# 全局最优位置和适应度
global_best_idx = np.argmin(self.pbest_fitness)
self.gbest_position = self.pbest_positions[global_best_idx].copy()
self.gbest_fitness = self.pbest_fitness[global_best_idx]
self.fitness_history = []
def update_velocities_and_positions(self):
"""更新粒子速度和位置"""
r1, r2 = np.random.random(), np.random.random()
for i in range(self.population_size):
# 速度更新
self.velocities[i] = (
self.w * self.velocities[i] +
self.c1 * r1 * (self.pbest_positions[i] - self.positions[i]) +
self.c2 * r2 * (self.gbest_position - self.positions[i])
)
# 位置更新
self.positions[i] += self.velocities[i]
# 边界处理
self.positions[i] = np.clip(self.positions[i], self.x_range[0], self.x_range[1])
# 计算新位置的适应度
fitness = self.objective_function(self.positions[i])
# 更新个体最优
if fitness < self.pbest_fitness[i]:
self.pbest_fitness[i] = fitness
self.pbest_positions[i] = self.positions[i].copy()
# 更新全局最优
if fitness < self.gbest_fitness:
self.gbest_fitness = fitness
self.gbest_position = self.positions[i].copy()
def run(self) -> Tuple[np.ndarray, float, List[float]]:
"""运行PSO算法"""
for iteration in range(self.max_iterations):
self.update_velocities_and_positions()
# 记录平均适应度
avg_fitness = np.mean(self.pbest_fitness)
self.fitness_history.append(avg_fitness)
if iteration % 10 == 0:
print(f"Iteration {iteration}, Best fitness: {self.gbest_fitness:.6f}, Avg fitness: {avg_fitness:.6f}")
return self.gbest_position, self.gbest_fitness, self.fitness_history
# 测试函数: Sphere函数 f(x) = sum(xi^2)
def sphere_function(x):
return np.sum(x ** 2)
# 运行PSO算法
if __name__ == "__main__":
# 2维Sphere函数优化
pso = ParticleSwarmOptimization(
objective_function=sphere_function,
dim=2,
population_size=50,
max_iterations=100,
x_range=(-10, 10)
)
best_position, best_fitness, fitness_history = pso.run()
print(f"\n最优解: x = {best_position}, f(x) = {best_fitness}")
# 绘制适应度变化曲线
plt.figure(figsize=(10, 6))
plt.plot(fitness_history)
plt.title('平均适应度随迭代次数的变化')
plt.xlabel('迭代次数')
plt.ylabel('平均适应度')
plt.grid(True)
plt.show()
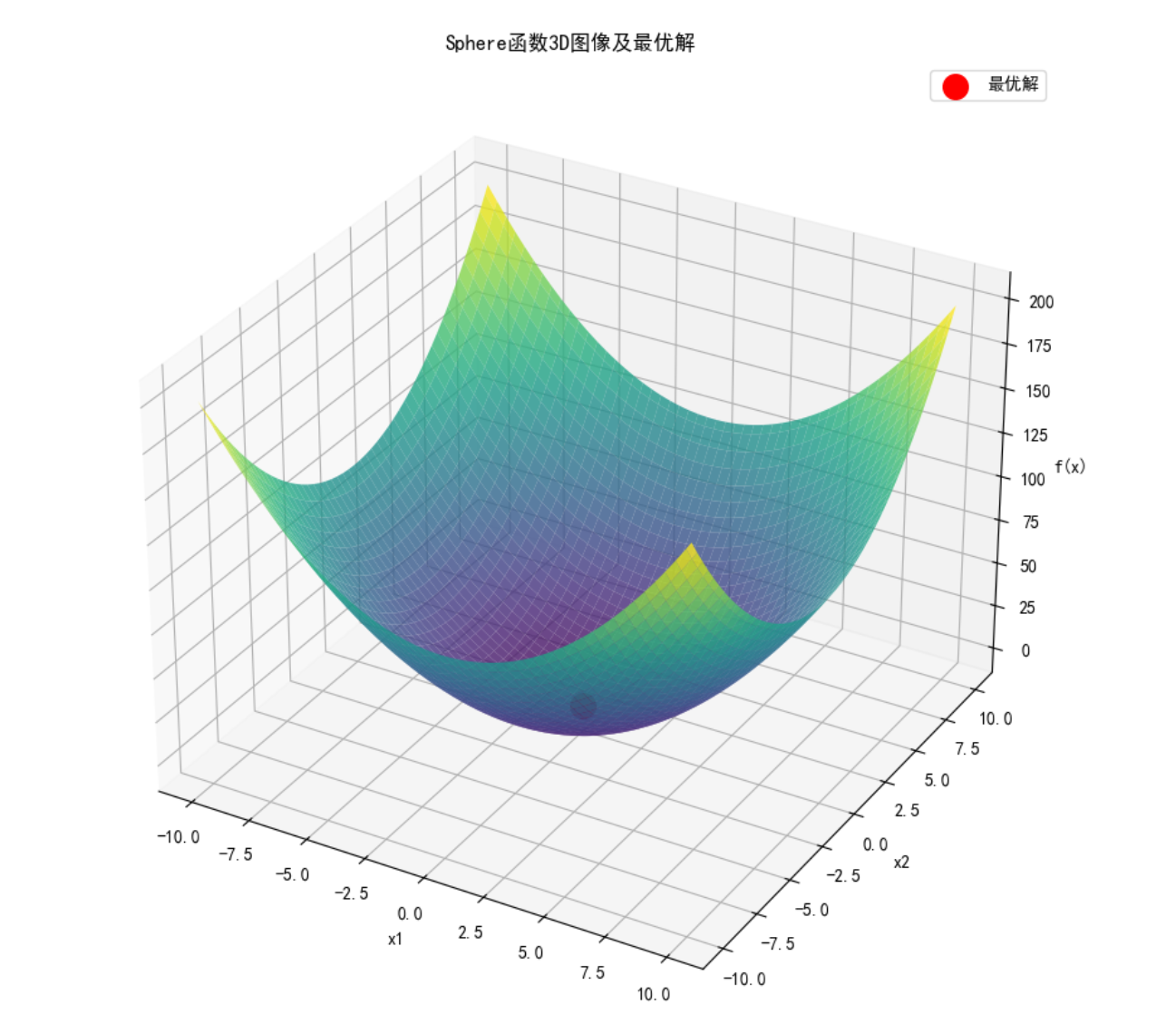
# 绘制3D函数图像和最优解(仅2维问题)
if pso.dim == 2:
x = np.linspace(pso.x_range[0], pso.x_range[1], 100)
y = np.linspace(pso.x_range[0], pso.x_range[1], 100)
X, Y = np.meshgrid(x, y)
# 修正Z的计算方式,确保是2维数组
Z = np.zeros_like(X)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Z[i, j] = sphere_function(np.array([X[i, j], Y[i, j]]))
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax.scatter(best_position[0], best_position[1], best_fitness, color='red', s=200, label='最优解')
ax.set_title('Sphere函数3D图像及最优解')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x)')
ax.legend()
plt.show()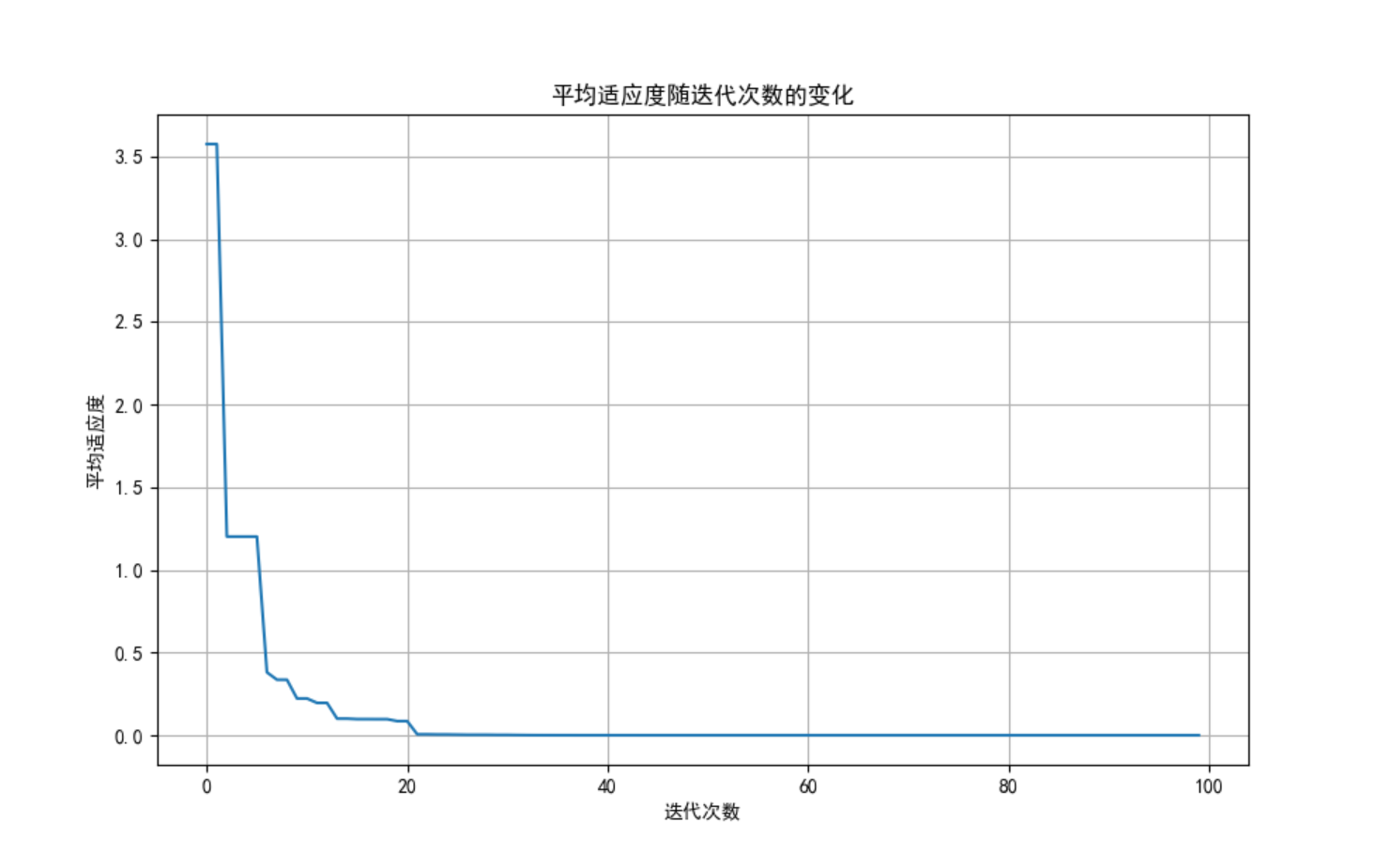
6.6.4 粒子群优化算法求解车辆路径问题
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
from typing import Tuple, List
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class PSOforTSP:
def __init__(
self,
city_num: int = 20,
vehicle_num: int = 5,
population_size: int = 100,
max_iterations: int = 200,
w: float = 0.7,
c1: float = 1.5,
c2: float = 1.5
):
"""
粒子群优化算法求解TSP问题
参数:
city_num: 城市数量
vehicle_num: 车辆数量
population_size: 粒子数量
max_iterations: 最大迭代次数
w, c1, c2: PSO参数
"""
self.city_num = city_num
self.vehicle_num = vehicle_num
self.population_size = population_size
self.max_iterations = max_iterations
self.w = w
self.c1 = c1
self.c2 = c2
# 随机生成城市坐标
self.cities = np.random.rand(city_num, 2) * 100
# depot位置(第一个城市)
self.depot = self.cities[0]
# 初始化粒子(路径表示)
self.positions = self._initialize_positions()
# 初始化速度(与路径长度一致)
self.velocities = np.random.random((population_size, self.city_num - 1))
# 个体最优和全局最优
self.pbest_positions = self.positions.copy()
self.pbest_fitness = np.array([self._calculate_fitness(path) for path in self.positions])
global_best_idx = np.argmin(self.pbest_fitness)
self.gbest_position = self.pbest_positions[global_best_idx].copy()
self.gbest_fitness = self.pbest_fitness[global_best_idx]
self.fitness_history = []
def _initialize_positions(self) -> np.ndarray:
"""初始化粒子位置(路径)"""
positions = np.zeros((self.population_size, self.city_num - 1), dtype=int)
for i in range(self.population_size):
# 随机生成路径(不包括depot,城市索引从1开始)
path = np.random.permutation(self.city_num - 1) + 1
positions[i] = path
return positions
def _calculate_distance(self, path: np.ndarray) -> float:
"""计算路径总距离"""
distance = 0
vehicle_paths = self._split_path(path)
for vehicle_path in vehicle_paths:
if len(vehicle_path) == 0:
continue
# 从depot出发
current = self.depot
for city_idx in vehicle_path:
distance += np.sqrt(np.sum((self.cities[city_idx] - current) ** 2))
current = self.cities[city_idx]
# 返回depot
distance += np.sqrt(np.sum((self.depot - current) ** 2))
return distance
def _split_path(self, path: np.ndarray) -> List[np.ndarray]:
"""将路径分配给多辆车"""
vehicle_paths = [np.array([], dtype=int) for _ in range(self.vehicle_num)]
for i, city_idx in enumerate(path):
vehicle_idx = i % self.vehicle_num
vehicle_paths[vehicle_idx] = np.append(vehicle_paths[vehicle_idx], city_idx)
return vehicle_paths
def _calculate_fitness(self, path: np.ndarray) -> float:
"""计算适应度(距离+惩罚项)"""
distance = self._calculate_distance(path)
vehicle_paths = self._split_path(path)
max_load = max([len(p) for p in vehicle_paths])
balance_penalty = 10 * (max_load - (len(path) / self.vehicle_num)) ** 2
return distance + balance_penalty
def _velocity_to_permutation(self, velocity: np.ndarray, current_path: np.ndarray) -> np.ndarray:
"""将速度映射为排列(路径)"""
priority = velocity.copy()
# 保留当前路径的相对顺序作为启发
for i, city in enumerate(current_path):
priority[city - 1] += 0.5 # 给当前路径中的城市更高优先级
# 排序生成新路径
new_path = np.argsort(priority) + 1 # 转换为城市索引(1-based)
return new_path[:self.city_num - 1] # 确保路径长度正确
def _path_to_priority(self, path: np.ndarray) -> np.ndarray:
"""将路径转换为优先级向量(长度为city_num)"""
priority = np.zeros(self.city_num)
for i, city in enumerate(path):
priority[city - 1] = i + 1
return priority
def update_velocities_and_positions(self):
"""更新粒子速度和位置(修正了形状匹配问题)"""
r1, r2 = np.random.random(), np.random.random()
for i in range(self.population_size):
# 计算优先级向量(长度为city_num)
pbest_priority = self._path_to_priority(self.pbest_positions[i])
current_priority = self._path_to_priority(self.positions[i])
gbest_priority = self._path_to_priority(self.gbest_position)
# 速度更新(现在操作数形状一致)
self.velocities[i] = (
self.w * self.velocities[i] +
self.c1 * r1 * (pbest_priority[self.positions[i] - 1] - current_priority[self.positions[i] - 1]) +
self.c2 * r2 * (gbest_priority[self.positions[i] - 1] - current_priority[self.positions[i] - 1])
)
# 位置更新
new_path = self._velocity_to_permutation(self.velocities[i], self.positions[i])
self.positions[i] = new_path
# 计算适应度
fitness = self._calculate_fitness(new_path)
# 更新个体最优和全局最优
if fitness < self.pbest_fitness[i]:
self.pbest_fitness[i] = fitness
self.pbest_positions[i] = new_path.copy()
if fitness < self.gbest_fitness:
self.gbest_fitness = fitness
self.gbest_position = new_path.copy()
def run(self) -> Tuple[np.ndarray, float, List[float]]:
"""运行PSO算法"""
for iteration in range(self.max_iterations):
self.update_velocities_and_positions()
avg_fitness = np.mean(self.pbest_fitness)
self.fitness_history.append(avg_fitness)
if iteration % 10 == 0:
print(f"Iteration {iteration}, Best fitness: {self.gbest_fitness:.2f}, Avg fitness: {avg_fitness:.2f}")
return self.gbest_position, self.gbest_fitness, self.fitness_history
def plot_solution(self):
"""绘制最优解"""
if self.gbest_position is None:
print("请先运行算法获取最优路径")
return
plt.figure(figsize=(12, 10))
# 绘制城市
plt.scatter(self.cities[:, 0], self.cities[:, 1], c='blue', s=100)
plt.scatter(self.depot[0], self.depot[1], c='red', s=200, marker='*', label=' depot')
for i, city in enumerate(self.cities):
plt.text(city[0] + 1, city[1] + 1, f'城市{i}', fontsize=10)
# 绘制车辆路径
vehicle_paths = self._split_path(self.gbest_position)
colors = ['r', 'g', 'b', 'c', 'm', 'y', 'k']
for i, path in enumerate(vehicle_paths):
if len(path) == 0:
continue
color = colors[i % len(colors)]
# 从depot出发
x = [self.depot[0], self.cities[path[0], 0]]
y = [self.depot[1], self.cities[path[0], 1]]
for j in range(1, len(path)):
x.append(self.cities[path[j], 0])
y.append(self.cities[path[j], 1])
# 返回depot
x.append(self.depot[0])
y.append(self.depot[1])
plt.plot(x, y, color=color, linewidth=2, label=f'车辆{i + 1}')
plt.title(f'多车辆路径优化 (总距离: {self.gbest_fitness:.2f})')
plt.xlabel('X坐标')
plt.ylabel('Y坐标')
plt.legend()
plt.grid(True)
plt.show()
# 绘制适应度变化曲线
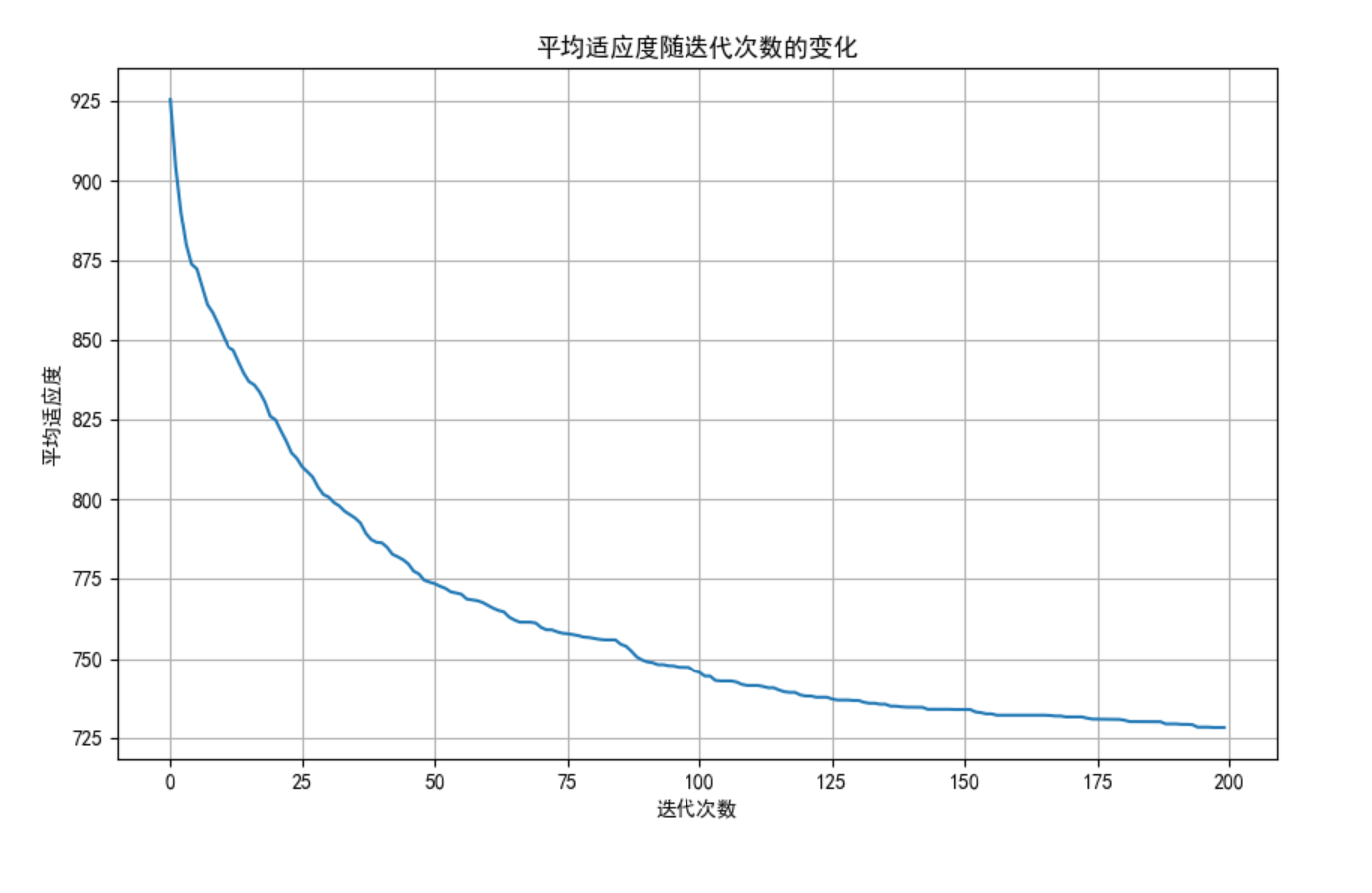
plt.figure(figsize=(10, 6))
plt.plot(self.fitness_history)
plt.title('平均适应度随迭代次数的变化')
plt.xlabel('迭代次数')
plt.ylabel('平均适应度')
plt.grid(True)
plt.show()
# 运行PSO求解TSP
if __name__ == "__main__":
pso_tsp = PSOforTSP(city_num=20, vehicle_num=3)
best_path, best_fitness, fitness_history = pso_tsp.run()
print(f"\n最优路径: {best_path}")
print(f"最小距离: {best_fitness:.2f}")
pso_tsp.plot_solution()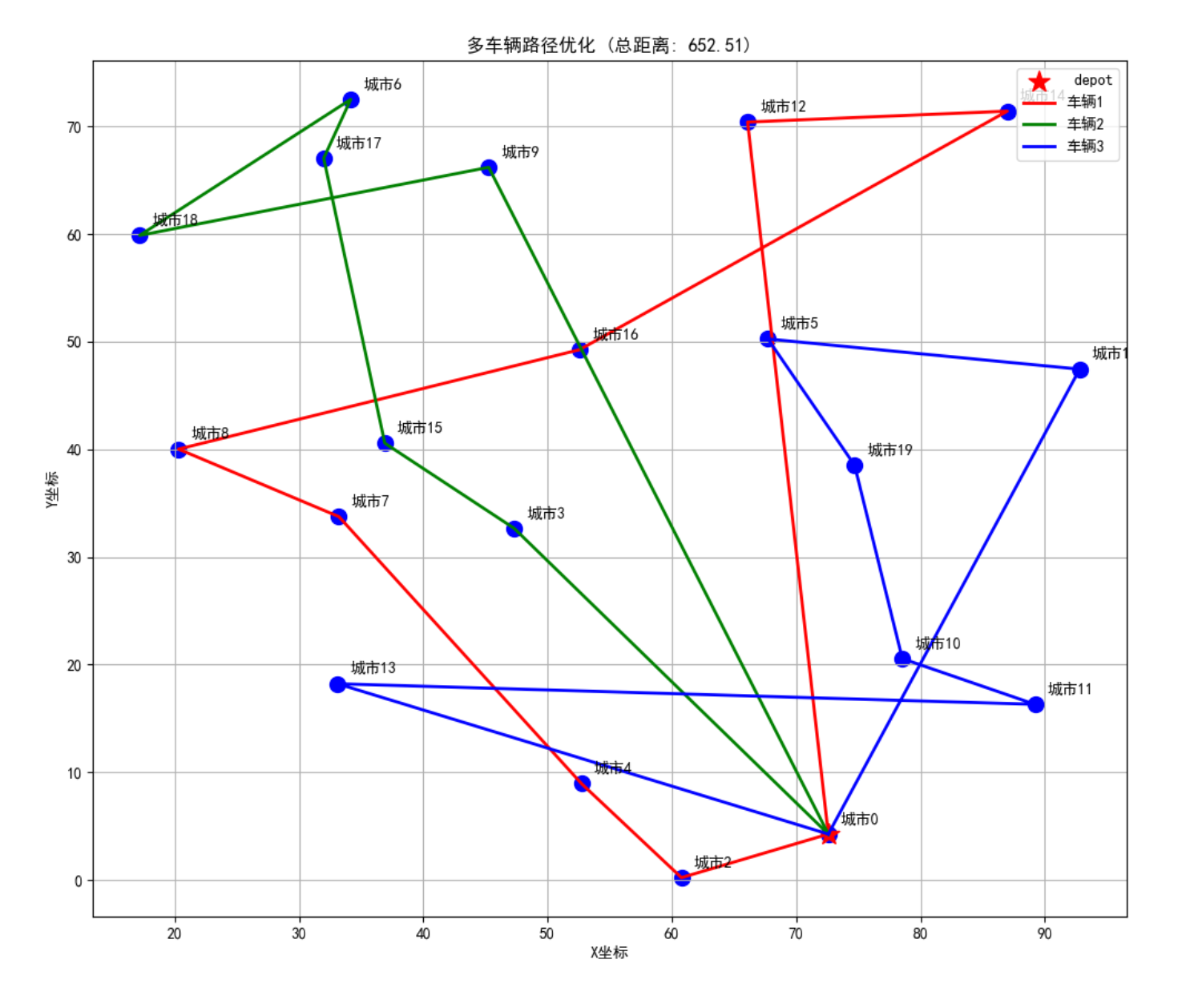
6.7 蚁群算法及其应用
6.7.1 基本蚁群算法模型
蚁群算法 (Ant Colony Optimization, ACO) 模拟蚂蚁觅食过程中分泌信息素的行为,通过信息素的积累和挥发来寻找最优路径。
基本模型包含以下要素:
- 蚂蚁:每个蚂蚁构建一个解
- 信息素:表示路径的优劣程度,随时间挥发
- 状态转移规则:根据信息素和启发式信息选择下一个节点
- 信息素更新:优化解的路径上增加更多信息素
6.7.2 蚁群算法的参数选择
- 蚂蚁数量:通常为城市数量的 1-2 倍
- 信息素重要程度参数 α:控制信息素对选择的影响
- 启发式因子重要程度参数 β:控制启发式信息的影响
- 信息素挥发系数 ρ:通常取 0.1-0.5
- 信息素增强系数 Q:决定每次迭代中信息素的增加量
蚁群算法流程图
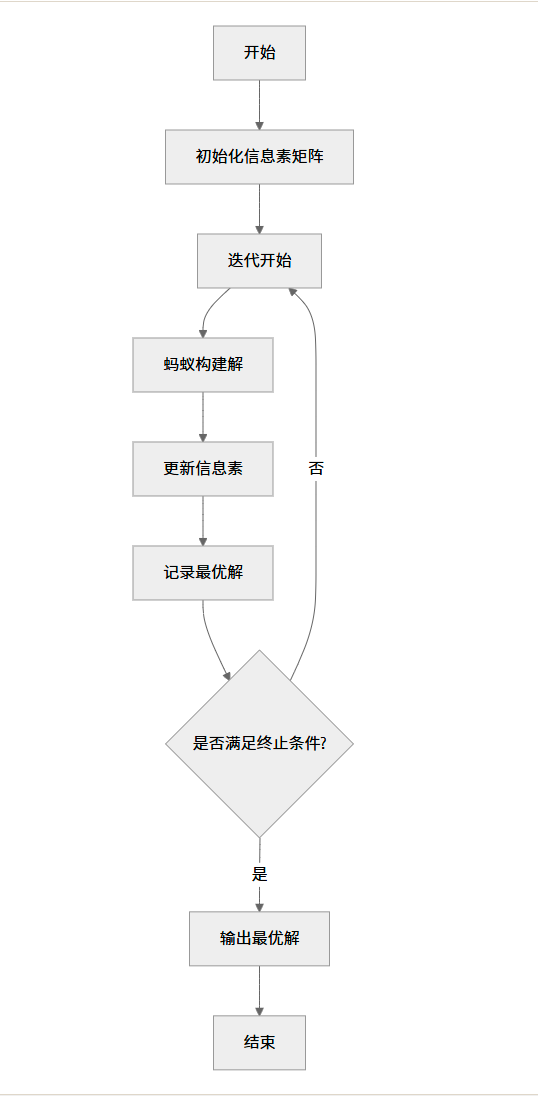
6.7.3 蚁群算法求解 TSP 问题
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
from typing import List, Tuple # 增加List的导入
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class AntColonyOptimization:
def __init__(
self,
city_num: int = 20,
ant_num: int = 30,
max_iterations: int = 100,
alpha: float = 1.0,
beta: float = 2.0,
rho: float = 0.1,
q0: float = 0.9,
q: float = 100
):
"""
蚁群算法求解TSP问题
参数:
city_num: 城市数量
ant_num: 蚂蚁数量
max_iterations: 最大迭代次数
alpha: 信息素重要程度
beta: 启发式因子重要程度
rho: 信息素挥发系数
q0: 贪婪系数
q: 信息素增强系数
"""
self.city_num = city_num
self.ant_num = ant_num
self.max_iterations = max_iterations
self.alpha = alpha
self.beta = beta
self.rho = rho
self.q0 = q0
self.q = q
# 随机生成城市坐标
self.cities = np.random.rand(city_num, 2) * 100
# 计算距离矩阵
self.distance_matrix = cdist(self.cities, self.cities)
# 初始化启发式信息(距离的倒数)
self.heuristic = 1.0 / (self.distance_matrix + 1e-10) # 避免除零
# 初始化信息素矩阵
self.pheromone = np.ones((city_num, city_num))
self.best_path = None
self.best_distance = float('inf')
self.distance_history = []
def select_next_city(self, ant_path: np.ndarray, pheromone: np.ndarray) -> int:
"""选择下一个城市"""
current_city = ant_path[-1]
unvisited = np.setdiff1d(np.arange(self.city_num), ant_path)
if len(unvisited) == 0:
return None # 所有城市已访问
# 计算选择概率
pheromone_values = pheromone[current_city, unvisited] ** self.alpha
heuristic_values = self.heuristic[current_city, unvisited] ** self.beta
selection_probs = pheromone_values * heuristic_values
selection_probs /= np.sum(selection_probs)
# 轮盘赌选择或贪婪选择
if np.random.random() < self.q0:
# 贪婪选择
next_city = unvisited[np.argmax(pheromone_values * heuristic_values)]
else:
# 轮盘赌选择
next_city = np.random.choice(unvisited, p=selection_probs)
return next_city
def construct_solution(self) -> List[np.ndarray]:
"""蚂蚁构建解"""
all_paths = []
for _ in range(self.ant_num):
# 随机选择起点
start_city = np.random.randint(0, self.city_num)
path = np.array([start_city])
while len(path) < self.city_num:
next_city = self.select_next_city(path, self.pheromone)
if next_city is None:
break
path = np.append(path, next_city)
all_paths.append(path)
return all_paths
def update_pheromone(self, paths: List[np.ndarray]):
"""更新信息素"""
# 信息素挥发
self.pheromone *= (1 - self.rho)
# 信息素增强
for path in paths:
distance = self._calculate_distance(path)
# 路径越短,信息素增加越多
pheromone_increase = self.q / distance
for i in range(self.city_num - 1):
city1, city2 = path[i], path[i + 1]
self.pheromone[city1, city2] += pheromone_increase
self.pheromone[city2, city1] += pheromone_increase
# 回到起点
city1, city2 = path[-1], path[0]
self.pheromone[city1, city2] += pheromone_increase
self.pheromone[city2, city1] += pheromone_increase
def _calculate_distance(self, path: np.ndarray) -> float:
"""计算路径距离"""
distance = 0
for i in range(self.city_num - 1):
distance += self.distance_matrix[path[i], path[i + 1]]
# 回到起点
distance += self.distance_matrix[path[-1], path[0]]
return distance
def run(self) -> Tuple[np.ndarray, float, List[float]]:
"""运行蚁群算法"""
for iteration in range(self.max_iterations):
# 蚂蚁构建解
paths = self.construct_solution()
# 计算路径距离
distances = [self._calculate_distance(path) for path in paths]
avg_distance = np.mean(distances)
self.distance_history.append(avg_distance)
# 更新最优解
for path, distance in zip(paths, distances):
if distance < self.best_distance:
self.best_distance = distance
self.best_path = path.copy()
# 更新信息素
self.update_pheromone(paths)
if iteration % 10 == 0:
print(
f"Iteration {iteration}, Best distance: {self.best_distance:.2f}, Avg distance: {avg_distance:.2f}")
return self.best_path, self.best_distance, self.distance_history
def plot_solution(self):
"""绘制最优解"""
if self.best_path is None:
print("请先运行算法获取最优路径")
return
plt.figure(figsize=(10, 8))
# 绘制城市
plt.scatter(self.cities[:, 0], self.cities[:, 1], c='blue', s=100)
for i, city in enumerate(self.cities):
plt.text(city[0] + 1, city[1] + 1, f'城市{i}', fontsize=10)
# 绘制最优路径
path = self.best_path
for i in range(self.city_num - 1):
plt.plot(
[self.cities[path[i], 0], self.cities[path[i + 1], 0]],
[self.cities[path[i], 1], self.cities[path[i + 1], 1]], 'r-')
# 回到起点
plt.plot(
[self.cities[path[-1], 0], self.cities[path[0], 0]],
[self.cities[path[-1], 1], self.cities[path[0], 1]], 'r-')
plt.title(f'旅行商问题最优路径 (距离: {self.best_distance:.2f})')
plt.xlabel('X坐标')
plt.ylabel('Y坐标')
plt.grid(True)
plt.show()
# 绘制距离变化曲线
plt.figure(figsize=(10, 6))
plt.plot(self.distance_history)
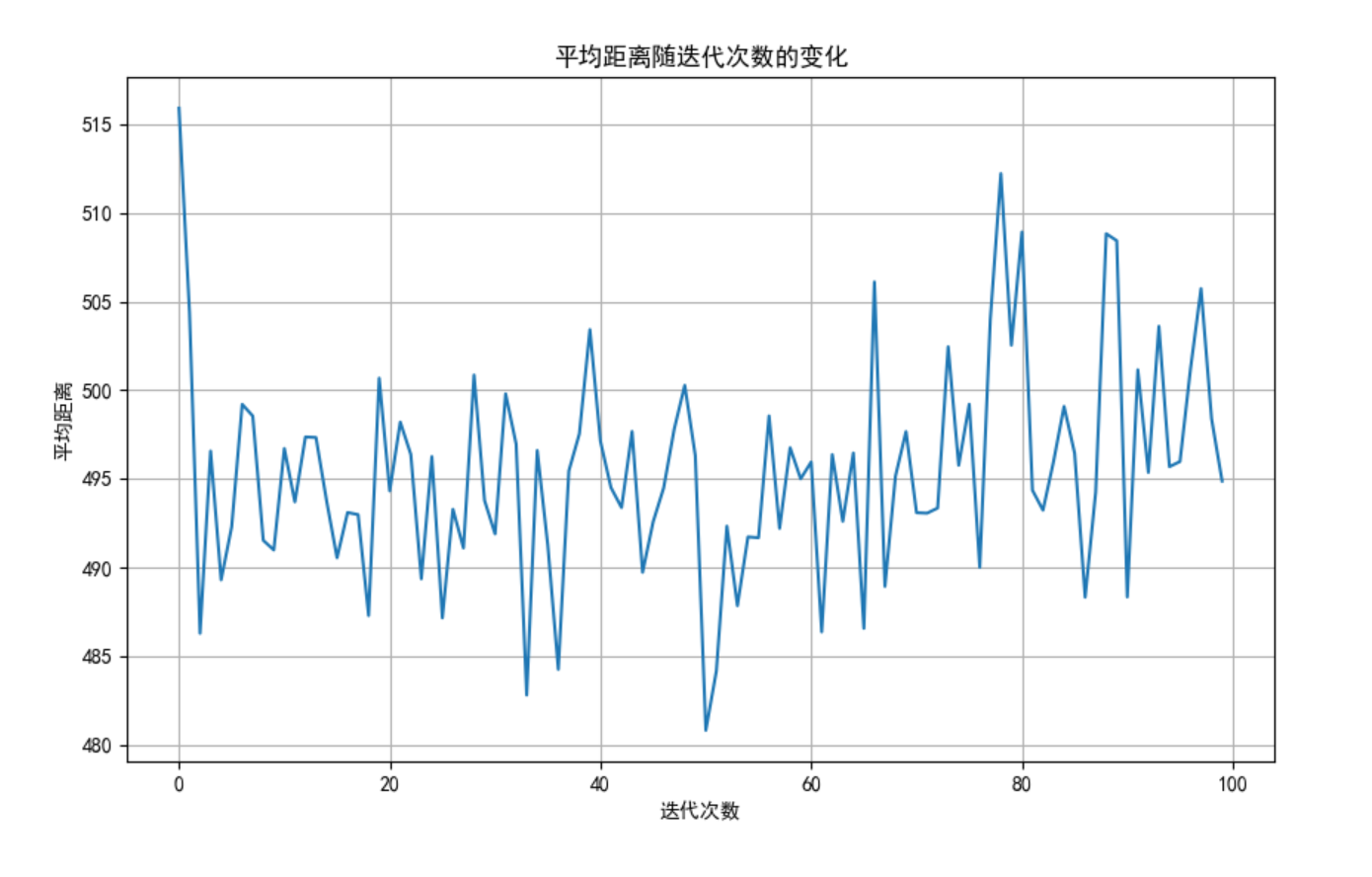
plt.title('平均距离随迭代次数的变化')
plt.xlabel('迭代次数')
plt.ylabel('平均距离')
plt.grid(True)
plt.show()
# 运行蚁群算法
if __name__ == "__main__":
aco = AntColonyOptimization(city_num=20)
best_path, best_distance, distance_history = aco.run()
print(f"\n最优路径: {best_path}")
print(f"最短距离: {best_distance:.2f}")
aco.plot_solution()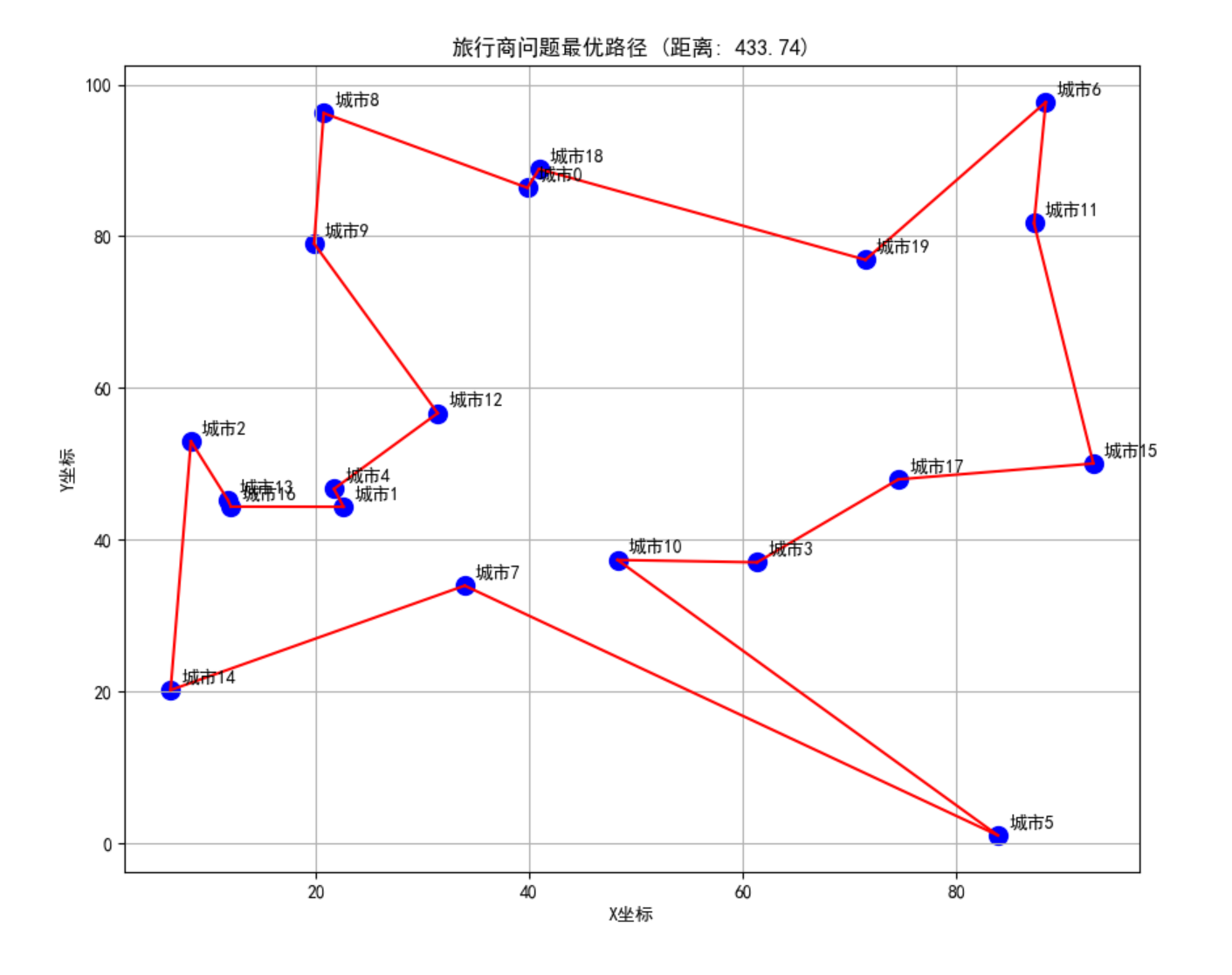
6.8 小结
本章系统介绍了智能计算的核心内容,主要包括:
- 进化算法:从生物学背景出发,阐述了进化算法的基本概念和设计原则。
- 遗传算法:
- 基本遗传算法的各个组成部分,包括编码、选择、交叉、变异等操作
- 三种改进遗传算法:双倍体遗传算法、双种群遗传算法和自适应遗传算法
- 遗传算法在函数优化和旅行商问题中的应用
- 群智能算法:
- 粒子群优化算法的基本原理、参数分析及在函数优化和车辆路径问题中的应用
- 蚁群算法的基本模型、参数选择及 TSP 问题求解
智能计算算法具有自组织、自适应、鲁棒性强等特点,在组合优化、机器学习、工程设计等领域有广泛应用。读者可通过本章的代码实现,进一步理解算法原理并应用于实际问题求解。
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2026-01-20,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

