时频图:同时看时间和频率的分布地图
我们除了时域和频域外还有很多的高级分析,但是常见的不多,近年这个振动啊,轴承啊监测很多,他们不是单纯的电压信号,而是转换成音频,那这样的优点就是可以使用可视化的图片来进行分析,也可以喂给 AI 来做识别。
在这个里面,时域图的信息不好分析,会换到频域,如果时间长了就换成了时频图,其实就是“同时看时间和频率”的地图。
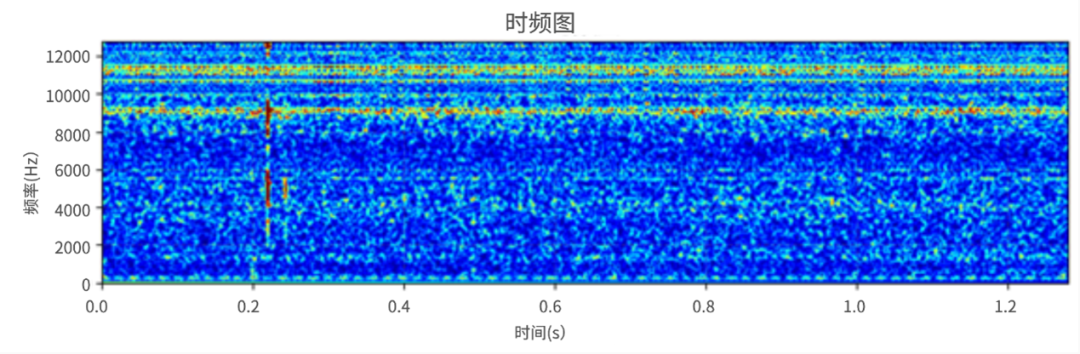
NG电机样品的时频图
NG电机样品的时频图
普通频谱在看什么?
做一次 FFT,得到的是:这整段信号里,包含哪些频率、各自有多强
但它不告诉你这些频率在什么时候出现、是一直在,还是只在某一小段时间冒出来。
比如:1 秒钟的信号,前 0.5 s 是 100 Hz,后 0.5 s 是 500 Hz,做一整段 FFT,你只会看到有 100 Hz 和 500 Hz 两个峰,看不出是先 100Hz 再 500Hz。
时频图在看什么?
时频图就是为了解决这个问题:
频率随时间是怎么变化的?
它把信号切成一小段一小段(时间窗),每一小段都做一次频谱分析(比如 STFT / 小波),然后把结果拼成一个 2D 图:
横轴:时间
纵轴:频率
颜色 / 亮度:在这个时间点、这个频率上,能量/幅度有多大
所以在时频图上能看到:某个频率成分是一直存在的(纵向一条长带),某个频率是某个时刻才突然出现(时间上局部的一块),频率逐渐升高或降低(斜着爬升的轨迹)——比如啸叫、扫频信号、齿轮故障啸叫等。
这类图常见名字有:
Spectrogram(谱图 / 频谱图)——实际上就是一种时频图
波形 → 短时傅里叶变换(STFT)→ → 时频图
背后的“滑动 FFT”(以 STFT 为例)
典型做法(短时傅里叶变换 STFT):
- 取一个时间窗函数 (比如 Hann 窗)
- 把信号在时间 附近“截一小段”:
- 对这小段做 FFT,得到这一时刻 的频谱
- 然后让 一点点往前滑,就得到一堆不同时间的频谱
数学形式(只做个认识就好):
把 或 画成彩色图,就是时频图。
时频图的“本质矛盾”:时间分辨率 vs 频率分辨率
因为要用“时间窗”来截取一小段信号:
窗 越短:
时间定位越准(能看清“短瞬间发生了什么”)但频率分辨率变差(频谱变粗糙、带宽变宽)
窗 越长:
频率分辨率越好(峰更尖锐),但时间定位变差(信号在这长窗内何时发生不清楚)
这就是常说的时频分辨率折中。
用时频图能回答的问题
时频图特别适合回答这类问题:
这个机械振动 / 音频信号里:什么时候开始出现高频成分?某个故障特征频率是一直在,还是偶尔冒出来?
雷达 / 通信信号:频率是如何扫频的?(chirp)哪个时间段有干扰、哪段频率被占用?
生物信号(脑电 EEG、心音、语音):某种节律活动在什么时间段增强 / 减弱?说话时元音 / 辅音,能看到形式频率轨迹
一句话总结:
FFT 告诉你“这段时间里有什么频率”,时频图告诉你“这些频率是什么时候出现的、怎么变化的”。
仿真
:
信号:前 0.5 s 是 100 Hz 正弦,后 0.5 s 是 300 Hz 正弦 采样率:fs = 2000 Hz,总时长 1 s
3 张图:
时域波形:看时间上长什么样
整段 FFT 频谱:只看整体有哪些频率
时频图(STFT 谱图):看频率随时间怎么变
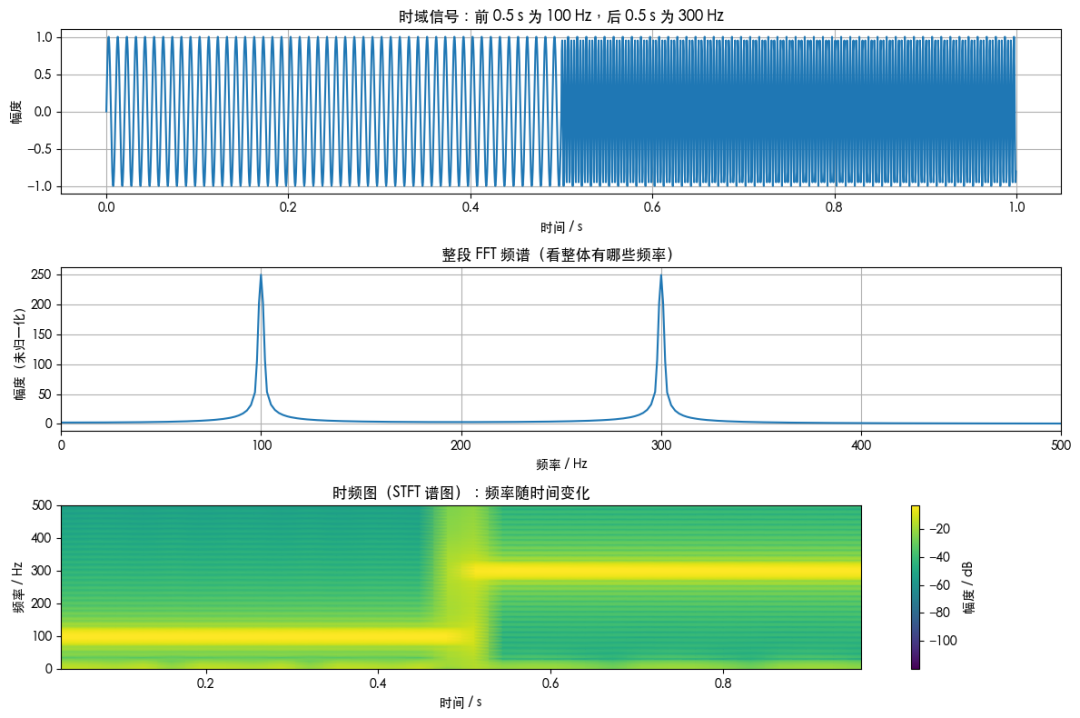
时域波形
前 0.5 s:比较长的周期(100 Hz,周期 10 ms)
后 0.5 s:周期变短(300 Hz,周期 ≈ 3.33 ms)
肉眼可以隐约看出“后面抖得更快了”,但不太直观地看出“具体是 100 Hz → 300 Hz”
整段 FFT 频谱
会在频谱上看到:在 100 Hz 附近有一个峰,在 300 Hz 附近还有一个峰
但是注意:
FFT 完全不知道“100 Hz 是前半段出现、300 Hz 是后半段出现”,只知道“这一整段 1 s 里面同时存在这两个频率成分”。
就像把整首歌扔进频谱分析里,只知道歌里有鼓、吉他、小提琴,但不知道它们是在哪一段进来的。
时频图(谱图)
在时频图上,会看到:
时间 0 ~ 0.5 s 左右:在 100 Hz 附近有一条亮带
时间 0.5 ~ 1.0 s 左右:在 300 Hz 附近有一条亮带
中间会有一点过渡模糊,这是因为 STFT 的时间窗有长度,不可能“刚好在 0.5 s”瞬间断开(时频分辨率折中)
这张图就把“频率随时间怎么变”非常直观地画出来了。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import spectrogram, get_window
# ================================
# 1. 生成信号:前半段 100 Hz,后半段 300 Hz
# ================================
fs = 2000 # 采样率 2000 Hz
T = 1.0 # 总时长 1 秒
N = int(fs * T) # 总采样点数
t = np.arange(N) / fs
# 前半段:100 Hz
x1 = np.sin(2 * np.pi * 100 * t[:N//2])
# 后半段:300 Hz
x2 = np.sin(2 * np.pi * 300 * t[N//2:])
# 拼成一整段信号
x = np.concatenate([x1, x2])
# ================================
# 2. 做整段 FFT,看“整体频谱”
# ================================
# 为了更清晰,使用一个简单的窗函数(汉宁窗)
window = np.hanning(N)
X = np.fft.rfft(x * window)
freqs = np.fft.rfftfreq(N, d=1/fs)
X_mag = np.abs(X)
# ================================
# 3. 做 STFT / 谱图(时频图)
# ================================
# 选择一段时间窗长度,比如 64 ms → 0.064 * 2000 ≈ 128 点
nperseg = 128
noverlap = nperseg // 2 # 50% 重叠
win = get_window("hann", nperseg)
f_stft, t_stft, Sxx = spectrogram(
x,
fs=fs,
window=win,
nperseg=nperseg,
noverlap=noverlap,
nfft=512, # 频率点插值多一点,看着更平滑
scaling='spectrum',
mode='magnitude'
)
# ================================
# 4. 画图:时域 + 整体频谱 + 时频图
# ================================
plt.figure(figsize=(12, 8))
# --- (1) 时域波形 ---
plt.subplot(3, 1, 1)
plt.plot(t, x)
plt.title("时域信号:前 0.5 s 为 100 Hz,后 0.5 s 为 300 Hz")
plt.xlabel("时间 / s")
plt.ylabel("幅度")
plt.grid(True)
# --- (2) 整段 FFT 频谱 ---
plt.subplot(3, 1, 2)
plt.plot(freqs, X_mag)
plt.xlim(0, 500) # 只看 0~500 Hz 比较清晰
plt.title("整段 FFT 频谱(看整体有哪些频率)")
plt.xlabel("频率 / Hz")
plt.ylabel("幅度(未归一化)")
plt.grid(True)
# --- (3) 时频图(谱图) ---
plt.subplot(3, 1, 3)
# 这里用 10*log10 做成 dB 标度,看着更直观
Sxx_dB = 10 * np.log10(Sxx + 1e-12) # 防止 log(0)
plt.pcolormesh(t_stft, f_stft, Sxx_dB, shading='gouraud')
plt.colorbar(label="幅度 / dB")
plt.title("时频图(STFT 谱图):频率随时间变化")
plt.xlabel("时间 / s")
plt.ylabel("频率 / Hz")
plt.ylim(0, 500) # 只看 0~500 Hz
plt.tight_layout()
plt.show()本文参与 腾讯云自媒体同步曝光计划,分享自微信公众号。
原始发表:2025-12-14,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录


