青蛙跳台问题和汉诺塔问题（递归的拓展）

一、青蛙跳台问题

1.什么是是青蛙跳台问题？

青蛙跳台是我们常见的一种编程问题

题目：一只青蛙跳上前面的台阶（不可以往回跳），青蛙一次可以跳一级台阶或者两级台阶，现有n级台阶（n自行输入），请问青蛙有多少种跳上最顶端台阶的可能。

2.分析和解决问题

我们如果从正面看这个问题，我们会发现，第一次开始青蛙可以跳一级台阶或者两级台阶，随着次数的增加，要按照顺序计算剩余台阶数，这样太过麻烦。

不妨将问题倒过来看，青蛙的目的是要跳上台阶，那么最后要么是在n-1的位置跳一下，要么是在n-2的位置跳两级台阶于是，这个问题就变成了这个样子

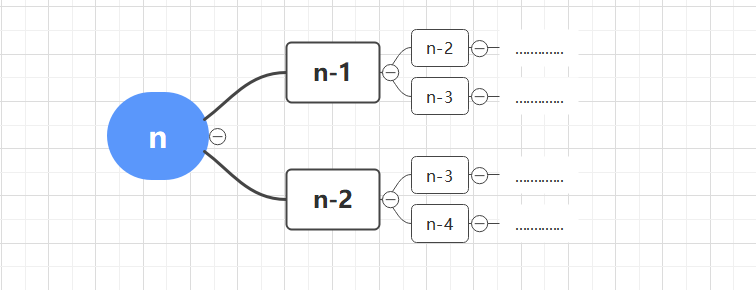
到这里，我们不难看出，这就是斐波那契数列的翻版，于是我们就可以得到这样的程序：

int jump(int n)
{	
	if (n == 1)
		return 1;
	if (n == 2)
		return 2;
	return jump(n - 1) + jump(n - 2);
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int m = jump(n);
	printf("%d\n", m);
	return 0;
}

解析：

输入数据之后，判断，如果不是1或2，就进行return jump(n - 1) + jump(n - 2)，人为让青蛙回到跳上顶点前的位置

接着递归回来接着判断，不都是1或2再次进行递归

如此循环往复，最终青蛙会跳到1或者2的位置上，就可以得到我们想要的结果

（这里的1和2是我们先根据有一级台阶和两级台阶算出来的数据！！！）

二、汉诺塔问题

1.什么是汉诺塔问题

汉诺塔问题是一个经典的递归问题

题目：现有A,B,C三根柱子，在A柱子上从下到上摆放着以大小（越往下，圆盘越大）顺序排列的一摞n个的圆盘（n自行输入），现在需要将A上的圆盘顺序不变的转移到C上，每次只能移动一个圆盘，并且小圆盘要始终在大圆盘的上面，问最快需要多少步才能完成？

2.分析和解决问题

首先，当n=1时，我们可以直接将圆盘移到C上

当n>1时，我们便可以用递归的思想

无论过程怎样，最先要做的一定是把最大的圆盘移动到C上，在这之前的一步，一定是A上仅剩下一个最大的圆盘，B上从下往上、从大到小堆叠着n-1个圆盘（因为规则说了，小圆盘必须在大圆盘上面）。那么这时候B柱也就成为了新的A柱，开始新的操作。

int hanoi(int n)
{
	if (n == 1)
		return 1;
	else
		return 2 * hanoi(n - 1) + 1;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int m=hanoi(n);
	printf("%d\n", m);
	return 0;
}

分析：

如果仅剩下1个圆盘，那么毋庸置疑，它会被移动一次便会结束。

如果剩余的圆盘数量大于一个，我们就进行else操作，直到剩余一个圆盘。

（2 * hanoi(n - 1) + 1）的意思是，现在有n个圆盘（n>1），首先要做的是将上面的n-1个圆盘 移动到辅助柱上（hanoi(n - 1)），然后再去进行下一步，移动最大的圆盘到目标柱上（1），最后还需要再次将辅助柱上的n-1个都放到目标柱上（hanoi(n - 1)），加到一起就有了（2 * hanoi(n - 1) + 1）

3.拓展

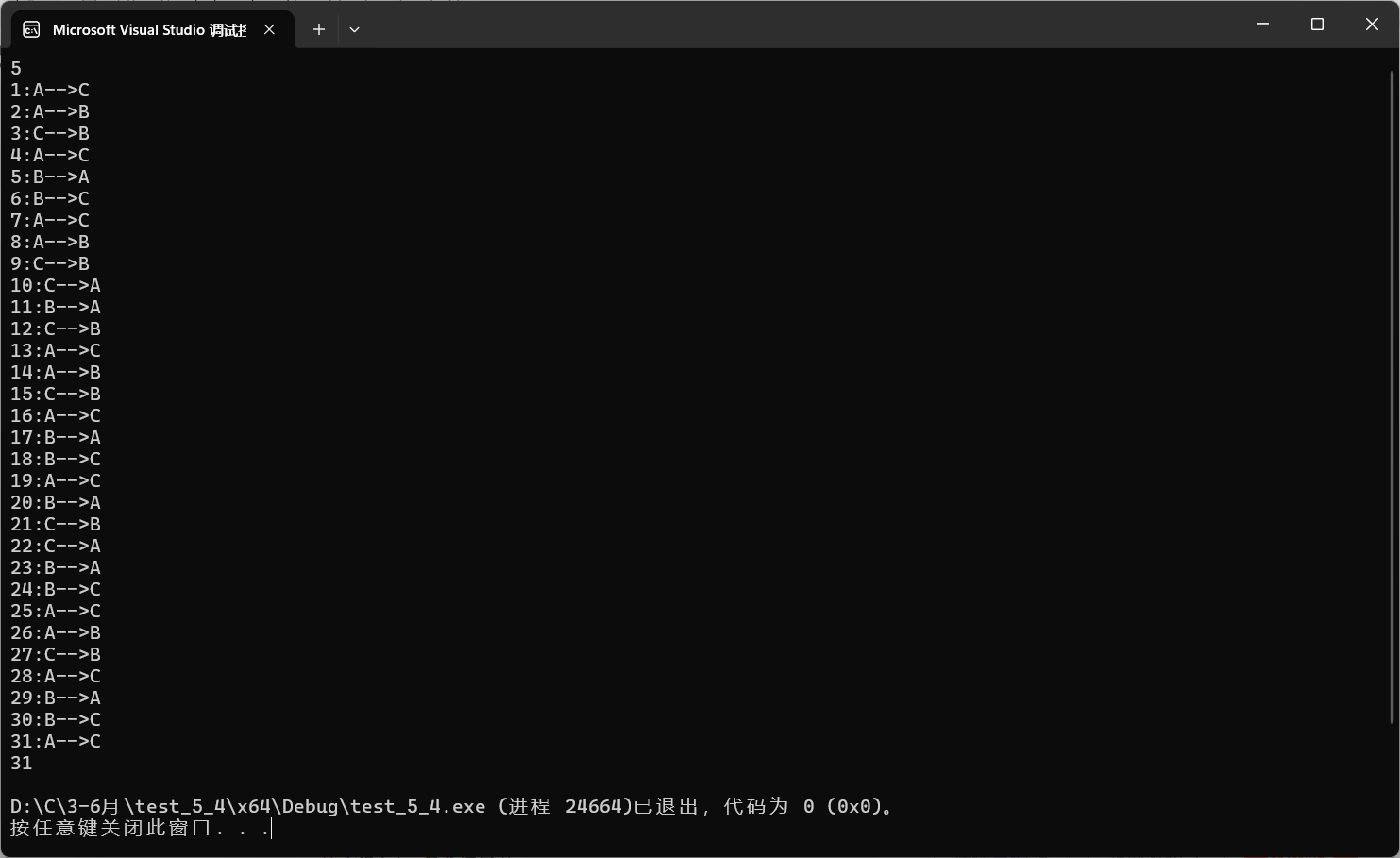
当然，我们还可以对程序进行一点升级，将我们的过程打印出来。

int count = 0;

void hanoi(int n,char from,char aux,char to)
{
	if (n == 1)
	{
		count++;
		printf("%d:%c-->%c\n", count,from, to);
	}
	else
	{
		hanoi(n - 1, from, to, aux);
		count++;
		printf("%d:%c-->%c\n", count, from, to);
		hanoi(n - 1, aux, from, to);
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	hanoi(n,'A','B','C');
	printf("%d\n", count);
	return 0;
}