【操作系统、数学】什么是排队论？如何理解排队论？排队论有什么用处？Queueing Theory？什么是 Little’s Law？

排队论（Queueing Theory）是研究系统中排队现象的数学理论，旨在分析资源分配、服务效率及等待时间等问题。它广泛应用于计算机科学、通信网络、交通规划、工业工程等领域。

【下文会通过搜集的资料，从各方面了解排队论，耐心阅读可能会有所收获：）】

一、排队论的历史背景

• 起源：1909年，丹麦数学家阿格纳·克拉鲁普·厄朗（Agner Krarup Erlang）在研究电话交换系统时首次提出排队论，用于优化电话网络的呼叫阻塞问题。
• 发展：20世纪中期，随着计算机和通信技术的兴起，排队论成为运筹学和系统科学的重要分支，被扩展应用于更复杂的场景。

二、排队系统的核心要素

排队系统的结构可以用“Kendall记号”表示：A/B/C/D/E

【在排队论中，Kendall记号 （Kendall's notation）是一种用于标准化描述排队模型的符号系统，由英国数学家David G. Kendall于1953年提出。】

• A：顾客到达的时间间隔分布（如泊松分布、指数分布）。
• B：服务时间的分布（如指数分布、定长分布）。
• C：服务台（服务器）数量。
• D：系统容量（队列长度上限）。
• E：排队规则（如FCFS先到先服务、优先级服务等）。

1. 顾客到达过程

• 泊松过程（Poisson Process）
  • 假设顾客到达时间间隔服从指数分布，到达率为λ（单位时间到达的顾客数）。【请求到达的时间】
  • 数学特性：无记忆性（即下一个顾客到达的概率与过去无关）。
• 其他分布：定长到达（如周期性到达）、Erlang分布等。

2. 服务过程

• 指数分布服务时间：服务时间服从参数为μ的指数分布，服务率为μ（单位时间服务的顾客数）。【应用的处理能力】
• 一般分布（G）：服务时间可以是任意分布（如正态分布、均匀分布等）。

3. 服务台数量

• 单服务台（如M/M/1模型）：适用于简单系统。
• 多服务台（如M/M/c模型）：多个服务台并行工作，提升系统吞吐量。

4. 系统容量

• 无限队列：假设队列长度无限制（如M/M/1模型）。
• 有限队列：队列满时新到达的顾客被拒绝（如M/M/1/K模型）。

【3和4中提到的各类模型后面会讲，是一些比较经典的排队模型。】

5. 排队规则

• FCFS（先到先服务）：最常见规则。
• 优先级队列：高优先级顾客优先被服务。
• 轮转调度（Round-Robin）：分时服务，常见于操作系统进程调度。

三、经典排队模型与数学分析

以下以M/M/1模型为例，详细说明分析过程：

1. M/M/1模型定义

• 顾客到达为泊松过程（到达率λ）。
• 服务时间服从指数分布（服务率μ）。
• 单服务台，队列容量无限，排队规则为FCFS。

【单服务台，到达为泊松过程（M），服务时间为指数分布（M），无限容量。典型场景：单一窗口的银行柜台。所以这部分的后续理解，可以以银行柜台作为脑海中样例，以便于轻松理解。】

2. 关键性能指标

• 系统利用率（ρ）：服务台的繁忙概率，ρ = λ/μ（要求ρ < 1，否则队列无限增长）。
• 平均队列长度（L_q）：队列中等待的平均顾客数，L_q = ρ² / (1−ρ)。
• 平均系统内顾客数（L）：包括正在服务的顾客，L = λ / (μ−λ)。
• 平均等待时间（W_q）：W_q = L_q / λ = ρ / (μ(1−ρ))。
• 平均逗留时间（W）：包括等待和服务时间，W = W_q + 1/μ。

3. Little定理

【这个比较重要】

描述了系统稳态下的关系：

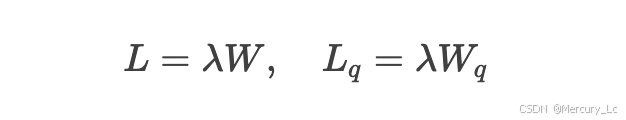
4. 其他经典模型

• M/M/c模型：
  • c个服务台，系统利用率ρ = λ/(cμ)。
  • 平均队列长度公式更复杂，需计算Erlang C公式。
• M/G/1模型：
  • 服务时间为一般分布，需利用Pollaczek-Khinchine公式计算平均队列长度：

  

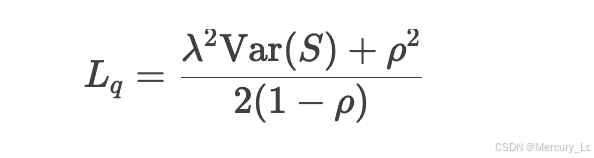
  其中S为服务时间的方差。

• 有限队列模型（如M/M/1/K）：
  • 队列长度上限为K，当队列满时顾客被拒绝。
  • 顾客流失概率：

  

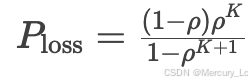
【公式看不懂可以暂时不去推导，后面找时间出文章来给大家分享，现在可以最主要理解排队论是什么，表示什么。】

【这里补充一下对模型的理解：

1. M/M/1
   • 单服务台，到达为泊松过程（M），服务时间为指数分布（M），无限容量。
   • 典型场景：单一窗口的银行柜台。【对这些典型场景有印象就可以】
2. M/M/c
   • 多服务台（c个），到达和服务均为指数分布。
   • 典型场景：多个收银台的超市。
3. M/G/1
   • 单服务台，到达为泊松过程，服务时间服从一般分布（如正态分布）。
   • 典型场景：机器维修（服务时间可能波动较大）。
4. G/G/1/∞/∞/LCFS
   • 一般到达和服务时间分布，单服务台，后到先服务。

】

四、排队论的应用场景

【实际上这部分自己灵活判断吧。我遇到的主要是操作系统中内存的读写问题。】

【其他的例举的场景，也只是从资料和LLM得到的，实践性不知道如何。】

1. 计算机网络

• 数据包调度：优化路由器缓冲区管理，减少网络拥塞。
• 负载均衡：在多服务器系统中分配请求，降低延迟。

2. 操作系统

• 进程调度：通过优先级队列管理CPU时间片分配。
• 磁盘I/O调度：优化读写请求的顺序（如电梯算法）。

3. 云计算与分布式系统

• 任务队列管理：控制虚拟机或容器的任务分配，避免资源过载。
• 微服务架构：通过队列解耦服务，提升系统弹性。

4. 实时系统

• 实时任务处理：保证高优先级任务的低延迟响应。

五、排队论的局限性

1. 假设限制：实际场景可能不符合泊松到达或指数服务时间的假设。【所以说这里需要根据实际情况进行调整】
2. 复杂系统分析困难：多阶段队列、异构服务器等需借助仿真。
3. 动态环境适应：传统模型难以处理时变到达率或动态资源调整。

Little's Law

1. Little 定理的定义

Little 定理描述了排队系统中以下三个关键指标之间的恒等关系：

• 平均队长（L）：系统中顾客的平均数量（包括正在接受服务的顾客）。
• 平均到达率（λ）：单位时间内到达系统的顾客数。
• 平均逗留时间（W）：顾客从进入系统到离开系统的平均时间（包括等待时间和服务时间）。

其数学表达式为：

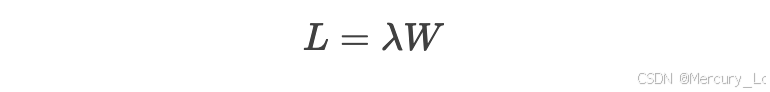
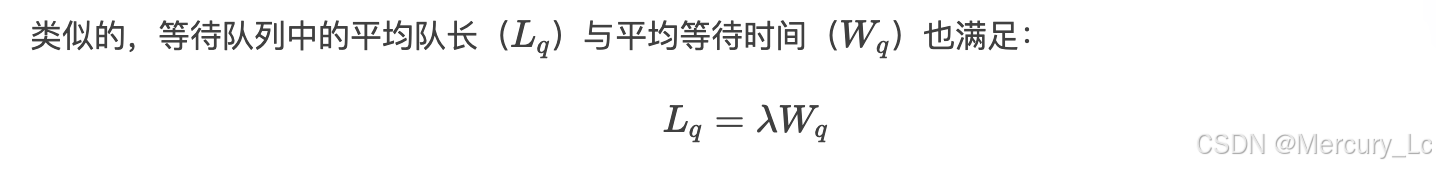
这一关系适用于绝大多数稳态排队系统，无论顾客到达分布、服务时间分布或排队规则如何。

参考与引用：

各大LLMs服务

排队论：服务系统的优化与统计规律-CSDN博客

排队论基础 - 千灵域 - 博客园 (cnblogs.com)

数模培训第三周——排队论 - 蒟蒻颖 - 博客园 (cnblogs.com)

排队论 - pxlsdz - 博客园 (cnblogs.com)