通俗易懂的解释Sparse Convolution过程

来源：信息网络工程研究中心
本文约2400字，建议阅读10分钟 本文作者运用简单的举例和图片对稀疏卷积这一工作进行了详细的阐述。

为什么需要稀疏卷积，稀疏卷积是如何工作的？本文作者运用简单的举例和图片对稀疏卷积这一工作进行了详细的阐述，阅读本文只需“幼儿园智商”即可搞懂稀疏卷积！ 

前言

我之前写过一次稀疏卷积的论文阅读笔记，不过这个才是最易懂的版本（呕心沥血画了好些图）。

阅读本文只需要拥有幼儿园智商即可明白稀疏卷积。

本文的理论部分是在“3D Semantic Segmentation with Submanifold Sparse Convolutional Networks”的基础上完成的。

https://arxiv.org/pdf/1711.10275.pdf

实现部分，是基于“SECOND: Sparsely Embedded Convolutional Detection”的论文。

https://pdfs.semanticscholar.org/5125/a16039cabc6320c908a4764f32596e018ad3.pdf

一、为什么提出稀疏卷积？它有什么好处？（可以跳过这个先看卷积过程）

卷积神经网络已经被证明对于二维图像信号处理是非常有效的。然而，对于三维点云信号，额外的维数 z 显著增加了计算量。

另一方面，与普通图像不同的是，大多数三维点云的体素是空的，这使得三维体素中的点云数据通常是稀疏信号。

稀疏的2D image。其中深灰色像素全为零，浅灰色像素代表非零数据点

稀疏的3D grid

我们是否只能有效地计算稀疏数据的卷积，而不是扫描所有的图像像素或空间体素？

否则这些空白区域带来的计算量太多余了。这就是 sparse convolution 提出的motivation。下面是一个示例，解释了稀疏卷积是如何工作的。

二、举例子之前的定义

为了逐步解释稀疏卷积的概念，使其更易于理解，本文以二维稀疏图像处理为例。由于稀疏信号采用数据列表和索引列表表示，二维和三维稀疏信号没有本质区别。

1. 输入定义

使用以下稀疏图像作为输入：

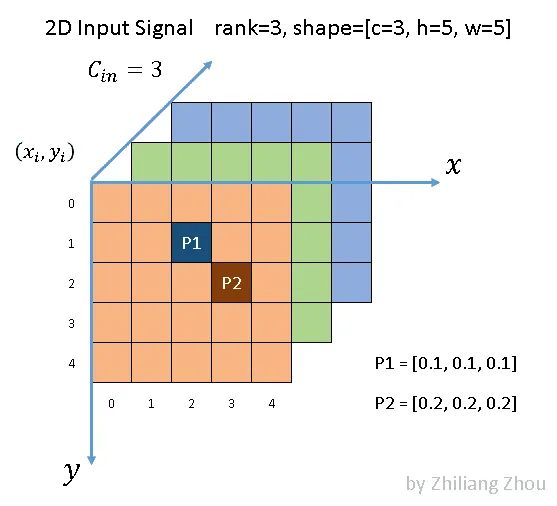
如图所示，我们有一个5 × 5的3通道图像。除了 P1和 P2两点外，所有像素都是(0,0,0) （虽然0这个假设也很不严谨）。根据文献[1] ，P1和 P2，这种非零元素也称为active input sites。

在稀疏格式中，数据列表是[[0.1,0.1,0.1] ，[0.2,0.2,0.2] ，索引列表是[1,2] ，[2,3] ，并且是 YX 顺序。

2. kernel 定义

假设使用以下参数进行卷积操作：

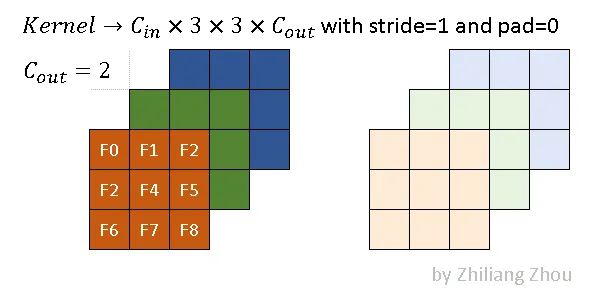
稀疏卷积的卷积核与传统的卷积核相同。上图是一个例子，其内核大小为3x3。

深色和浅色代表两种滤镜。在本例中，我们使用以下卷积参数。

conv2D(kernel_size=3, out_channels=2, stride=1, padding=0)

3. 输出的定义

稀疏卷积的输出与传统的卷积有很大的不同。对于稀疏卷积的发展，有两篇很重要的论文，所以对应的，稀疏卷积也有两种输出。

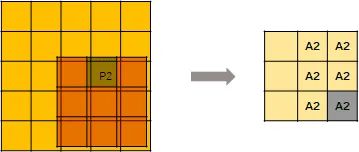
一种是 regular output definition，就像普通的卷积一样，只要kernel 覆盖一个 active input site，就可以计算出output site。

另一个称为submanifold output definition。只有当kernel的中心覆盖一个 active input site时，卷积输出才会被计算。

上图说明了这两种输出之间的区别。

A1代表 active site，即 P1产生的卷积结果。类似地，A2代表从 P2计算出的 active site。A1A2代表 active site，它是 P1和 P2输出的总和。深色和浅色代表不同的输出通道。

好的，假设完了，让我们看看稀疏卷积到底是怎么算的。

三、稀疏卷积的计算过程

1. 构建 Input Hash Table 和 Output Hash Table

现在要把 input 和 Output 都表示成 hash table 的形式。

为什么要这么表示呢？

input hash table和output hash table 对应上图的 Hash_in，和 Hash_out。

对于 Hash_in：v_in 是下标，key_ in 表示value在input matrix中的位置。

现在的input一共两个元素 P1和P2，P1在input matrxi的(2, 1)位置, P2在 input matrix 的(3,2)的位置，并且是 YX 顺序。

是的没错，这里只记录一下p1的位置 ，先不管 p1代表的数字。所以其实可以把这个input hash table命名为 input position hash table。

input hash tabel的构建完成了，接下来构建 output hash table。先来看一下卷积过程中 P1是怎么向下传导的：

用一个kernel去进行卷积操作：

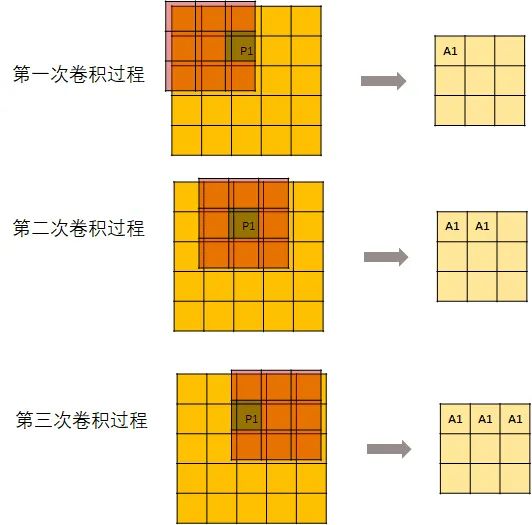
但是，并不是每次卷积kernel都可以刚好碰到P1。所以，从第7次开始，输出的这个矩阵就不再变化了。

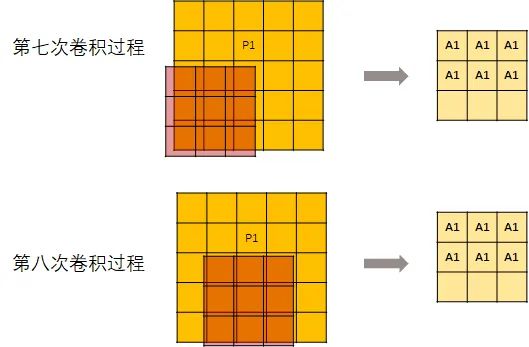
然后记录每个元素的位置。

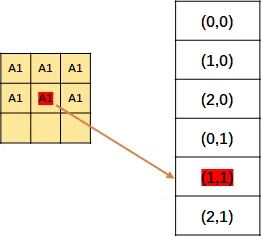
上面说的只是操作P1，当然P2也是同样的操作。

然后把P1, P2的结果结合起来（主要是消除掉重复元素），得到了一张位置表。是的没错，此处记录的还是位置。

然后编号，就得到了 output hash table。

2.构建 Rulebook

第二步是建立规则手册——rulebook。这是稀疏卷积的关键部分！！！（敲黑板了）

规则手册的目的类似于 im2col [5] ，它将卷积从数学形式转化为有效的可编程形式。

但是与 im2col 不同的是，rulebook集合了卷积中所有涉及到的原子运算，然后将它们关联到相应的核元素上。

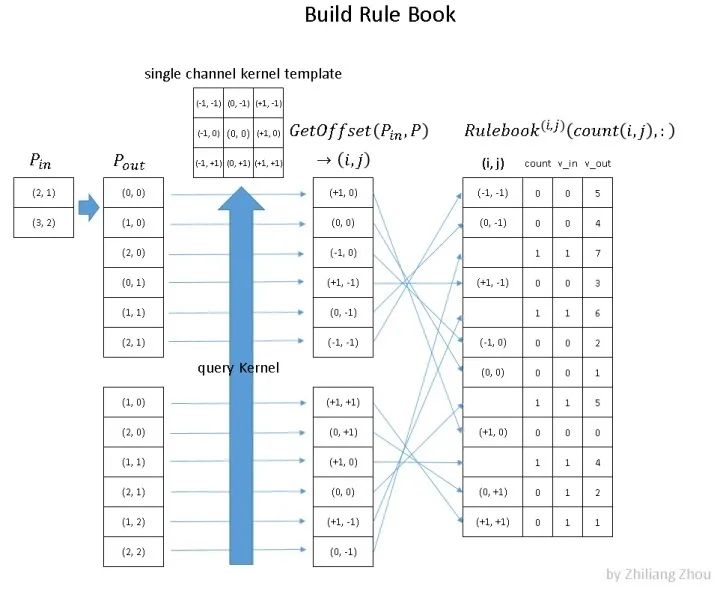
上图就是如何构建 rulebook 的例子。

rulebook的每一行都是一个 atomic operation（这个的定义看下面的列子就知道了），rulebook的第一列是一个索引，第二列是一个计数器count， v_in和 v_ out 分别是atomic operation的 input hash table 的 index和 output hash tabel的index。（没错，到现在为止，依然是index，而没有用到真实的数据。）

atomic operation是什么呢？举个例子。

红色框框表示的是下图的atomic operation。

黄色框框表示的是下图的atomic operation。

因为这个时候(0, -1) 是第二次被遍历到，所以count+1.

3. Computation Pipeline

综上，编程中的过程是什么样子的呢？现在有输入（这个图上面出现过了）。

对它进行卷积操作：

conv2D(kernel_size=3, out_channels=2, stride=1, padding=0)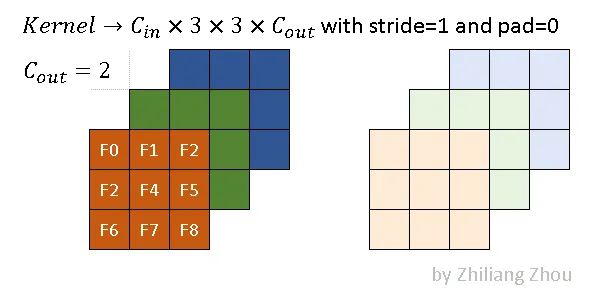

深色和浅色的kernel表示2个不同的kernel，即output channel=2。则，程序里的稀疏卷积过程是：

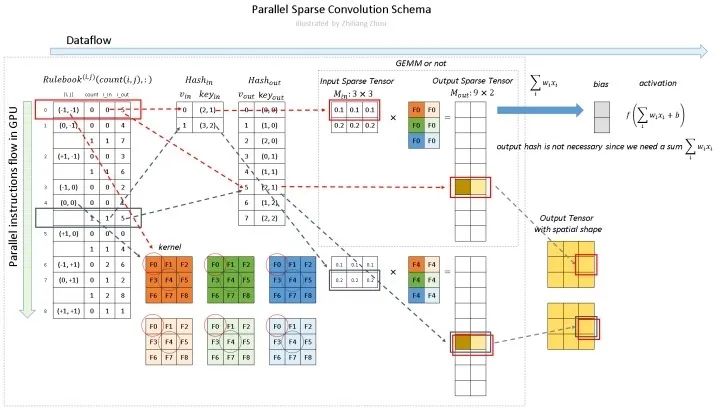
如图所示，稀疏卷积中的卷积计算，不用滑动窗口方法，而是根据rulebook计算所有的原子操作。在图中，红色和蓝色箭头表示两个不同的计算实例。

红色箭头处理rulebook中第一个 atomic operation。从rulebook中，我们知道这个atomic operation 有来自 input index (v_in) =0 位置(2,1)的 P1 的输入，和 output index (v_out) =5 位置 (2,1)的输出。

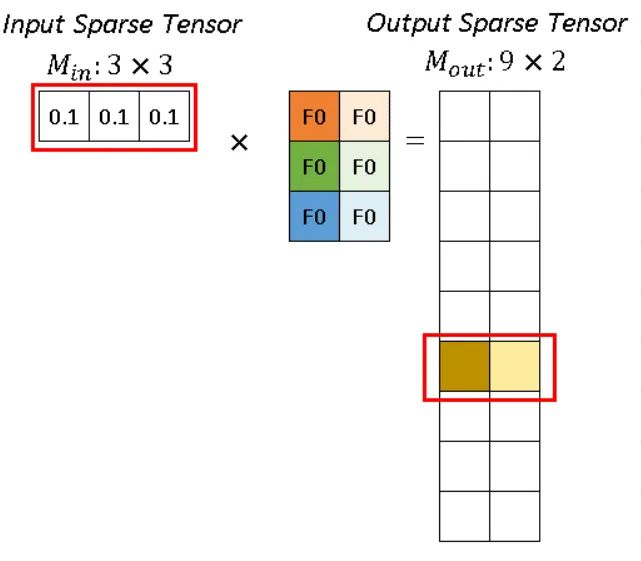
对于p1 代表的 (0.1, 0.1, 0.1)，分别跟深色和浅色两个kernel进行卷积运算，得到深黄色和浅黄色两个channel的输出。

同样，蓝色箭头表示另一个原子操作。

可以看到红色操作和蓝色操作有相同的output index (v_out），没事的，直接把他们的输出加起来就好了。

四、总结

input/output hash tabel只维护那些真正有元素的条目。

所以说，稀疏卷积是非常 efficient的，因为我们只计算非零元素（元素指的是像素 或者 体素）的卷积，而不需要计算所有的元素。

虽然构建 rulebook 也是需要额外的计算开销的，但是这个构建过程也是可以在GPU上并行处理的。

引用：

[1] Graham, Benjamin, Martin Engelcke, and Laurens Van Der Maaten. “3d semantic segmentation with submanifold sparse convolutional networks.”Proceedings of the IEEE conference on computer vision and pattern recognition. 2018.

[2] Yan, Yan, Yuxing Mao, and Bo Li. “Second: Sparsely embedded convolutional detection.”_Sensors_18.10 (2018): 3337.

[3] Li, Xuesong, et al. “Three-dimensional Backbone Network for 3D Object

[4] https://towardsdatascience.com/how-does-sparse-convolution-work-3257a0a8fd1

编辑：黄继彦