《信号与系统》- 第三章 离散系统的时域分析
《信号与系统》- 第三章 离散系统的时域分析

啊阿狸不会拉杆
发布于 2026-01-21 11:50:33
发布于 2026-01-21 11:50:33
3.1 LTI 离散系统的响应
一、差分与差分方程
在离散系统中,差分运算用于描述信号的变化率,常见的有前向差分和后向差分:
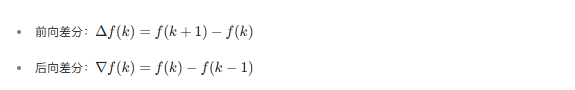
差分方程是描述离散系统输入输出关系的数学表达式,形如:
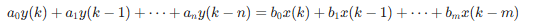
综合案例:差分运算与差分方程示例
import numpy as np
import matplotlib.pyplot as plt
# 配置字体:使用系统中已安装的中文字体(按优先级排列)
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'WenQuanYi Micro Hei']
plt.rcParams['axes.unicode_minus'] = False # 正确显示负号
# 定义离散信号
k = np.arange(0, 10)
f = np.sin(k * 0.5) # 正弦信号
# 计算前向差分
forward_diff = np.diff(f) # np.diff计算相邻元素差值,即前向差分
forward_diff = np.append(forward_diff, 0) # 补零使长度与原信号一致
# 计算后向差分
backward_diff = np.zeros_like(f)
backward_diff[1:] = f[1:] - f[:-1]
# 定义差分方程:y(k) - 0.5y(k-1) = x(k)
def difference_equation(x, y_prev=0):
"""求解一阶差分方程 y(k) - 0.5y(k-1) = x(k)"""
y = 0.5 * y_prev + x
return y
# 生成输入信号
x = np.ones_like(k) # 单位阶跃信号
# 迭代求解差分方程
y = np.zeros_like(k)
for i in range(len(k)):
if i == 0:
y[i] = difference_equation(x[i]) # 初始条件y(-1)=0
else:
y[i] = difference_equation(x[i], y[i-1])
# 绘制结果
plt.figure(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.stem(k, f, linefmt='r-', markerfmt='ro', basefmt='r-')
plt.title('原始信号 f(k)')
plt.xlabel('k')
plt.ylabel('幅度')
plt.subplot(2, 2, 2)
plt.stem(k, forward_diff, linefmt='g-', markerfmt='go', basefmt='g-')
plt.title('前向差分 Δf(k)')
plt.xlabel('k')
plt.ylabel('幅度')
plt.subplot(2, 2, 3)
plt.stem(k, backward_diff, linefmt='b-', markerfmt='bo', basefmt='b-')
plt.title('后向差分 f(k)')
plt.xlabel('k')
plt.ylabel('幅度')
plt.subplot(2, 2, 4)
plt.stem(k, x, linefmt='m-', markerfmt='mo', basefmt='m-', label='输入x(k)')
plt.stem(k, y, linefmt='c-', markerfmt='co', basefmt='c-', label='输出y(k)')
plt.title('差分方程求解结果')
plt.xlabel('k')
plt.ylabel('幅度')
plt.legend()
plt.tight_layout()
plt.show()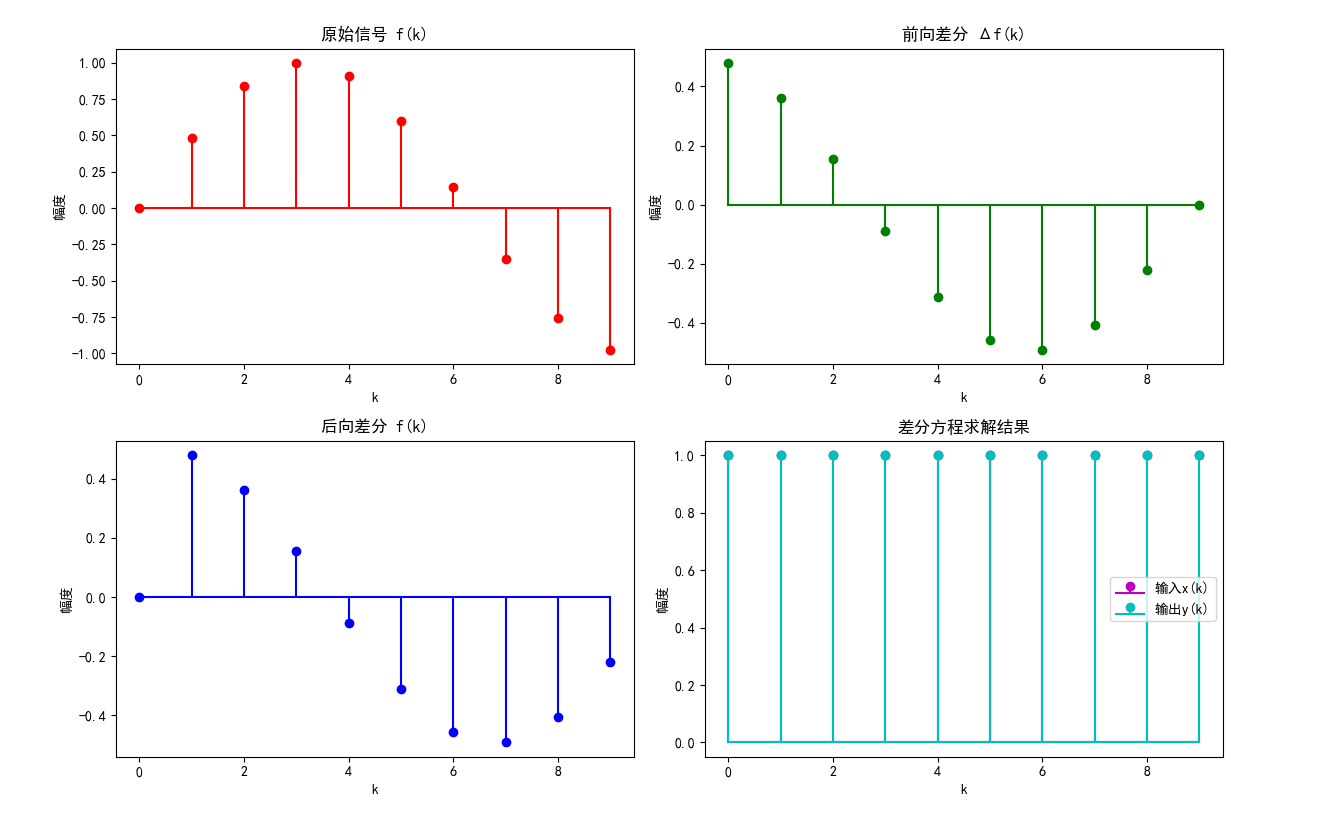
二、差分方程的经典解
差分方程的经典解由齐次解和特解组成:
- 齐次解:对应齐次方程的解,由特征根决定
- 特解:由输入信号形式决定的特解
综合案例:差分方程经典解求解
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义符号变量
k = sp.Symbol('k')
y = sp.Function('y')(k)
# 定义差分方程:y(k) - 3y(k-1) + 2y(k-2) = k
eq = y - 3*sp.Function('y')(k-1) + 2*sp.Function('y')(k-2) - k
# 求解齐次方程:y(k) - 3y(k-1) + 2y(k-2) = 0
homogeneous_eq = y - 3*sp.Function('y')(k-1) + 2*sp.Function('y')(k-2)
homogeneous_sol = sp.rsolve(homogeneous_eq, y, [sp.Function('y')(0), sp.Function('y')(1)])
print("齐次解:", homogeneous_sol)
# 假设特解形式:由于输入为k(一次多项式),且差分方程特征根包含1
# 特解应假设为 k*(Ak + B) = A*k**2 + B*k
A, B = sp.symbols('A B')
particular_sol = A*k**2 + B*k
# 代入差分方程求解特解系数
substituted = particular_sol - 3*particular_sol.subs(k, k-1) + 2*particular_sol.subs(k, k-2) - k
# 整理方程并求解系数
coeffs = substituted.as_poly(k).all_coeffs()
eq_coeffs = sp.solve([coeffs[0], coeffs[1]], [A, B])
# 构建特解
particular_sol = eq_coeffs[A]*k**2 + eq_coeffs[B]*k
print("特解:", particular_sol)
# 通解 = 齐次解 + 特解
general_sol = homogeneous_sol + particular_sol
print("通解:", general_sol)
# 应用初始条件求解常数(假设y(0)=0, y(1)=1)
c1, c2 = sp.symbols('C1 C2')
general_sol = general_sol.subs({sp.Function('y')(0): c1, sp.Function('y')(1): c2})
# 代入k=0和k=1求解c1和c2
eq1 = general_sol.subs(k, 0) - 0
eq2 = general_sol.subs(k, 1) - 1
constants = sp.solve([eq1, eq2], [c1, c2])
final_sol = general_sol.subs(constants)
print("最终解:", final_sol)
# 生成数值解用于绘图
k_vals = np.arange(0, 10)
y_vals = [final_sol.subs(k, i).evalf() for i in k_vals]
# 绘制结果
plt.figure(figsize=(8, 6))
markerline, stemlines, baseline = plt.stem(k_vals, y_vals)
plt.setp(stemlines, color='b', linestyle='-') # 设置茎线颜色和样式
plt.setp(markerline, color='b', marker='o') # 设置标记点颜色和样式
plt.setp(baseline, visible=False) # 隐藏基线
plt.title('差分方程经典解')
plt.xlabel('k')
plt.ylabel('y(k)')
plt.grid(True, alpha=0.3)
plt.show()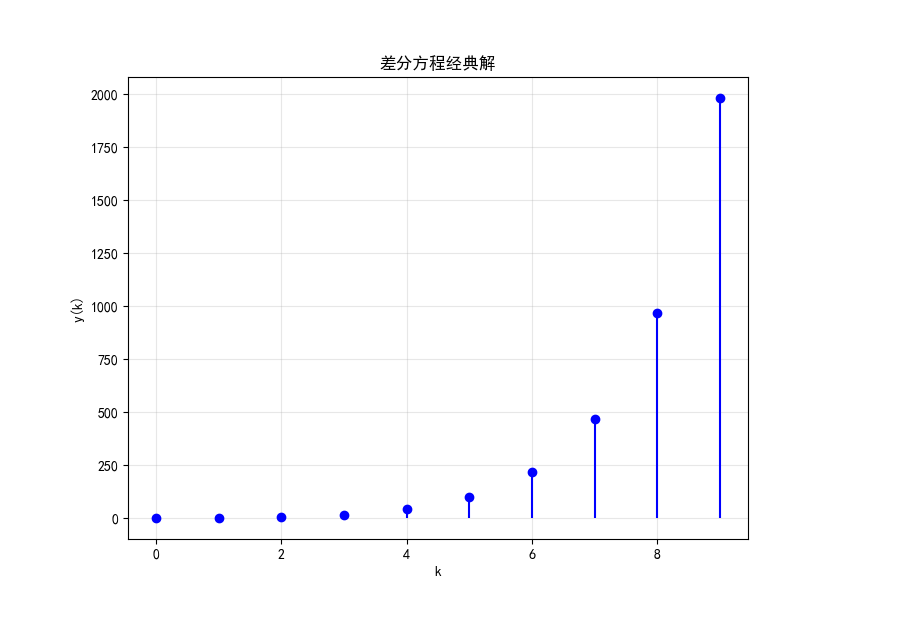
三、零输入响应
零输入响应是指系统在没有输入信号时,仅由初始状态引起的响应,求解步骤:
- 建立齐次方程
- 求特征根,得到齐次解形式
- 利用初始条件确定系数
综合案例:零输入响应计算
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义系统:y(k) - 0.8y(k-1) = x(k),初始条件y(-1)=1
def zero_input_response(n, y_prev):
"""计算零输入响应(x(k)=0)"""
y = np.zeros(n)
y[0] = 0.8 * y_prev # 初始时刻k=0的响应
for i in range(1, n):
y[i] = 0.8 * y[i-1]
return y
# 计算k=0到k=19的零输入响应
n = 20
y_zi = zero_input_response(n, y_prev=1)
k = np.arange(n)
# 绘制零输入响应
plt.figure(figsize=(8, 6))
markerline, stemlines, baseline = plt.stem(k, y_zi)
plt.setp(stemlines, color='r', linestyle='-') # 设置茎线颜色和样式
plt.setp(markerline, color='r', marker='o') # 设置标记点颜色和样式
plt.setp(baseline, visible=False) # 隐藏基线
plt.title('零输入响应')
plt.xlabel('k')
plt.ylabel('y_zi(k)')
plt.grid(True, alpha=0.3)
plt.show()
# 理论解验证:特征根r=0.8,零输入响应y_zi(k) = C*(0.8)^k
# 初始条件y(-1)=1 → y(0)=0.8*1=0.8 = C*(0.8)^0 → C=0.8
# 所以y_zi(k) = 0.8*(0.8)^k = (0.8)^(k+1)
theoretical = (0.8)**(k+1)
# 验证误差
error = np.abs(y_zi - theoretical).max()
print(f"零输入响应理论解:y_zi(k) = (0.8)^(k+1)")
print(f"计算结果与理论解的最大误差:{error}")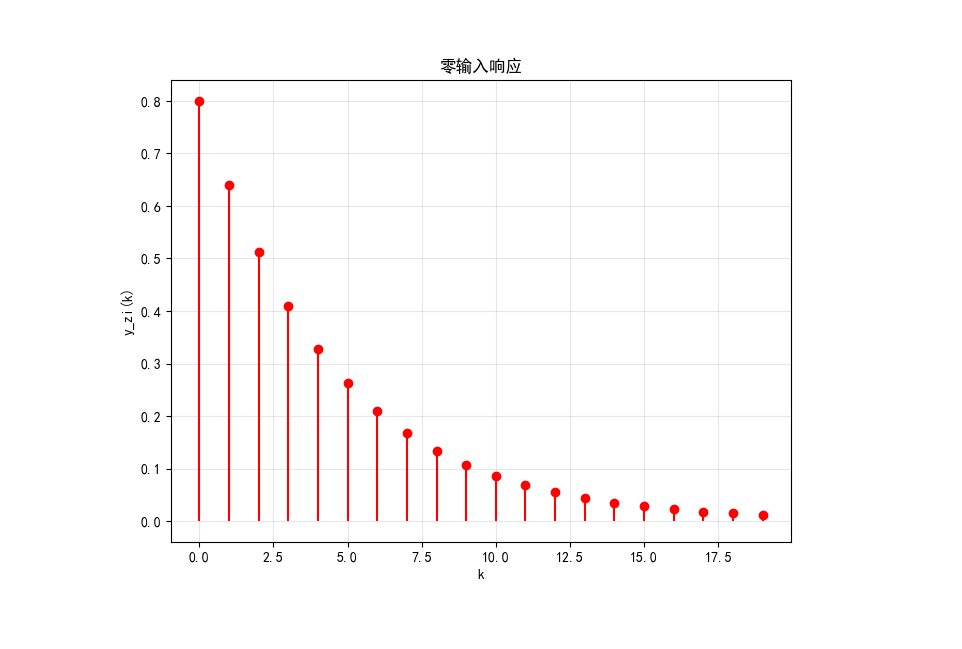
四、零状态响应
零状态响应是指系统初始状态为零时,仅由输入信号引起的响应,通常通过卷积和计算(后续详细介绍)。
综合案例:零状态响应计算
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义系统单位序列响应h(k) = (0.5)^k u(k)
def unit_response(k):
return (0.5)**k * (k >= 0)
# 定义输入信号x(k) = u(k) - u(k-5)(矩形脉冲)
def input_signal(k):
return (k >= 0) & (k < 5)
# 计算零状态响应(通过卷积和)
k = np.arange(0, 15)
h = unit_response(k)
x = input_signal(k)
y_zs = np.convolve(x, h, mode='full')[:len(k)] # 截取与k等长的部分
# 绘制结果
plt.figure(figsize=(10, 6))
# 第一个子图:单位序列响应
plt.subplot(3, 1, 1)
markerline, stemlines, baseline = plt.stem(k, h)
plt.setp(stemlines, color='g', linestyle='-')
plt.setp(markerline, color='g', marker='o')
plt.setp(baseline, visible=False)
plt.title('单位序列响应 h(k)')
plt.xlabel('k')
plt.ylabel('幅度')
# 第二个子图:输入信号
plt.subplot(3, 1, 2)
markerline, stemlines, baseline = plt.stem(k, x)
plt.setp(stemlines, color='b', linestyle='-')
plt.setp(markerline, color='b', marker='o')
plt.setp(baseline, visible=False)
plt.title('输入信号 x(k)')
plt.xlabel('k')
plt.ylabel('幅度')
# 第三个子图:零状态响应
plt.subplot(3, 1, 3)
markerline, stemlines, baseline = plt.stem(k, y_zs)
plt.setp(stemlines, color='r', linestyle='-')
plt.setp(markerline, color='r', marker='o')
plt.setp(baseline, visible=False)
plt.title('零状态响应 y_zs(k)')
plt.xlabel('k')
plt.ylabel('幅度')
plt.tight_layout()
plt.show()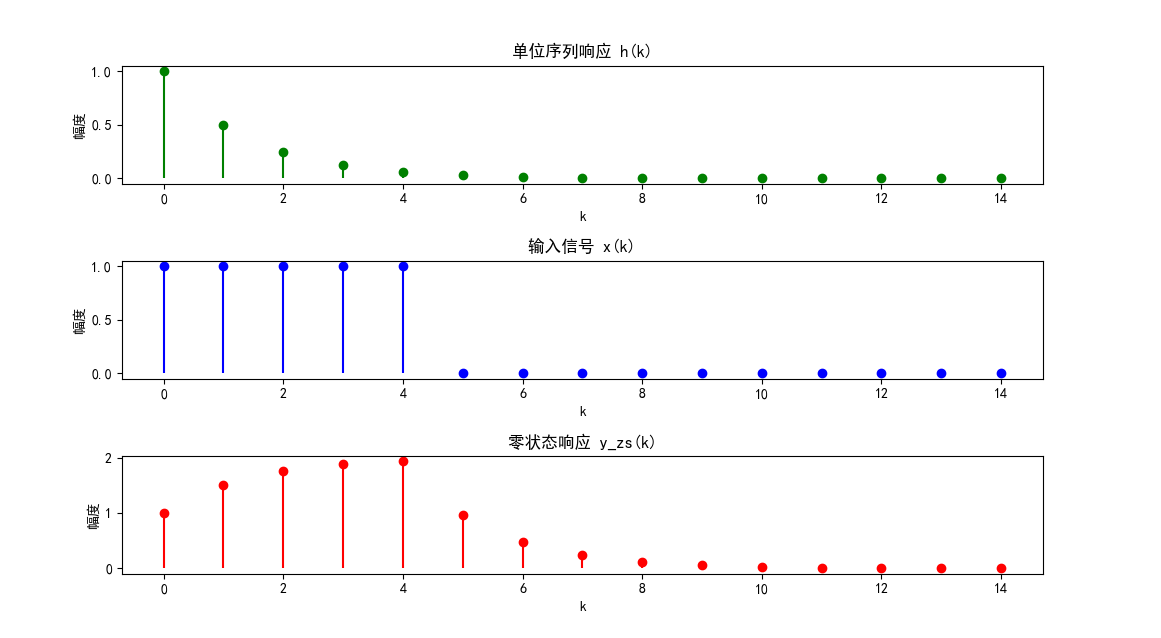
3.2 单位序列和单位序列响应
一、单位序列和单位阶跃序列
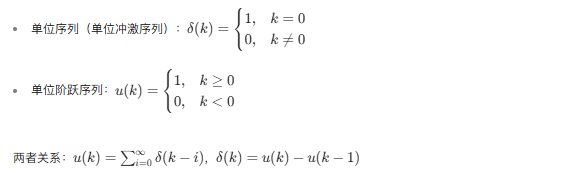
综合案例:单位序列与单位阶跃序列生成
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 生成序列的范围
k = np.arange(-5, 6)
# 定义单位序列δ(k)
def delta(k):
return (k == 0).astype(int)
# 定义单位阶跃序列u(k)
def unit_step(k):
return (k >= 0).astype(int)
# 计算序列值
delta_seq = delta(k)
unit_step_seq = unit_step(k)
# 绘制结果
plt.figure(figsize=(12, 5))
# 第一个子图:单位序列
plt.subplot(1, 2, 1)
markerline, stemlines, baseline = plt.stem(k, delta_seq)
plt.setp(stemlines, color='r', linestyle='-')
plt.setp(markerline, color='r', marker='o')
plt.setp(baseline, visible=False)
plt.title('单位序列 δ(k)')
plt.xlabel('k')
plt.ylabel('幅度')
plt.ylim(-0.1, 1.1)
# 第二个子图:单位阶跃序列
plt.subplot(1, 2, 2)
markerline, stemlines, baseline = plt.stem(k, unit_step_seq)
plt.setp(stemlines, color='b', linestyle='-')
plt.setp(markerline, color='b', marker='o')
plt.setp(baseline, visible=False)
plt.title('单位阶跃序列 u(k)')
plt.xlabel('k')
plt.ylabel('幅度')
plt.ylim(-0.1, 1.1)
plt.tight_layout()
plt.show()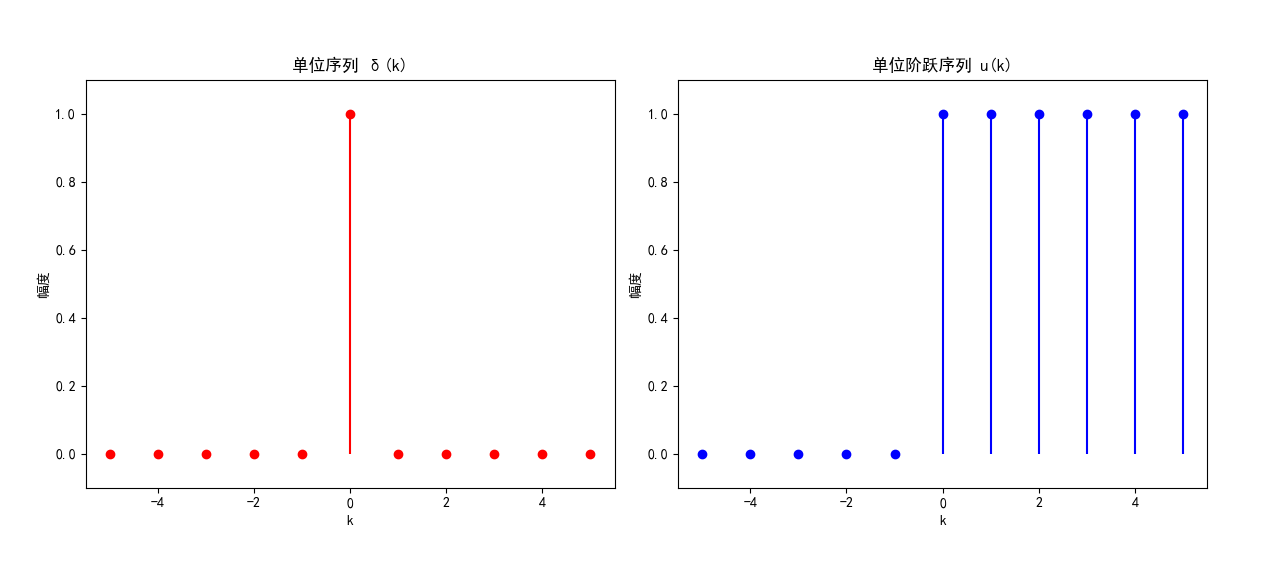
二、单位序列响应和阶跃响应
- 单位序列响应(h (k)):系统对单位序列 δ(k) 的零状态响应
- 阶跃响应(g (k)):系统对单位阶跃序列 u (k) 的零状态响应
两者关系:
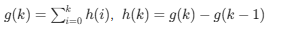
综合案例:单位序列响应与阶跃响应计算
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义系统差分方程:y(k) - 0.6y(k-1) = x(k)
def system_response(x):
"""计算系统对输入x的零状态响应"""
y = np.zeros_like(x)
for i in range(len(x)):
if i == 0:
y[i] = x[i]
else:
y[i] = 0.6 * y[i-1] + x[i]
return y
# 生成单位序列δ(k)
k = np.arange(0, 15)
delta = np.zeros_like(k)
delta[0] = 1
# 计算单位序列响应h(k)
h = system_response(delta)
# 计算阶跃响应g(k)(输入为u(k))
u = np.ones_like(k)
g = system_response(u)
# 验证关系:g(k) = sum(h(0:k))
g_from_h = np.cumsum(h) # 累积和
# 绘制结果
plt.figure(figsize=(12, 8))
# 第一个子图:单位序列响应
plt.subplot(2, 2, 1)
markerline, stemlines, baseline = plt.stem(k, h)
plt.setp(stemlines, color='r', linestyle='-')
plt.setp(markerline, color='r', marker='o')
plt.setp(baseline, visible=False)
plt.title('单位序列响应 h(k)')
plt.xlabel('k')
plt.ylabel('幅度')
# 第二个子图:阶跃响应
plt.subplot(2, 2, 2)
markerline, stemlines, baseline = plt.stem(k, g)
plt.setp(stemlines, color='b', linestyle='-')
plt.setp(markerline, color='b', marker='o')
plt.setp(baseline, visible=False)
plt.title('阶跃响应 g(k)')
plt.xlabel('k')
plt.ylabel('幅度')
# 第三个子图:由h(k)累加得到的g(k)
plt.subplot(2, 2, 3)
markerline, stemlines, baseline = plt.stem(k, g_from_h)
plt.setp(stemlines, color='g', linestyle='-')
plt.setp(markerline, color='g', marker='o')
plt.setp(baseline, visible=False)
plt.title('由h(k)累加得到的g(k)')
plt.xlabel('k')
plt.ylabel('幅度')
# 第四个子图:误差显示
plt.subplot(2, 2, 4)
error = np.abs(g - g_from_h).max()
plt.text(0.5, 0.5, f"最大误差: {error}", fontsize=12, ha='center')
plt.axis('off')
plt.tight_layout()
plt.show()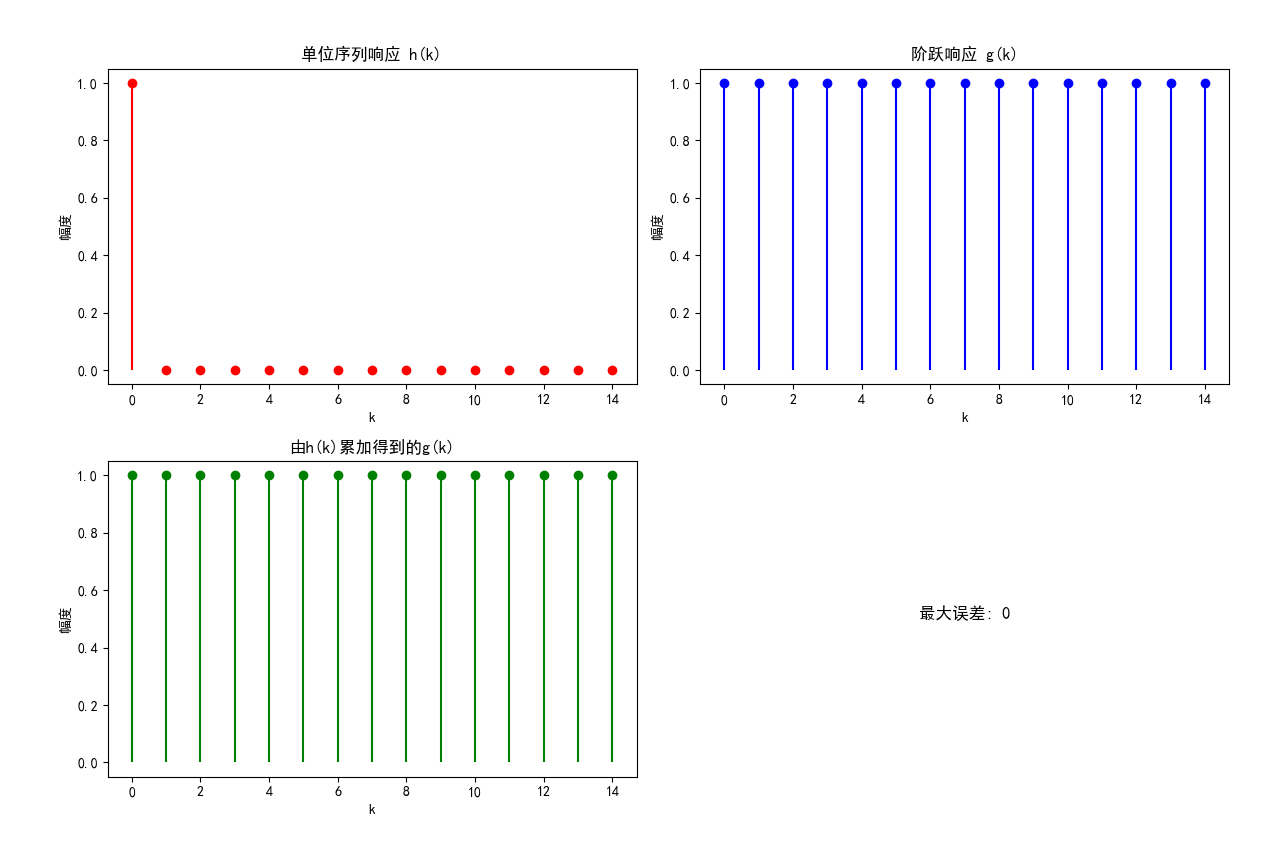
3.3 零状态响应与卷积和
一、任意激励下的零状态响应
对于 LTI 离散系统,任意输入 x (k) 的零状态响应可表示为:
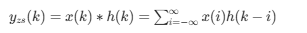
综合案例:任意输入下的零状态响应计算
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义系统单位序列响应h(k) = (0.8)^k u(k)
def h(k):
return (0.8)**k * (k >= 0)
# 定义输入信号x(k) = k*0.5^k u(k)
def x(k):
return k * (0.5)**k * (k >= 0)
# 计算零状态响应(卷积和)
k = np.arange(0, 15)
h_vals = h(k)
x_vals = x(k)
y_zs = np.convolve(x_vals, h_vals, mode='full')[:len(k)] # 截取有效长度
# 绘制结果
plt.figure(figsize=(12, 6))
# 第一个子图:单位序列响应
plt.subplot(1, 3, 1)
markerline, stemlines, baseline = plt.stem(k, h_vals)
plt.setp(stemlines, color='g', linestyle='-')
plt.setp(markerline, color='g', marker='o')
plt.setp(baseline, visible=False)
plt.title('单位序列响应 h(k)')
plt.xlabel('k')
plt.ylabel('幅度')
# 第二个子图:输入信号
plt.subplot(1, 3, 2)
markerline, stemlines, baseline = plt.stem(k, x_vals)
plt.setp(stemlines, color='b', linestyle='-')
plt.setp(markerline, color='b', marker='o')
plt.setp(baseline, visible=False)
plt.title('输入信号 x(k)')
plt.xlabel('k')
plt.ylabel('幅度')
# 第三个子图:零状态响应
plt.subplot(1, 3, 3)
markerline, stemlines, baseline = plt.stem(k, y_zs)
plt.setp(stemlines, color='r', linestyle='-')
plt.setp(markerline, color='r', marker='o')
plt.setp(baseline, visible=False)
plt.title('零状态响应 y_zs(k)')
plt.xlabel('k')
plt.ylabel('幅度')
plt.tight_layout()
plt.show()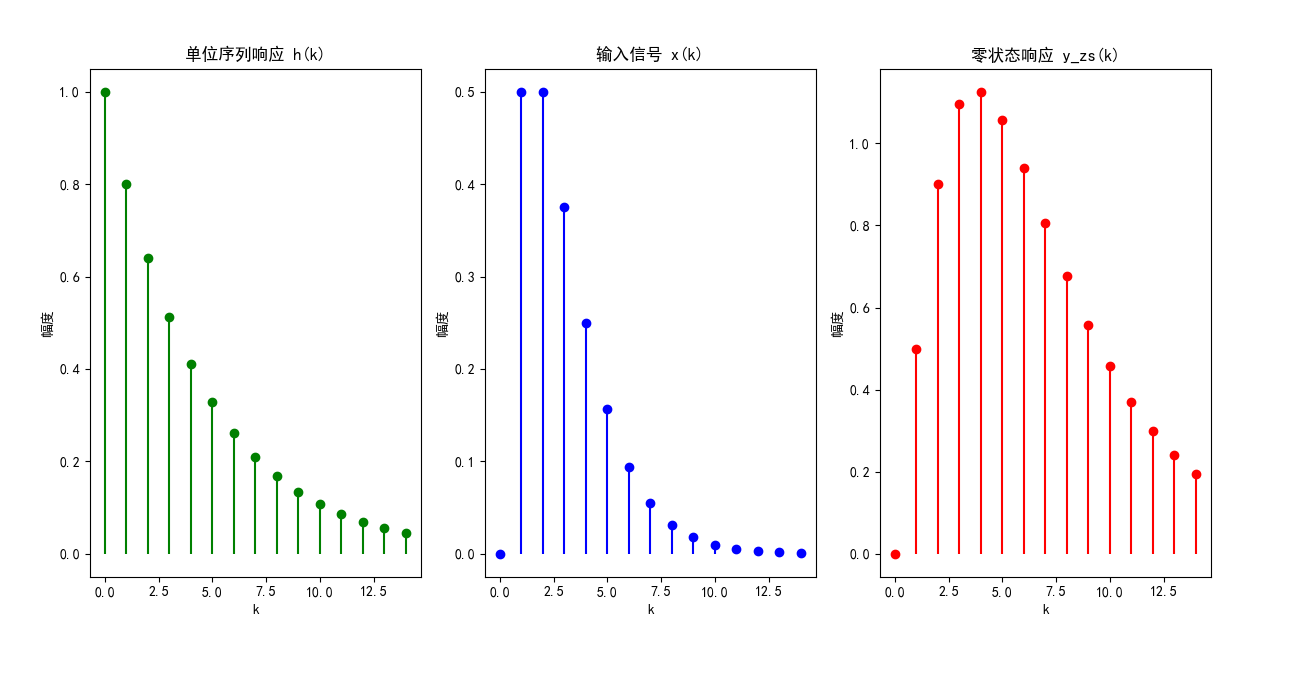
二、卷积和
卷积和是离散信号处理的核心运算,定义为:
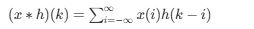
综合案例:卷积和手动计算与 Python 实现
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义信号x(k)和h(k)
k_x = np.arange(0, 4) # x(k)的时间范围
x = np.array([1, 2, 3, 4]) # x(k)的值
k_h = np.arange(0, 3) # h(k)的时间范围
h = np.array([1, 1, 1]) # h(k)的值
# 手动计算卷积和
def manual_convolve(x, h):
"""手动计算卷积和"""
n = len(x) + len(h) - 1
y = np.zeros(n)
for k in range(n):
for i in range(len(x)):
j = k - i
if 0 <= j < len(h):
y[k] += x[i] * h[j]
return y
# 使用numpy的convolve函数计算卷积和
y_np = np.convolve(x, h, mode='full')
# 手动计算结果
y_manual = manual_convolve(x, h)
# 生成卷积和的时间轴
k_y = np.arange(len(y_np))
# 绘制结果
plt.figure(figsize=(12, 6))
# 第一个子图:信号x(k)
plt.subplot(2, 2, 1)
markerline, stemlines, baseline = plt.stem(k_x, x)
plt.setp(stemlines, color='b', linestyle='-')
plt.setp(markerline, color='b', marker='o')
plt.setp(baseline, visible=False)
plt.title('信号 x(k)')
plt.xlabel('k')
plt.ylabel('幅度')
# 第二个子图:信号h(k)
plt.subplot(2, 2, 2)
markerline, stemlines, baseline = plt.stem(k_h, h)
plt.setp(stemlines, color='g', linestyle='-')
plt.setp(markerline, color='g', marker='o')
plt.setp(baseline, visible=False)
plt.title('信号 h(k)')
plt.xlabel('k')
plt.ylabel('幅度')
# 第三个子图:卷积和结果
plt.subplot(2, 2, 3)
markerline_manual, stemlines_manual, baseline = plt.stem(k_y, y_manual)
plt.setp(stemlines_manual, color='r', linestyle='-')
plt.setp(markerline_manual, color='r', marker='o')
markerline_np, stemlines_np, _ = plt.stem(k_y, y_np)
plt.setp(stemlines_np, color='c', linestyle='--')
plt.setp(markerline_np, color='c', marker='o')
plt.title('卷积和 x(k)*h(k)')
plt.xlabel('k')
plt.ylabel('幅度')
plt.legend(['手动计算', 'numpy.convolve'])
# 打印计算结果
print("手动计算卷积和结果:", y_manual)
print("numpy.convolve计算结果:", y_np)
print("结果一致性:", np.allclose(y_manual, y_np))
plt.tight_layout()
plt.show()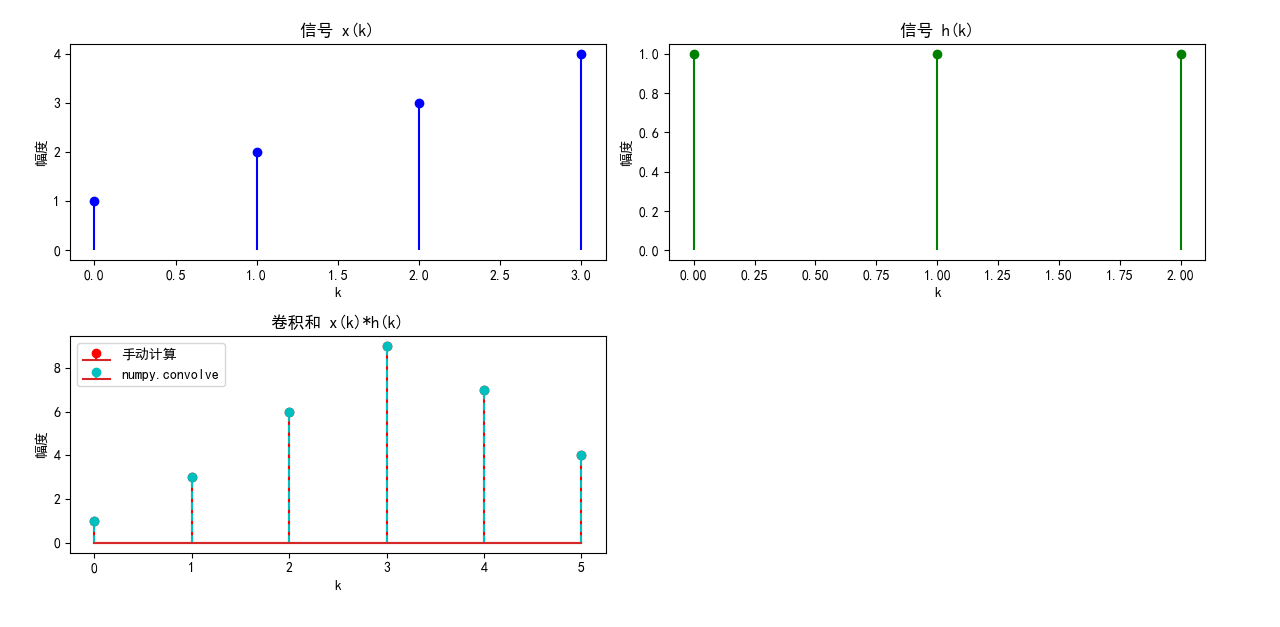
三、卷积和的性质
卷积和具有以下重要性质:
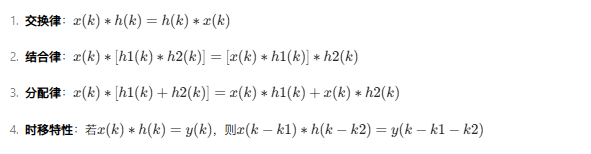
综合案例:卷积和性质验证
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义信号x(k), h1(k), h2(k)
k = np.arange(0, 5)
x = np.array([1, 2, 1, 1])
h1 = np.array([1, 1])
h2 = np.array([1, 0, 1])
# 调整h1和h2的长度一致(以最长数组为准)
max_len_h = max(len(h1), len(h2))
h1_padded = np.pad(h1, (0, max_len_h - len(h1))) # 对h1进行零填充
h2_padded = np.pad(h2, (0, max_len_h - len(h2))) # 对h2进行零填充
# 1. 验证交换律
y_xh = np.convolve(x, h1, mode='full')
y_hx = np.convolve(h1, x, mode='full')
# 2. 验证结合律
y1 = np.convolve(x, np.convolve(h1, h2, mode='full'), mode='full')
y2 = np.convolve(np.convolve(x, h1, mode='full'), h2, mode='full')
# 3. 验证分配律
h_sum = h1_padded + h2_padded # 现在可以相加
y_dist1 = np.convolve(x, h_sum, mode='full')
y_dist2_1 = np.convolve(x, h1, mode='full')
y_dist2_2 = np.convolve(x, h2, mode='full')
# 调整卷积结果长度一致
max_len_conv = max(len(y_dist2_1), len(y_dist2_2))
y_dist2_1_padded = np.pad(y_dist2_1, (0, max_len_conv - len(y_dist2_1)))
y_dist2_2_padded = np.pad(y_dist2_2, (0, max_len_conv - len(y_dist2_2)))
y_dist2 = y_dist2_1_padded + y_dist2_2_padded
# 4. 验证时移特性
x_delay = np.concatenate([np.zeros(2), x]) # x(k-2)
h_delay = np.concatenate([np.zeros(1), h1]) # h1(k-1)
y_original = np.convolve(x, h1, mode='full')
y_delay = np.convolve(x_delay, h_delay, mode='full')
# 绘制结果
plt.figure(figsize=(15, 10))
# 交换律验证
plt.subplot(4, 2, 1)
markerline_xh, stemlines_xh, baseline = plt.stem(np.arange(len(y_xh)), y_xh)
plt.setp(stemlines_xh, color='b', linestyle='-')
plt.setp(markerline_xh, color='b', marker='o')
markerline_hx, stemlines_hx, _ = plt.stem(np.arange(len(y_hx)), y_hx)
plt.setp(stemlines_hx, color='r', linestyle='--')
plt.setp(markerline_hx, color='r', marker='o')
plt.title('交换律验证')
plt.xlabel('k')
plt.ylabel('幅度')
plt.legend(['x*h1', 'h1*x'])
plt.subplot(4, 2, 2)
error = np.abs(y_xh - y_hx).max()
plt.text(0.5, 0.5, f"交换律误差: {error}", fontsize=12, ha='center')
plt.axis('off')
# 结合律验证
plt.subplot(4, 2, 3)
markerline_y1, stemlines_y1, baseline = plt.stem(np.arange(len(y1)), y1)
plt.setp(stemlines_y1, color='b', linestyle='-')
plt.setp(markerline_y1, color='b', marker='o')
markerline_y2, stemlines_y2, _ = plt.stem(np.arange(len(y2)), y2)
plt.setp(stemlines_y2, color='r', linestyle='--')
plt.setp(markerline_y2, color='r', marker='o')
plt.title('结合律验证')
plt.xlabel('k')
plt.ylabel('幅度')
plt.legend(['x*(h1*h2)', '(x*h1)*h2'])
plt.subplot(4, 2, 4)
error = np.abs(y1 - y2).max()
plt.text(0.5, 0.5, f"结合律误差: {error}", fontsize=12, ha='center')
plt.axis('off')
# 分配律验证
plt.subplot(4, 2, 5)
y_dist1 = np.convolve(x, h_sum, mode='full')
markerline_dist1, stemlines_dist1, baseline = plt.stem(np.arange(len(y_dist1)), y_dist1)
plt.setp(stemlines_dist1, color='b', linestyle='-')
plt.setp(markerline_dist1, color='b', marker='o')
markerline_dist2, stemlines_dist2, _ = plt.stem(np.arange(len(y_dist2)), y_dist2)
plt.setp(stemlines_dist2, color='r', linestyle='--')
plt.setp(markerline_dist2, color='r', marker='o')
plt.title('分配律验证')
plt.xlabel('k')
plt.ylabel('幅度')
plt.legend(['x*(h1+h2)', 'x*h1 + x*h2'])
plt.subplot(4, 2, 6)
error = np.abs(y_dist1 - y_dist2).max()
plt.text(0.5, 0.5, f"分配律误差: {error}", fontsize=12, ha='center')
plt.axis('off')
# 时移特性验证
plt.subplot(4, 2, 7)
markerline_original, stemlines_original, baseline = plt.stem(np.arange(len(y_original)), y_original)
plt.setp(stemlines_original, color='b', linestyle='-')
plt.setp(markerline_original, color='b', marker='o')
markerline_delay, stemlines_delay, _ = plt.stem(np.arange(len(y_delay)), y_delay)
plt.setp(stemlines_delay, color='r', linestyle='--')
plt.setp(markerline_delay, color='r', marker='o')
plt.title('时移特性验证')
plt.xlabel('k')
plt.ylabel('幅度')
plt.legend(['原始卷积', '时移卷积'])
plt.subplot(4, 2, 8)
# 时移后y_delay的有效部分从第3个元素开始
error = np.abs(y_delay[3:] - y_original).max()
plt.text(0.5, 0.5, f"时移特性误差: {error}", fontsize=12, ha='center')
plt.axis('off')
plt.tight_layout()
plt.show()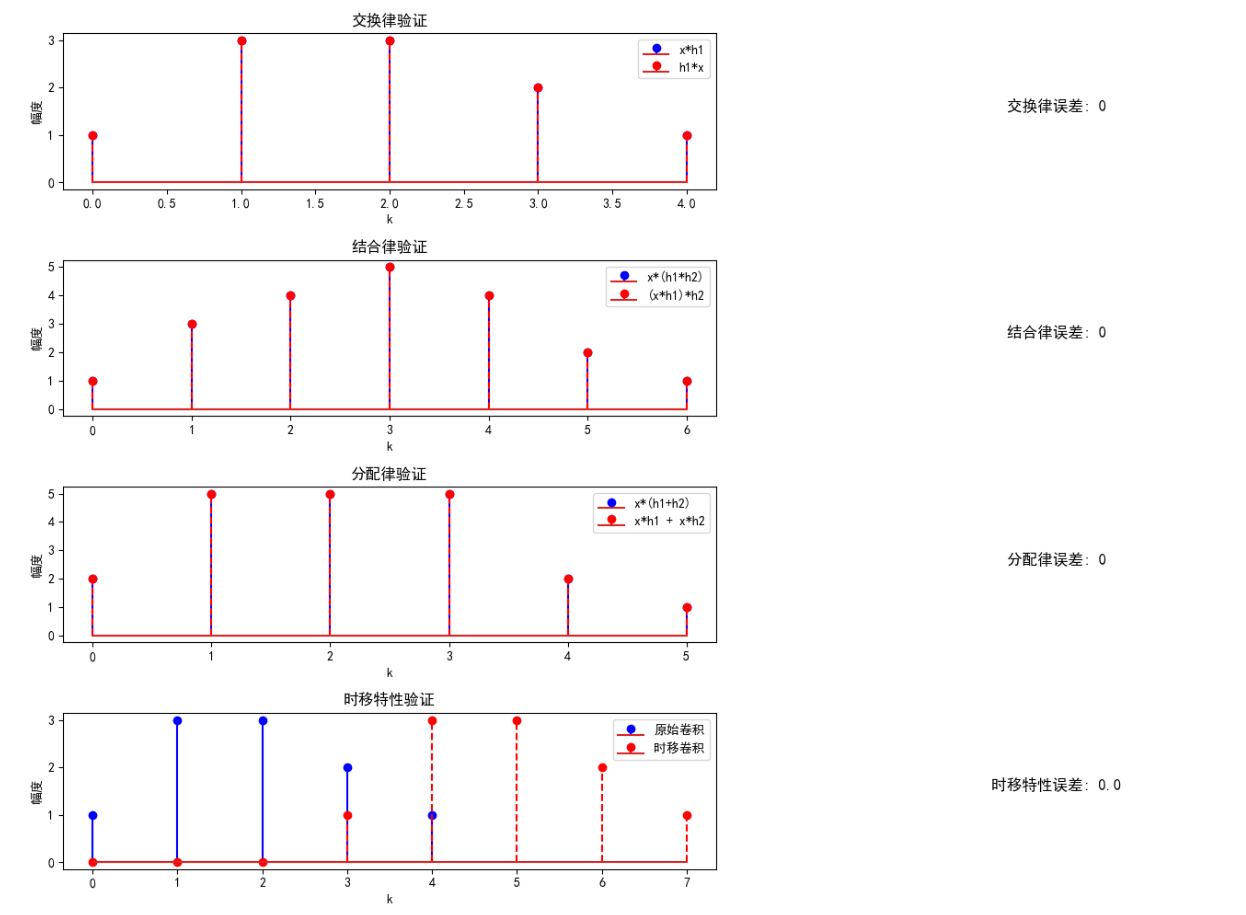
本章思维导图
第三章 离散系统的时域分析

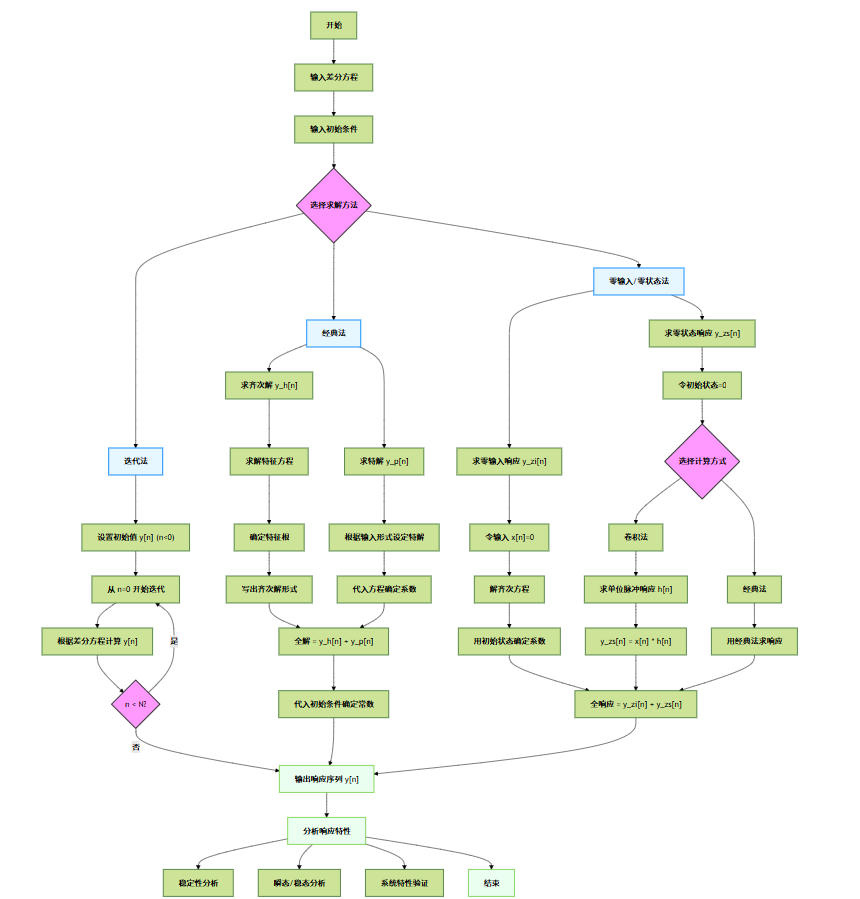
差分方程求解流程图
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-06-30,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

