【数据结构】常见的排序算法 -- 归并排序

小年糕是糕手

发布于 2026-01-14 17:26:03

690

文章被收录于专栏：C++学习C++学习

一、归并排序

1.1、算法思想

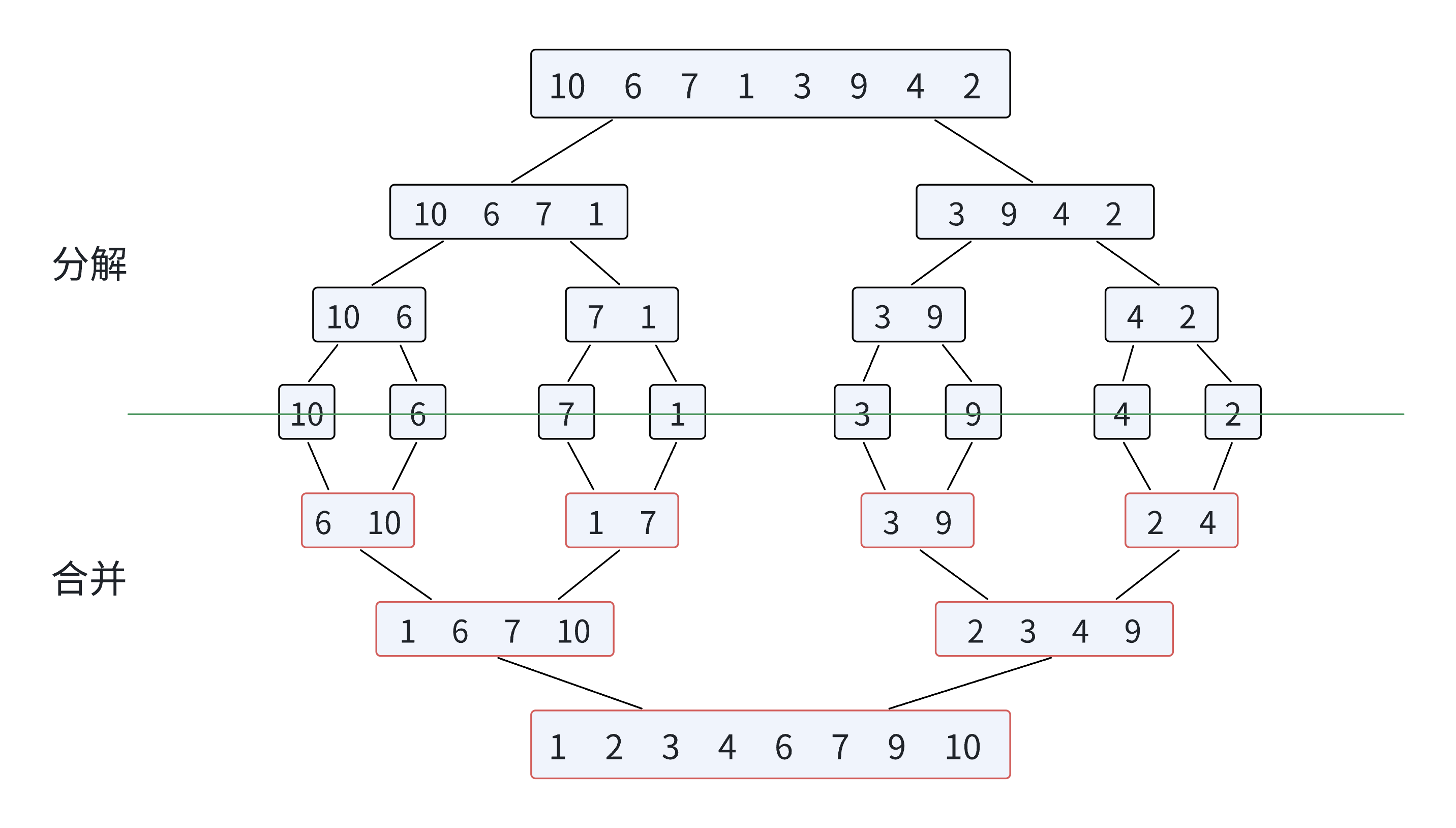
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。归并排序核心步骤：

创建一个临时数组 temp，用于存储合并后的结果。
定义两个指针 i（左子数组起始位置）和 j（右子数组起始位置）。
比较 i 和 j 指向的元素：
- 若左子数组元素更小，将其放入 temp，并移动 i 指针。
- 若右子数组元素更小，将其放入 temp，并移动 j 指针。
将左 / 右子数组中剩余的元素（若有）全部复制到 temp 中。
将 temp 中的有序元素复制回原始数组的对应位置，完成一次合并。

1.2、代码实现

void _MergeSort(int* arr, int left, int right, int* tmp)
{
	//分解
	if (left == right)//换成 >= 也可以
	{
		return;
	}
	int mid = (left + right) / 2;
	//根据mid将[left,right]划分左右俩个序列:[left,mid] [mid+1,right]
	_MergeSort(arr, left, mid, tmp);
	_MergeSort(arr, mid + 1, right, tmp);
	
	//合并俩个序列:[left,mid] [mid+1,right]
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] < arr[begin2])
		{
			tmp[index] = arr[begin1];
			index++;
			begin1++;
		}
		else
		{
			tmp[index] = arr[begin2];
			index++;
			begin2++;
		}
	}
	//要么begin1序列中数据没有放完
	//要么begin2序列中数据没有放完
	while (begin1 <= end1)
	{
		tmp[index] = arr[begin1];
		index++;
		begin1++;
	}
	while (begin2 <= end2)
	{
		tmp[index] = arr[begin2];
		index++;
		begin2++;
	}
	//tmp拷贝回arr
	for (int i = left; i <= right; i++)
	{
		arr[i] = tmp[i];
	}
}

//1)归并排序
void MergeSort(int* arr, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	//[0,n-1]
	_MergeSort(arr, 0, n - 1, tmp);
	free(tmp);
}

归并排序特性总结：

时间复杂度：O(n*logn)
空间复杂度：O(n)

二、排序性能对比（测试代码）

// 测试排序的性能对⽐  
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	BubbleSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
	printf("BubbleSort:%d\n", end7 - begin7);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}

具体的排序算法大家可以参考：插入排序、选择排序、交换排序以及本篇归并排序。

三、排序算法复杂度及稳定性分析

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[ i ] = r[ j ]，且r[ i ]在r[ j ]之前，而在排序后的序列中，r[ i ]仍在r[ j ]之前，则称这种排序算法是稳定的；否则称为不稳定的。

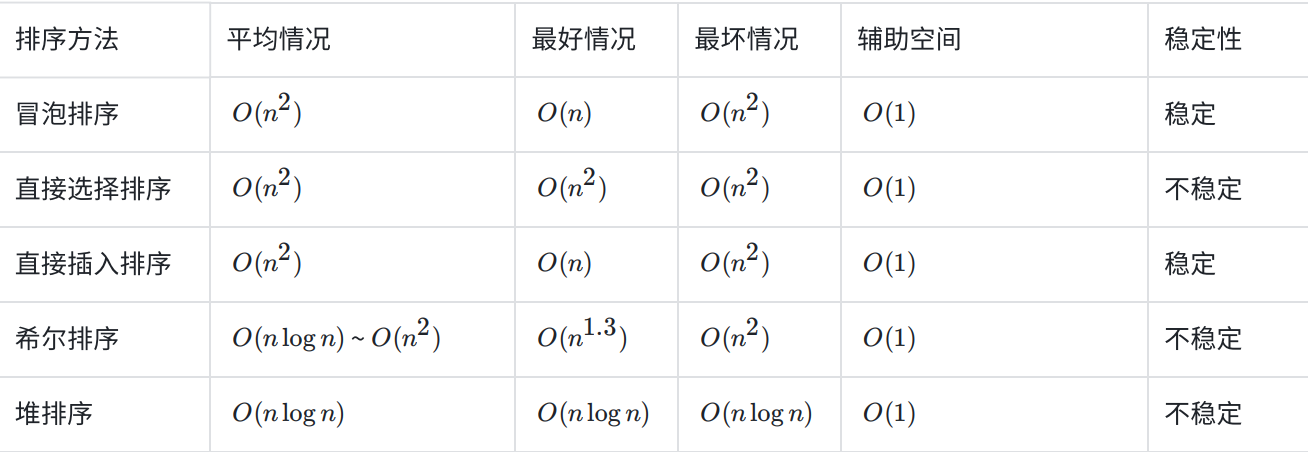
关键结论

稳定性：稳定排序算法能保持相等元素的原有相对顺序（如冒泡、插入、归并、计数、桶、基数），不稳定算法可能改变（如选择、快速、堆）。
空间复杂度：原地排序（O (1) 或 O (log n)）适合内存有限场景（如选择、冒泡、插入、堆、快速），非原地排序需额外空间（如归并、计数、桶、基数）。
适用场景：
- 小规模数据：插入排序、冒泡排序（简单易实现）。
- 大规模数据：快速排序（平均最优）、归并排序（稳定且最坏可预测）。
- 整数 / 范围有限：计数排序、基数排序（效率远超比较排序）。

真正的排序算法不是我们四篇博客就可以说的清楚的，需要我们不断地去写代码的同时不断理解。

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-11-12，如有侵权请联系 cloudcommunity@tencent.com 删除

int