算法基础篇：（二十二）数据结构之单调队列：滑动窗口问题的 “最优解” 神器

前言

在算法竞赛和日常开发中，滑动窗口类问题是高频考点 —— 比如求滑动窗口内的最大值、最小值，或是基于窗口的动态规划优化。如果用暴力解法，时间复杂度往往是 O (nk)（n 为序列长度，k 为窗口大小），面对 1e6 级别的数据时直接超时。而单调队列，正是解决这类问题的 “神兵利器”，能将时间复杂度降至 O (n)，堪称滑动窗口问题的 “最优解”。 本文将从单调队列的核心概念、实现原理、经典模板题到实战应用，全方位拆解这个数据结构，让你从 “懂原理” 到 “能手写”，彻底掌握单调队列的精髓。下面就让我们正式开始吧！

一、什么是单调队列？

在聊单调队列之前，先回忆一下基础数据结构：普通队列是 “先进先出”（FIFO）的线性结构，只能在队尾插入、队头删除；而单调队列，本质是维护了单调性的双端队列（deque） —— 队列内的元素要么严格单调递增，要么严格单调递减，且支持队头 / 队尾的插入、删除操作。

1.1 核心特性

• 双端操作：可以从队头弹出元素（处理窗口越界），也可以从队尾弹出元素（维护单调性）；
• 单调性：队列内元素的 “关键值”（比如数值大小）保持严格递增 / 递减，这是解决问题的核心；
• 存储下标：实际应用中，单调队列通常存储元素的下标而非数值本身 —— 这样既能通过下标获取数值，又能快速判断元素是否在当前窗口内。

1.2 为什么需要单调队列？

以 “滑动窗口最大值” 问题为例：给定序列[1,3,-1,-3,5,3,6,7]，窗口大小 k=3，要求输出每次滑动后的窗口最大值。暴力解法会遍历每个窗口的 k 个元素找最大值，时间复杂度 O (nk)；而单调队列能通过 “淘汰无效元素”，让每个元素只入队、出队一次，最终做到线性时间复杂度。

举个生活化的例子：假设你是面试官，要从排队的候选人中选 “当前窗口内最优秀的人”。如果新来的候选人比队列末尾的人更优秀，那末尾的人永远不可能成为 “最优”，直接淘汰；如果新来的人能力一般，就暂时留在队列里，等前面的人离开窗口后，他可能成为最优。这就是单调队列的核心思想 ——只保留对结果有意义的元素。

二、单调队列的核心操作：维护单调性

单调队列的核心是两个操作：入队和出队，所有逻辑都围绕 “维护队列单调性” 展开。我们以 “维护单调递减队列（求窗口最大值）” 为例，拆解具体步骤。

2.1 入队操作（队尾）

当新元素要加入队列时，需要从队尾开始检查：

• 如果队尾元素的数值 ≤ 新元素的数值：说明队尾元素在后续窗口中，永远不可能成为最大值（因为新元素更大，且位置更靠后），直接弹出队尾元素；
• 重复上述步骤，直到队尾元素 > 新元素，或队列为空；
• 将新元素的下标加入队尾。

2.2 出队操作（队头）

滑动窗口向右移动时，需要检查队头元素是否超出窗口范围：

• 假设当前窗口的左边界是i - k + 1（i 为当前遍历的下标），如果队头元素的下标 < 左边界：说明该元素已不在窗口内，弹出队头；
• 此时队头元素就是当前窗口的最大值。

2.3 可视化演示

以序列[1,3,-1,-3,5,3,6,7]，k=3 为例，模拟单调递减队列的变化：

可以看到：每次窗口滑动后，队头元素都是当前窗口的最大值，且每个元素仅入队、出队一次。

三、经典模板：滑动窗口的最大值 / 最小值

这是单调队列的入门必做题，题目要求同时输出滑动窗口的最小值和最大值。我们以此为例，编写完整的 C++ 代码，并详细注释。

题目链接如下：https://www.luogu.com.cn/problem/P1886

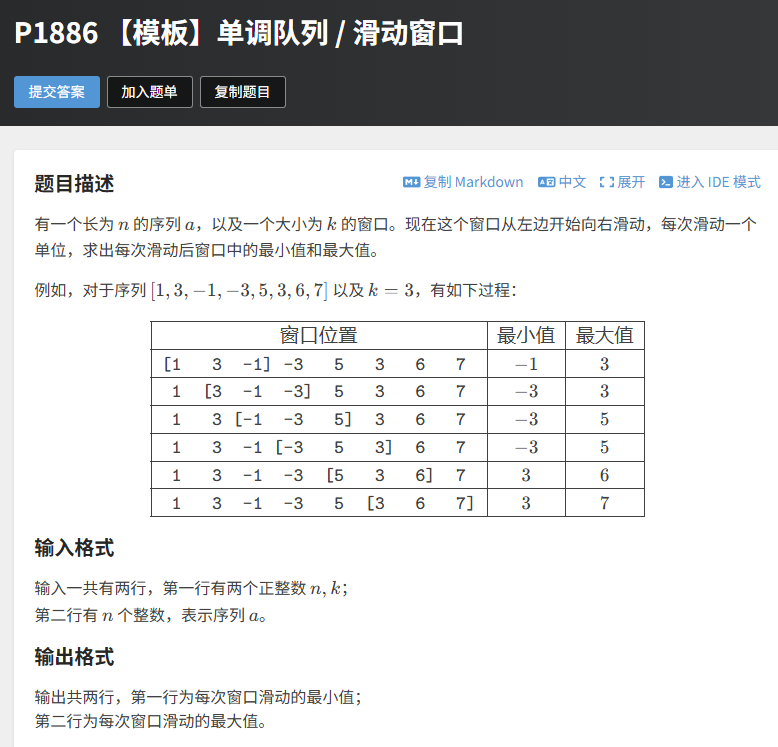
3.1 题目描述

• 输入：n（序列长度）、k（窗口大小），以及长度为 n 的序列 a；
• 输出：第一行是每次窗口滑动后的最小值，第二行是最大值。

3.2 完整代码实现

#include <iostream>
#include <deque>
using namespace std;

const int N = 1e6 + 10; // 数据范围1e6，数组开大点
int a[N]; // 存储原始序列
int n, k; // n是序列长度，k是窗口大小

// 求滑动窗口最小值：维护单调递增队列
void get_min() {
    deque<int> q; // 双端队列，存储元素下标
    for (int i = 1; i <= n; i++) {
        // 1. 维护队列单调性：队尾元素 >= 当前元素，弹出（因为当前元素更小，更有机会成为最小值）
        while (!q.empty() && a[q.back()] >= a[i]) {
            q.pop_back();
        }
        // 2. 加入当前元素下标
        q.push_back(i);
        // 3. 维护窗口范围：队头元素超出窗口左边界，弹出
        while (q.front() <= i - k) {
            q.pop_front();
        }
        // 4. 窗口形成后，输出队头（最小值）
        if (i >= k) {
            cout << a[q.front()] << " ";
        }
    }
    cout << endl;
}

// 求滑动窗口最大值：维护单调递减队列
void get_max() {
    deque<int> q;
    for (int i = 1; i <= n; i++) {
        // 1. 维护队列单调性：队尾元素 <= 当前元素，弹出（当前元素更大，更有机会成为最大值）
        while (!q.empty() && a[q.back()] <= a[i]) {
            q.pop_back();
        }
        // 2. 加入当前元素下标
        q.push_back(i);
        // 3. 维护窗口范围
        while (q.front() <= i - k) {
            q.pop_front();
        }
        // 4. 窗口形成后输出
        if (i >= k) {
            cout << a[q.front()] << " ";
        }
    }
    cout << endl;
}

int main() {
    ios::sync_with_stdio(false); // 加速cin/cout
    cin.tie(0);

    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    get_min();
    get_max();

    return 0;
}

3.3 代码核心解析

1. 加速输入输出：ios::sync_with_stdio(false); cin.tie(0);—— 面对 1e6 级别的数据，必须关闭 cin 与 stdio 的同步，否则会超时；
2. 队列存储下标：而非数值，这样既能通过a[q.front()]获取数值，又能通过下标判断是否超出窗口；
3. 单调性维护：
   • 求最小值：队列单调递增（队头是最小值），队尾≥当前元素则弹出；
   • 求最大值：队列单调递减（队头是最大值），队尾≤当前元素则弹出；
4. 窗口范围判断：q.front() <= i - k—— 窗口左边界是i - k + 1，如果队头下标小于左边界，说明不在窗口内，弹出。

3.4 测试用例验证

输入：

8 3
1 3 -1 -3 5 3 6 7

输出：

-1 -3 -3 -3 3 3 
3 3 5 5 6 7 

与题目要求完全一致，验证了代码的正确性。

四、实战应用：质量检测（洛谷 P2251）

掌握了模板后，我们来看一道变形题 —— 洛谷 P2251《质量检测》，这道题是 “滑动窗口最小值” 的直接应用，只是输出格式略有不同。

题目链接：https://www.luogu.com.cn/problem/P2251

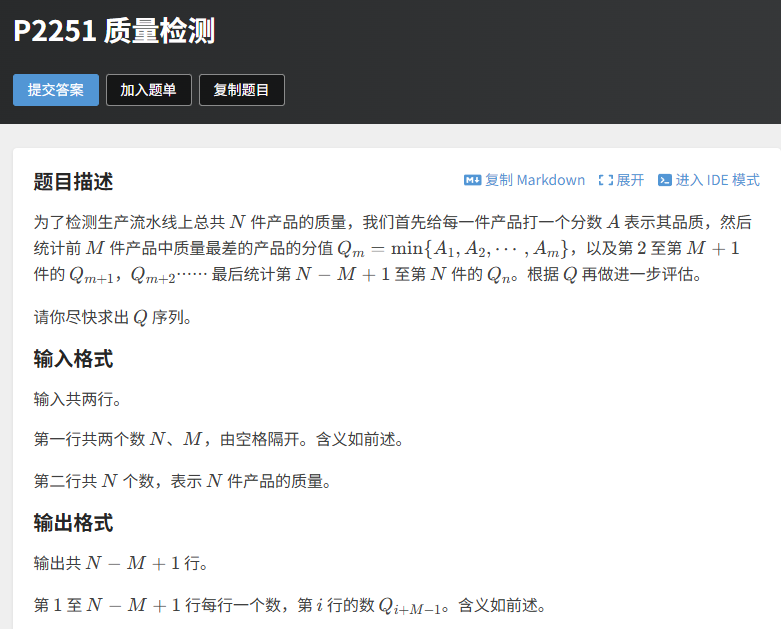
4.1 题目描述

• 输入：N（产品数量）、M（窗口大小），以及 N 个产品的质量分数；
• 输出：共 N-M+1 行，每行是当前窗口的最小值（窗口从第 1 个产品开始，每次右移一位）。

4.2 代码实现

#include <iostream>
#include <deque>
using namespace std;

const int N = 1e6 + 10;
int a[N];
int n, k;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> k;
    deque<int> q; // 单调递增队列，存下标

    for (int i = 1; i <= n; i++) {
        cin >> a[i];

        // 维护单调性：队尾 >= 当前元素，弹出
        while (!q.empty() && a[q.back()] >= a[i]) {
            q.pop_back();
        }
        q.push_back(i);

        // 维护窗口范围
        while (q.front() <= i - k) {
            q.pop_front();
        }

        // 窗口形成后输出（每行一个结果）
        if (i >= k) {
            cout << a[q.front()] << endl;
        }
    }

    return 0;
}

4.3 解题思路

这道题和模板题的核心逻辑完全一致，唯一区别是输出格式：模板题是一行输出所有结果，本题是每行输出一个结果。这也体现了单调队列的灵活性 —— 只要核心逻辑不变，只需调整输出方式即可适配不同题目。

五、单调队列的常见坑点

在实际编码中，新手容易踩以下几个坑，务必注意：

5.1 队列存储数值而非下标

这是最常见的错误！如果存储数值，无法判断该元素是否在当前窗口内，导致窗口范围维护失败。一定要存储下标，数值通过下标获取。

5.2 单调性维护不彻底

比如求最大值时，队尾元素 “≤” 当前元素才弹出，少写了 “=” 会导致队列中出现相等元素，破坏单调性，最终结果错误。

5.3 窗口范围判断错误

窗口左边界的计算：i - k + 1，因此队头下标需要满足q.front() >= i - k + 1，即q.front() <= i - k时弹出。如果写成q.front() < i - k + 1，逻辑等价，但容易混淆，建议记准 “q.front() <= i - k”。

5.4 忘记加速输入输出

面对 1e6 级别的数据，cin/cout 默认速度很慢，最好加上ios::sync_with_stdio(false); cin.tie(0);，否则容易超时。

总结

单调队列是算法学习中 “性价比极高” 的知识点 —— 理解起来简单，代码量少，却能解决一大类高频问题。掌握它的关键是：先理解 “为什么要维护单调性”，再动手模拟队列的变化，最后默写模板并适配不同题目。 建议大家先手动模拟模板题的队列变化过程，再敲代码，最后尝试不看模板写出完整代码。当你能熟练写出滑动窗口最值的代码时，就说明真正掌握了单调队列的精髓。 算法学习没有捷径，唯有 “理解 + 练习”。希望本文能帮你攻克单调队列，在刷题和竞赛中少走弯路～