二叉树的链式结构

1.1C++的第一个程序

1.1概念

用链表来表示一棵二叉树，即用链表来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别来给出该结点左孩子和右孩子所在的链接点的存储地址。

二叉树的链式结构不像之前学的顺序结构，链式结构一般用递归来实现。并且链式结构一般不用来插入或删除数据，因为二叉树不一定就是完全二叉树，插入或删除不能确定位置，所以链式结构一般用来遍历二叉树或查找数据。

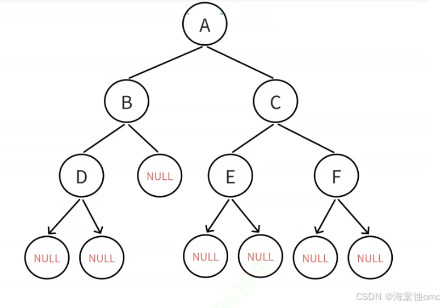
链式结构的遍历方式分为：前序遍历，中序遍历，后序遍历和层序遍历。

前序遍历：先根遍历(先遍历根结点，再去遍历左子树，最后是右子树) ---根左右

中序遍历：先遍历左子树，再遍历根结点，最后是右子树 ---左根右

后序遍历：先遍历左子树，在遍历右子树，最后是根结点 ---左右根

层序遍历：一层一层遍历每个结点

前中后序是比较简单的，层序遍历较难，下面我都会详细介绍。

1.2代码示例

typedef char BTDateType;
typedef struct BinaryTreeNode
{
	BTDateType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

二叉树结点的结构

里面包含了结点中存储的数据，左右子树的地址，这是结点的基本结构。这里因为要用字母来表示每个结点，故数据类型为char。

void preorder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	preorder(root->left);
	preorder(root->right);
}

前序遍历

1.判断此时的根结点是否为空

2.打印出此时根结点的数据

3.通过递归来遍历整个二叉树，以根左右的顺序打印出前序遍历的结果

前序遍历的结果应为：A B D NULL NULL NULL C E NULL NULL F

在前序遍历中，包括中序遍历和后序遍历，printf就是根结点的位置，根据根结点位置的不同来调整位置，递归这种方法是需要画图才好理解，这里我演示一下前序遍历的递归。

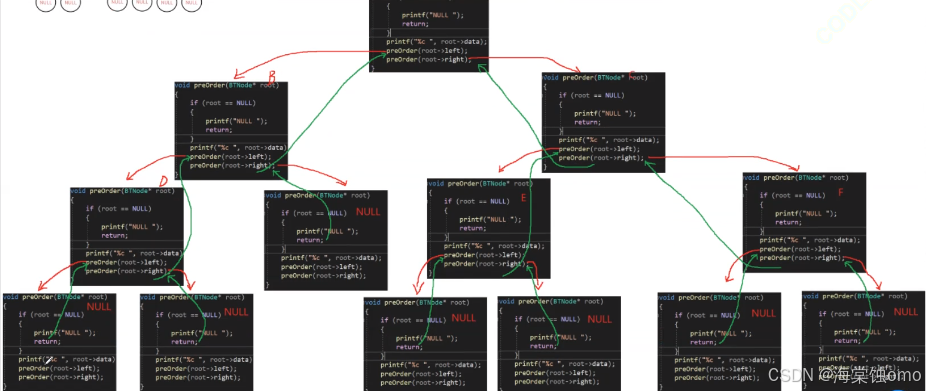
以上面那幅图为例，这就是前序遍历的递归图，最上面就是根结点A，红色的线代表向下递归调用函数，绿色的线代表回溯，每一次递归都需要把代码走完之后才会回溯。

void inorder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	inorder(root->left);
	printf("%c ", root->data);
	inorder(root->right);
}

中序遍历

1.判断此时的根结点是否为空

2.向左递归

3.打印出此时根结点的数据

4.向右递归

与前序遍历不同的就是根结点的位置，中序遍历根结点在中，所以把根结点的位置放在中间即可

中序遍历的结果为：NULL D NULL B NULL A NULL E NULL C NULL F NULL

void postorder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	postorder(root->left);
	postorder(root->right);
	printf("%c ", root->data);
}

后序遍历

1.判断此时的根结点是否为空

2.向左递归

3.向右递归

4打印出此时根结点的数据

与前序遍历不同的就是根结点的位置，后序遍历根结点在后，所以把根结点的位置放在最后即可

后序遍历的结果为：NULL NULL D NULL B NULL NULL E NULL NULL F C A

中序遍历和后序遍历的递归图我就不画了，大家下去可以自己画画或者根据我画的前序遍历的递归图把剩下两个画出来。

int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

二叉树结点个数

要实现这个方法我们要先清楚：二叉树结点个数=根结点+左子树的结点+右子树的结点。

根据这个思路我们就可以写出代码： 1.判断当前结点是否为NULL，是的话返回0

2.通过递归返回二叉树的结点个数

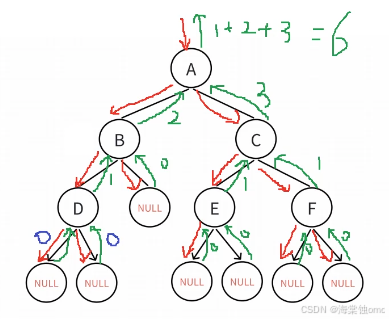
此方法的递归图，红色的线表示向下递归调用函数，绿色的线表示回溯，通过这个递归图就可以清晰明了地看出每次回溯返回的值是多少，之后让每次回溯的值相加就得到了二叉树结点的个数。

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

二叉树叶子节点的个数

要实现此方法我们要清楚：叶子结点个数=左子树叶子结点个数+右子树叶子结点个数，叶子结点的左右子树都为NULL，符合这一点，我们就返回1。

根据这个思路我们就可以写出代码： 1.判断当前结点是否为NULL，是的话返回0

2.如果符合叶子结点的特征，就返回1

3..通过递归返回二叉树的叶子结点个数

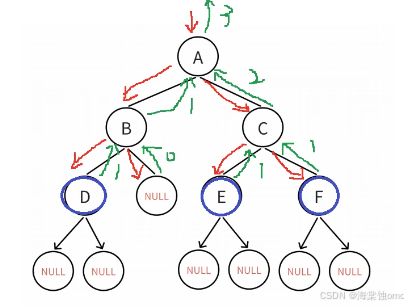
此方法的递归图，由图我们可以看出当递归到叶子节点时，判断符合条件，就返回1进行回溯，最后将左子树的叶子结点个数和右子树的叶子结点个数相加即可。

int BinaryTreelevelSize(BTNode* root,int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreelevelSize(root->left, k - 1) + BinaryTreelevelSize(root->right, k - 1);
}

二叉树第k层的结点个数

此方法的思路是：我们给定一个数k，递归向下一层，我们就让k-1，当k=1时就到了我们要找的那层，并且符合当前结点不为NULL和k=1，我们就返回1，最后将左子树属于k层的结点个数和右子树属于k层的结点个数相加即可。

根据这个思路我们就可以写出代码：

1.判断当前节点是否为NULL

2.判断k是否等于1，并且符合结点不为NULL的情况下，返回1

3.通过递归返回第k层的结点个数

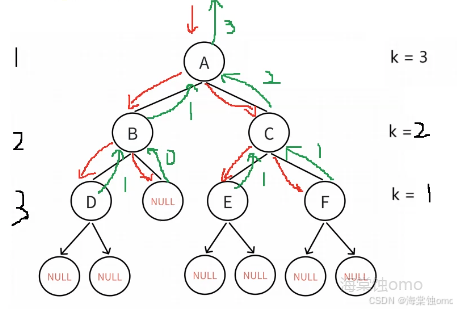
此方法的递归图，由图可以看出每次回溯返回的值为多少，最后将左子树和右子树回溯的值相加即可。

注意：每次递归传过去的值是k-1，不能是k，否则k的值不会改变。

int BinaryTreeHigh(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int left = BinaryTreeHigh(root->left);
	int right = BinaryTreeHigh(root->right);

	return 1 + (left > right ? left : right);
}

二叉树的高度/深度

此方法的思路：二叉树的高度=根结点的高度+左子树或右子树的高度，所以要判断左子树和右子树那边的高度更大。

通过这个思路我们就可以写出代码：

1.判断当前结点是否为NULL，是NULL就返回0

2.定义两个临时变量left和right，通过递归来记录左子树和右子树的高度

3.返回二叉树的高度

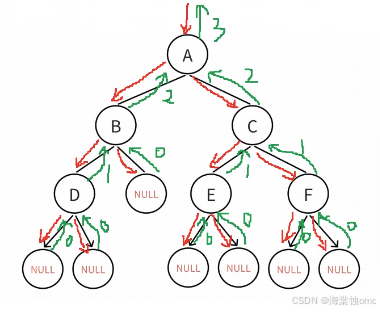
此方法的递归图，由此图我们可以看出左子树和右子树最终返回的高度是多少，再进行比较，如果左右子树高度相等，返回哪个都可以，最后和根结点的高度相加即可。

BTNode* BinaryTreeFind(BTNode* root, BTDateType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	//先递归左子树，看左子树有没有要找的点
	BTNode* left = BinaryTreeFind(root->left,x);
	if (left)
	{
		return left;
	}
	//再递归右子树，看右子树有没有要找的点
	BTNode* right = BinaryTreeFind(root->right,x);
	if (right)
	{
		return right;
	}
	//左右子树都没有找到，返回NULL
	return NULL;
}

查找二叉树中值为x的结点

此方法的思路：先在一边找，可以先从左子树找，也可以先从右子树找，如果在一边找到了，就不需要再递归另一边，找到了就返回该结点的地址即可，没找到就返回NULL。

根据这个思路我们可以写出代码： 1.判断当前结点是否为NULL，为NULL就返回NULL

2.不为NULL的情况下，判断结点内的数据是否是我们要找的数据，是的话直接返回地址

3.先递归左子树找有无符合条件的结点

4.左子树没有的情况下，递归右子树查找

5.都没有的情况下返回NULL

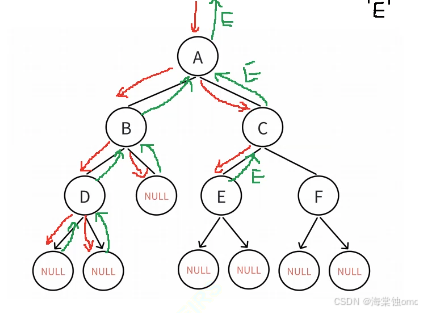
此方法的递归图，我们以查找'E'为例，进行递归查找，由图可知在左子树中并未找到相应结点，然后再递归右子树找到了相应结点，最后回溯返回结点地址即可。

void BinaryTreeDestory(BTNode** root)
{
	//后序遍历
	if (*root == NULL)
	{
		return;
	}
	BinaryTreeDestory(&((*root)->left));
	BinaryTreeDestory(&((*root)->right));
	free(*root);
	*root = NULL;
}

销毁二叉树

此方法思路：要用后序遍历来销毁结点，不能用前序遍历或者中序遍历，因为二者把根结点销毁之后就会找不到左右子树或右子树，而后序遍历就没有这种问题，最后再把根结点free掉即可。

通过此思路我们可以写出代码：

1.判断当前结点是否为NULL，是NULL就返回

2.通过递归先销毁左子树，再销毁右子树

3.最后销毁根结点

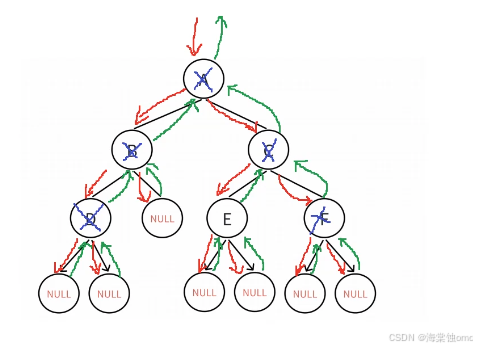
此方法的递归图，由图可以看出我们销毁二叉树是由下往上进行销毁的，这样就不会出现找不到左右子树的情况。

void LevelOrder(BTNode* root)
{
	QE q;
	QInit(&q);
	QPush(&q, root);
	while (!QEmpty(&q))
	{
		BTNode* top = QFront(&q);
		QPop(&q);
		printf("%c ", top->data);
		if (top->left)
		{
			QPush(&q, top->left);
		}
		if (top->right)
		{
			QPush(&q, top->right);
		}
	}

	QDestory(&q);
}

层序遍历

此方法思路：利用队列来实现，先把根结点放入队列中，然后把队头数据取出，打印出队头的数据，再把对头结点的左右孩子放入到队列中，放入左右孩子要先判断是否为NULL，不为NULL再放入队列中，重复上述循环，直到队列为空。

通过此思路我们可以写出代码：

1.创建队列，并初始化和销毁

2.把根结点放入队列中

3.通过循环把队头数据取出后，打印队头数据，再把队头的非空左右孩子放入队列中

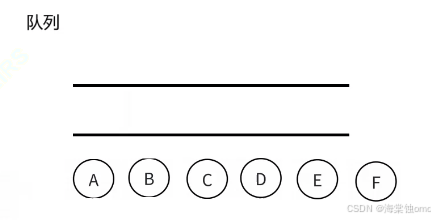
这就是最终取出的数据顺序，也就是层序遍历的结果。

bool IsBinaryCompleteTree(BTNode* root)
{
	QE q;
	QInit(&q);
	QPush(&q, root);
	while (!QEmpty(&q))
	{
		//取队头出对头
		BTNode* top = QFront(&q);
		QPop(&q);
		if (top == NULL)
		{
			break;
		}
		QPush(&q, top->left);
		QPush(&q, top->right);
	}
	//判断队列里的数据是否有非空结点
	while (!QEmpty(&q))
	{
		//取队头出对头
		BTNode* top = QFront(&q);
		QPop(&q);
		if (top != NULL)
		{
			QDestory(&q);
			return false;
		}
	}
	QDestory(&q);
	return true;
}

判断二叉树是否为完全二叉树

此方法思路：利用队列来实现，和层序遍历不同的是放入的左右孩子不需要判断是否为NULL，直接放入，当取出的数据为NULL时，循环停止，下面就要判断队列里面的内容，如果队列里没有非空结点，此二叉树就是完全二叉树，反之就不是完全二叉树。

通过此思路我们可以写出代码：

1.创建队列，并初始化和销毁

2.把根结点放入队列中

3.通过循环把队头数据取出后，打印队头数据，再把队头的非空左右孩子放入队列中

4.跳出循环代表取出的队头为NULL，再通过循环把队列里面的数据取出，如果队列里有非空结点，就直接返回false，代表不是完全二叉树

5.队列里的数据没有非空结点，返回true，代表是完全二叉树

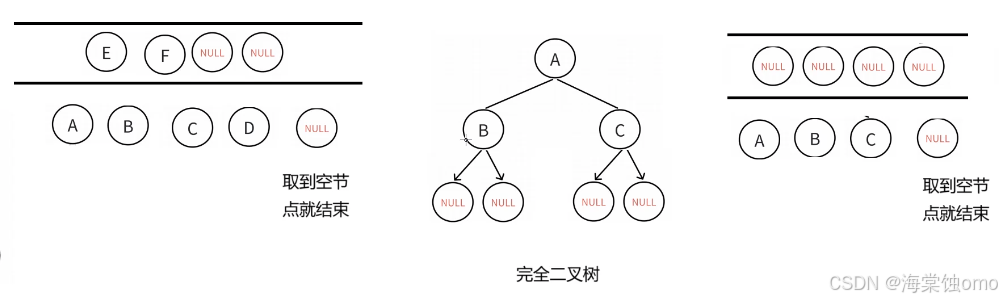
由图可知，左边为非完全二叉树第一次循环结束后队列里面的数据，右边是完全二叉树第一次循环结束后队列里面的数据，通过此方法我们就可以判断是否为完全二叉树。

1.3总结

二叉树的链式结构需要用到递归这种方式来实现，理解递归最好的方法就是画图，递归就是思路比较难想，但是想出来代码就很好实现。最后实现一个功能就检验一个功能，小编就是在检验层序遍历时发现了当初实现队列的一个错误。