【leetcode】《BFS扫荡术：如何用广度优搜索征服岛屿问题》
【leetcode】《BFS扫荡术：如何用广度优搜索征服岛屿问题》
——前言：小编本期将以基础的图像渲染为起点，展开讲解，其实几乎类似的问题都可以使用同一个模版，那么开始吧
📚️1.图像渲染
🚀1.1题目描述
有一幅以 m x n 的二维整数数组表示的图画 image ，其中 image[i][j] 表示该图画的像素值大小。你也被给予三个整数 sr , sc 和 color 。你应该从像素 image[sr][sc] 开始对图像进行上色 填充 。
为了完成 上色工作：
- 从初始像素开始，将其颜色改为
color。 - 对初始坐标的 上下左右四个方向上 相邻且与初始像素的原始颜色同色的像素点执行相同操作。
- 通过检查与初始像素的原始颜色相同的相邻像素并修改其颜色来继续 重复 此过程。
- 当 没有 其它原始颜色的相邻像素时 停止 操作。
最后返回经过上色渲染 修改 后的图像 。
大致就是如下所示：
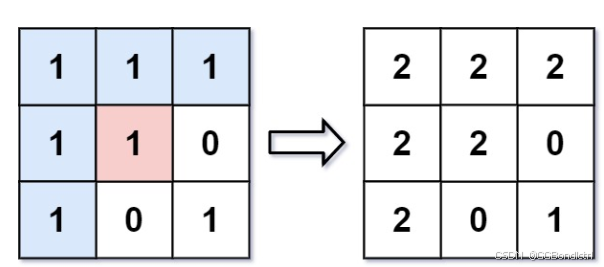
总结人话：
就是将其实目标位置的左右上下和自己一样的值以及包括自己的值变为新的值，并不断向外扩展；并且遇到0这种不一样的值，那么就不管即可；
🚀1.2题目分析
其实这里就已经很清楚了，我们使用BFS的思路就是：按照给定的位置进行向外扩展，（左右上下进行扩展），遇到0那么就直接不管，遇到1我们就进行修改；具体是如何进行扩展的呢？
1.我们首先创建一个队列以及将我们的初始位置进行记录入队
2.创建一个参照数组，判断此时这个位置是否已经被遍历过了
3.在循环中，出队列后按照这个位置进行左右上下的位置进行遍历判断
4.如果满足没有遍历以及位置上的值是1，那么就可以进行入队列
5.进入队列后，将此时的值进行修改，并且参照数组的对应位置的值也要改为已经遍历
具体的图示如下所示：
那么总结就是：
不断向外扩展，然后对于满足条件的位置进行入队列操作，不满足的位置那么就不管即可 ，在出队列后，按照出队列的位置进行上下左右的值的判断；
🚀1.3代码编写
具体的代码如下所示：
class Solution {
public int[][] floodFill(int[][] image, int sr, int sc, int color) {
int prve = image[sr][sc];
//创建一个向量数组
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
//创建一个队列
Queue<int[]> queue = new LinkedList<>();
if(image[sr][sc] == color){
return image;
}
//入队列中
queue.offer(new int[]{sr,sc});
while( !queue.isEmpty()){
int[] index = queue.poll();
int a = index[0];
int b = index[1];
image[a][b] = color;
//向量数组进行四周遍历操作
for(int i=0;i < 4;i++){
int x = a + dx[i];
int y = b + dy[i];
//边界情况
if( x >= 0 && x <image.length && y >=0 && y <image[0].length && image[x][y] == prve){
queue.offer(new int[]{x,y});
}
}
}
return image;
}
}解释：对于上下左右四个方向上的值，我们可以使用一个向量数组，来进行循环遍历四个位置；
注意：我们这里的队列保存的就是位置信息，如果不是位置信息，我们在出队列后，就不知道这个位置的上下左右四个位置信息了；
并且这里的判断是否能够进入队列的条件就是遍历的位置不能越界，并且位置上的值是目标值
注意：但是本题的标志位就是修改过后的新的值，所以这里不用设置我们的参照数组，小编主要是为了后面的题目~~~
📚️2.岛屿的数量
🚀2.1题目描述
给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外，你可以假设该网格的四条边均被水包围。
如下图就是：
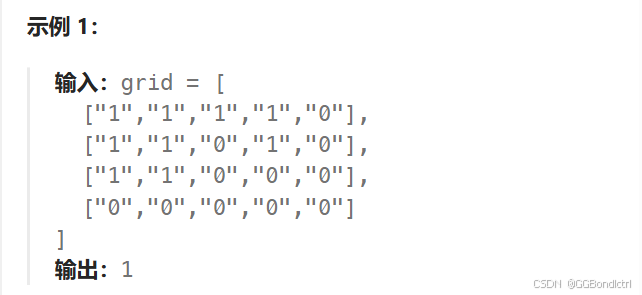
该题目如下所示：
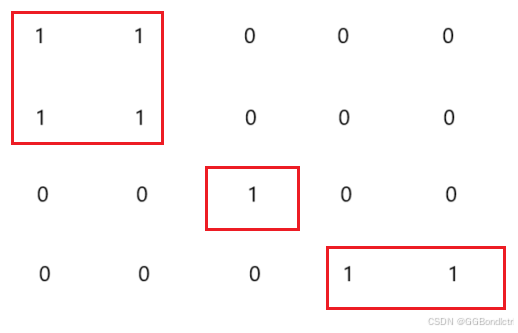
注意了：这里的连接是4连通，所以在对角线上的是不可以进行连接的；
🚀2.2题目分析
这里的思路就是就是非常清晰了，根据上面的题目来说；
具体过程思路如下：
我们还是创建一个队列来进行BFS，那么我们可以从第一个位置开始遍历，若为1，就以这个点为起始，然后向外扩展，然后完成后就是一个岛屿，那么此时我们的岛屿数量加1；并且（我们要设置一个参照数组）判断这个位置是否是已经被遍历了的~~~ 接下来我们继续遍历这个二维数组，然后当存在为1，并且没有被遍历的，那么就以这个为起始位置开始进行BFS来找到一个岛屿；循环往复
1.创建两层for循环，然后遍历我们的二维数组，并且创建一个参照二维数组，判断对应位置下的“岛屿”是否已经被遍历过的；
2.当我们的找到了岛屿一小部分就是“1”，并且我们没有遍历，那么就以这个位置进行BFS，将这个岛屿进行查找；
3.返回一个岛屿后进行结果加一的操作，然后继续循环遍历我们的二维数组，然后当遇到岛屿一小部分就是“1”，并且我们没有遍历，那么就直接进行BFS，循环往复；
🚀2.3代码编写
具体的代码如下所示：
class Solution {
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
boolean[][] vis = new boolean[301][301];
int result = 0;
int m;
int n;
public int numIslands(char[][] grid) {
m = grid.length;
n = grid[0].length;
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
//可以进行重复递归的条件
if(grid[i][j] == '1' && vis[i][j] == false){
result++;
bfs(grid,i,j);
}
}
}
return result;
}
public void bfs(char[][] grid,int i,int j){
//目的进行遍历，并将参照数组改为true
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{i,j});
vis[i][j] = true;
while(!queue.isEmpty()){
int[] index = queue.poll();
int a = index[0];
int b = index[1];
for(int k = 0;k < 4;k++){
int x = a + dx[k];
int y = b + dy[k];
if(x >= 0 && x < m && y >=0 && y <n && grid[x][y] == '1' && vis[x][y] == false){
queue.add(new int[]{x,y});
vis[x][y] = true;
}
}
}
}
}注意：
这里的判断是否进行入队列的条件，并且在入队列后，将我们的参照数组对应位置的值改为true，其实可以发现在BFS的核心代码和上面的图像渲染几乎是一致的，所以BFS核心代码就是一个模版直接套入就行~~~
📚️3.被围绕的区域
🚀3.1题目描述
给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' 组成，捕获 所有 被围绕的区域：
- 连接：一个单元格与水平或垂直方向上相邻的单元格连接。
- 区域：连接所有
'O'的单元格来形成一个区域。 - 围绕：如果您可以用
'X'单元格 连接这个区域，并且区域中没有任何单元格位于board边缘，则该区域被'X'单元格围绕。
通过 原地 将输入矩阵中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。你不需要返回任何值
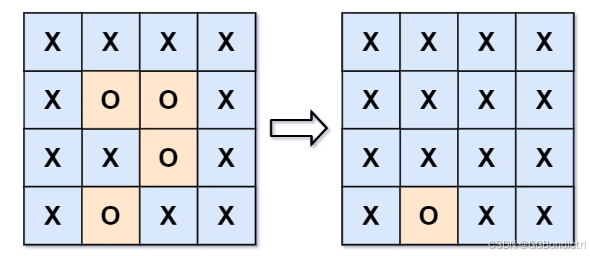
总结成人话就是：
我们要将为‘O’变成‘X’，并且这个‘O’的变成‘X’的位置不可以在整个二维数组的边缘~~~
🚀3.2题目分析
经过上面的几道题分析，可以知道关于岛屿问题就是使用BFS进行操作；但是我们如何解决边缘位置的‘O’问题呢？其实哦们可以反之来，即遍历我们的边缘，然后只要与边缘连接的岛屿就是我们不必修改的，所以就可以使用BFS来解决
步骤：
1.遍历我们的边缘位置，找到我们的为‘O’的区域，并且这个区域没有被遍历 2.使用BFS算法进行区域遍历，将遍历的值进行修改为一个特殊符号 3.循环完之后，再次遍历整个二维数组，将遇到的内部‘O’修改为‘X’，然后遍历到我们的特殊字符（就是没有被包围的区域）修改为‘O’即可~~~
🚀 3.3代码编写
代码如下所示：
class Solution {
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
boolean[][] vis = new boolean[201][201];
int m;
int n;
public void solve(char[][] board) {
m = board.length;
n = board[0].length;
//遍历边界
for(int i = 0; i < m ; i++){
for(int j = 0; j < n; j++){
//判断是否是边界，若不是就跳过此次循环
if( i > 0 && i < (m - 1)){
if( j > 0 && j < (n - 1)){
continue;
}
}
//正常遍历
if(board[i][j] == 'O' && vis[i][j] == false){
bfs(board,i,j);
}
}
}
//最后遍历数组修改数据
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j ++){
if(board[i][j] == 'O'){
board[i][j] = 'X';
}else if(board[i][j] == '.'){
board[i][j] = 'O';
}
}
}
}
public void bfs(char[][] board,int i,int j){
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{i,j});
vis[i][j] = true;
board[i][j] = '.';
while(!queue.isEmpty()){
int[] index = queue.poll();
int a = index[0];
int b = index[1];
for(int k = 0; k < 4; k++){
int x = a + dx[k];
int y = b + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O' && vis[x][y] == false){
queue.add(new int[]{x,y});
board[x][y] = '.';
vis[x][y] = true;
}
}
}
}
}所以可以看到我们对于BFS遍历区域的反复使用，只不过要根据不同的情况来进行特殊处理；
注意我们如何进行边缘的遍历，以及BFS编写模版即可~~~
📚️4.总结
本期主要讲解了力扣上，几道关于我们的BFS遍历的岛屿问题~~~
🌅🌅🌅~~~~最后希望与诸君共勉，共同进步！！！
腾讯云开发者
