ScholarCopilot:智能学术写作革命,告别引用焦虑
ScholarCopilot:智能学术写作革命,告别引用焦虑

CoderJia
发布于 2025-04-14 09:17:37
发布于 2025-04-14 09:17:37
在学术研究的征途中,论文写作无疑是关键一环,而准确、规范的引用更是衡量学术严谨性的重要标尺。然而,繁琐的文献检索、格式调整以及在写作过程中实时插入恰当引用的需求,常常让研究者们倍感压力。今天,我们将深入探讨一个旨在革新这一流程的开源项目——ScholarCopilot,一个由 TIGER-Lab 倾力打造的智能学术写作助手。它不仅仅是一个简单的文本生成工具,更是一位懂得何时、何地、如何精准引用的“学术副驾驶”。

ScholarCopilot项目主页
引言:学术写作的痛点与 AI 的曙光
撰写高质量的学术论文,不仅需要清晰的逻辑、深入的见解,还需要对相关文献的广泛涉猎和精确引用。传统的写作流程中,研究者往往需要在不同的工具和数据库之间切换,手动查找、筛选、整理文献,并按照特定的格式插入文中,这一过程耗时耗力且容易出错。近年来,大型语言模型(LLM)在文本生成方面取得了显著进展,但将其直接应用于需要高度精确性和严谨性的学术写作,尤其是在处理引文方面,仍然面临巨大挑战。通用 LLM 往往难以保证引用的真实性和准确性,甚至可能产生“幻觉”引用。
正是在这样的背景下,ScholarCopilot 应运而生。它并非简单地替换写作者,而是作为一个强大的“Copilot”,在写作过程中提供智能化的辅助,特别是在文本补全和引用管理这两个核心环节上,展现出了令人瞩目的能力。
ScholarCopilot 的核心武器库:智能生成与精准引用
ScholarCopilot 的核心价值在于其两大关键特性:智能化的文本生成和精准的引用管理。这不仅仅是功能的堆砌,而是基于对学术写作流程深刻理解的精心设计。
智能文本生成:不止于“下一句”
许多写作助手都能提供文本建议,但 ScholarCopilot 的目标是提供更贴合学术语境的、结构化的内容生成。
- 上下文感知的句子建议: 它不仅仅是预测下一个词,而是能根据你已经写下的内容,提供接下来三句高度相关的、符合学术表达习惯的句子建议。这有助于打破写作障碍,保持思路流畅。
- 完整章节的自动补全: 对于论文中的标准章节(如引言、相关工作、方法等),ScholarCopilot 能够根据上下文和用户的初步输入,生成结构完整、逻辑连贯的章节草稿。这极大地提高了初稿的撰写效率。
- 保持连贯性: 所有的文本生成都基于对现有文本的理解,确保新生成的内容与前文在风格、术语和逻辑上保持一致,避免了通用模型可能产生的突兀感。
智能引用管理:让引用恰到好处
这是 ScholarCopilot 最具特色的功能,也是其区别于许多通用写作工具的关键所在。
- 实时上下文引用建议: 在你写作时,ScholarCopilot 会实时分析文本内容,并在它认为需要引用支撑的地方,主动推荐相关的参考文献。这就像有一位经验丰富的导师在旁边提醒你:“这里需要一个引用来支持你的观点。”
- 一键式引用插入: 对于推荐的文献,用户只需简单点击,即可将其按照规范的学术格式(如 [1], (Author, Year) 等,具体格式可能需配置)插入到当前光标位置。
- BibTeX 条目自动生成与导出: 更为便捷的是,所有插入的引用,ScholarCopilot 都能自动生成对应的 BibTeX 条目,方便用户在论文末尾整理参考文献列表,并导出使用。
揭秘背后机制:检索与生成的动态协同
如此智能的功能是如何实现的?ScholarCopilot 的 README 文件揭示了其核心的推理流程:一个巧妙融合了检索(Retrieval)与生成(Generation)的统一模型架构。
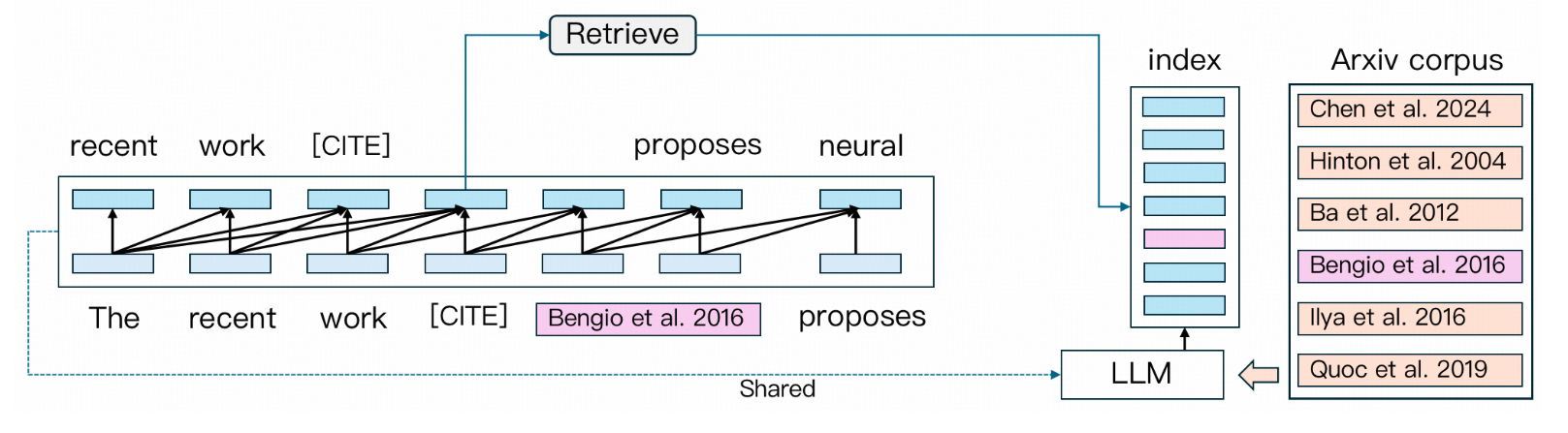
Inference Pipeline Overview
(图片来源: ScholarCopilot GitHub Repository)
这个流程的关键在于一种动态切换机制。模型在生成文本的过程中,并非一味地向前输出,而是会利用其学习到的“引用模式”(learned citation patterns)来判断当前位置是否适合插入引用。
当模型判定需要引用时,它会暂停文本生成任务,并利用生成到“引用标记”(citation token)时的隐藏状态(hidden states)。这些隐藏状态编码了当前上下文的语义信息,可以被视为一个高效的查询向量。模型使用这个向量在其内部或外部的论文语料库(Corpus)中进行检索,找到最相关的几篇论文。
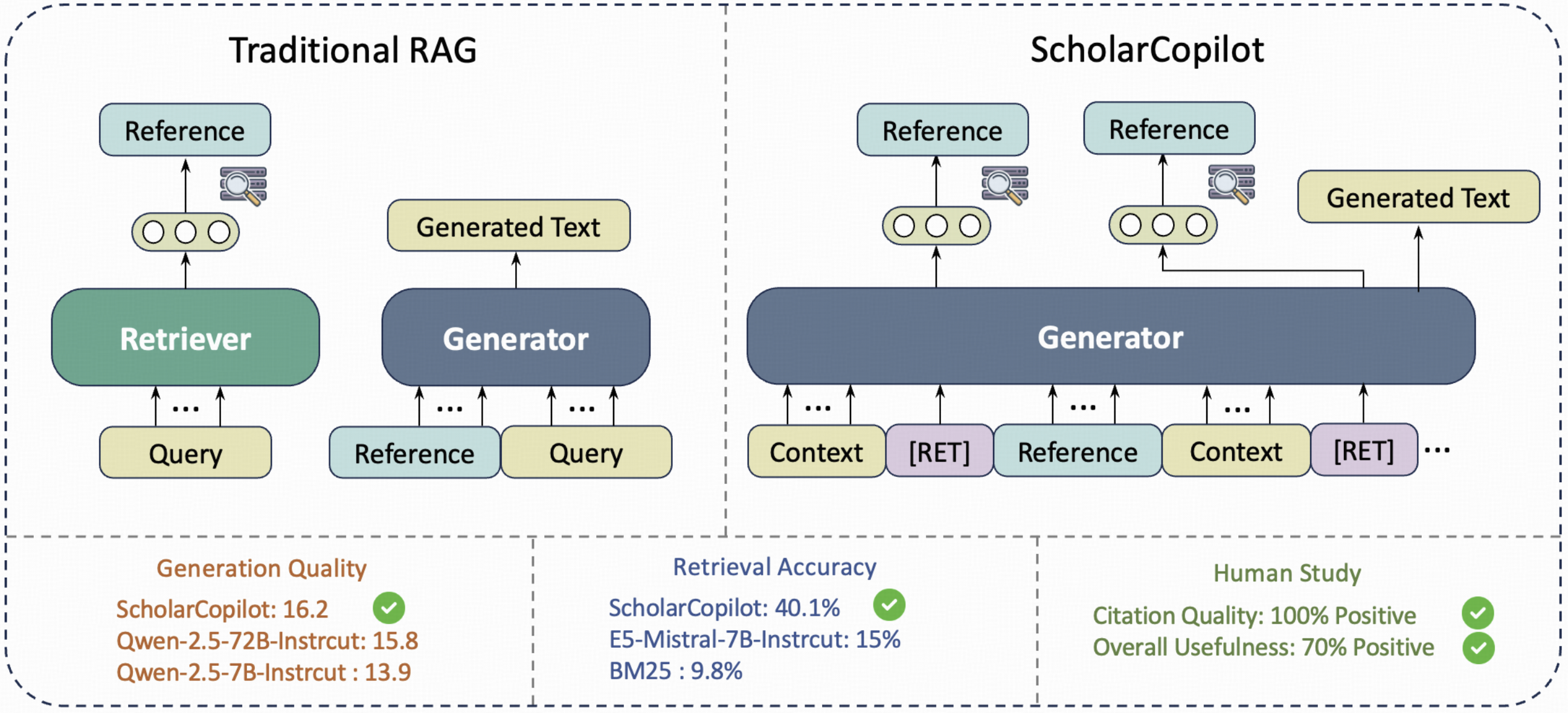
teaser
一旦用户确认或模型选择了合适的参考文献,系统会将其格式化并插入文本。随后,模型会无缝地切换回生成模式,基于更新后的上下文继续撰写连贯的文本。这种“生成-判断-检索-插入-继续生成”的闭环,使得 ScholarCopilot 能够将精准的引用有机地融入流畅的写作过程中,这相较于传统的“先写后补”或依赖外部插件的引用方式,无疑是巨大的进步。
快速上手:部署与使用你的 ScholarCopilot
TIGER-Lab 不仅发布了研究成果,还提供了代码和 Demo,让开发者和研究者能够快速体验和部署。
部署本地 Demo:
克隆仓库:
git clone git@github.com:TIGER-AI-Lab/ScholarCopilot.git
cd ScholarCopilot/run_demo设置环境:
pip install -r requirements.txt下载模型与数据: 项目提供了便捷的脚本来下载所需资源。
bash download.sh启动 Demo:
bash run_demo.sh执行完毕后,根据提示即可在本地访问 ScholarCopilot 的演示界面。
保持语料库更新:
学术研究日新月异,保持引用语料库的更新至关重要。ScholarCopilot 也考虑到了这一点,提供了更新 arXiv 语料库的流程:
从 Kaggle 等渠道下载最新的 arXiv 元数据。
使用提供的 Python 脚本处理元数据:
cd utils/
python process_arxiv_meta_data.py ARXIV_META_DATA_PATH ../data/corpus_data_arxiv_1215.jsonl为新的语料库生成嵌入(Embedding),这是后续高效检索的基础:
bash encode_corpus.sh构建 HNSW(Hierarchical Navigable Small World)索引,以实现快速相似性搜索:
python build_hnsw_index.py --input_dir <embedding dir> --output_dir <hnsw index dir>通过这些步骤,你可以将最新的研究成果纳入 ScholarCopilot 的“视野”。
(可选) 训练专属模型:
对于有更高定制化需求或希望在特定领域语料上进行优化的用户,项目还提供了训练指南:
- 下载训练数据:
cd train/ && bash download.sh - 配置并运行训练脚本:
cd src/ && bash start_train.sh- 注意:根据文档,复现论文结果需要相当大的计算资源(例如 4 台机器,每台 8 个 GPU,共 32 个 GPU)。
应用前景
ScholarCopilot 的出现,为广大学生、教师和科研工作者带来了福音。
- 效率提升: 大幅缩短文献检索、引用格式调整和文本撰写的时间,让研究者能更专注于思考和创新。
- 质量保障: 智能推荐和一键插入有助于减少引用错误和遗漏,提高论文的规范性和严谨性。
- 降低门槛: 对于初涉科研的学生,它能作为一个很好的辅助工具,帮助他们更快地掌握学术写作规范。
相较于市面上其他写作工具或通用大模型,ScholarCopilot 的核心优势在于其深度整合的、上下文感知的、以精准引用为目标的设计理念。它不是简单地做文本生成或文献管理,而是将两者无缝结合,真正服务于学术写作的特殊需求。
当然,作为一项新兴技术,它也可能存在一些局限性,例如对特定领域、非英语文献的覆盖程度,对复杂引用格式的适应性,以及对计算资源的需求等。但其展现出的潜力已足够令人兴奋。
结论
ScholarCopilot 以其创新的思路和实用的功能,为我们描绘了 AI 赋能学术写作的美好图景。它通过智能化的文本生成和精准的引用管理,有望将研究者从繁琐的事务性工作中解放出来,显著提升科研产出的效率和质量。虽然项目仍在发展中,但其开源的模式、清晰的架构和详尽的指南,无疑为社区的进一步贡献和完善奠定了良好基础。
如果你也为学术写作中的引用问题所困扰,不妨关注并尝试一下 ScholarCopilot。它或许就是你一直在寻找的那个“学术副驾驶”。
资源链接:
- 项目主页: https://tiger-ai-lab.github.io/ScholarCopilot/
- 论文: https://arxiv.org/abs/2504.00824
- 数据: https://huggingface.co/datasets/TIGER-Lab/ScholarCopilot-Data-v1/
- 模型: https://huggingface.co/TIGER-Lab/ScholarCopilot-v1
- Demo: https://huggingface.co/spaces/TIGER-Lab/ScholarCopilot
- GitHub: https://github.com/TIGER-AI-Lab/ScholarCopilot (注:实际链接根据项目情况确定,此处为推测)
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-04-13,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

