《信号与系统》第一章信号与系统

啊阿狸不会拉杆

发布于 2026-01-21 11:49:28

1300

1.1 绪论

信号与系统是研究信号在系统中传输与处理的基本理论，广泛应用于通信、控制、信号处理等领域。本章将介绍信号与系统的基本概念、分类、运算及系统特性分析。

1.2 信号

一、连续信号和离散信号

连续信号：在连续时间范围内有定义的信号，通常用 x (t) 表示。

离散信号：仅在离散时间点上有定义的信号，通常用 x [n] 表示。

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 1. 绘制连续时间正弦信号
t = np.linspace(0, 2*np.pi, 1000)  # 连续时间点
x_continuous = np.sin(t)  # 连续正弦信号

plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(t, x_continuous)
plt.title("连续时间正弦信号")
plt.xlabel("时间 t")
plt.ylabel("幅度")
plt.grid(True)

# 2. 绘制离散时间正弦序列
n = np.arange(0, 20)  # 离散时间点
x_discrete = np.sin(0.2 * np.pi * n)  # 离散正弦序列

plt.subplot(1, 2, 2)
# 使用关键字参数设置样式
plt.stem(n, x_discrete, markerfmt='ro', linefmt='r-', basefmt='r--')
plt.title("离散时间正弦序列")
plt.xlabel("时间 n")
plt.ylabel("幅度")
plt.grid(True)
plt.tight_layout()
plt.show()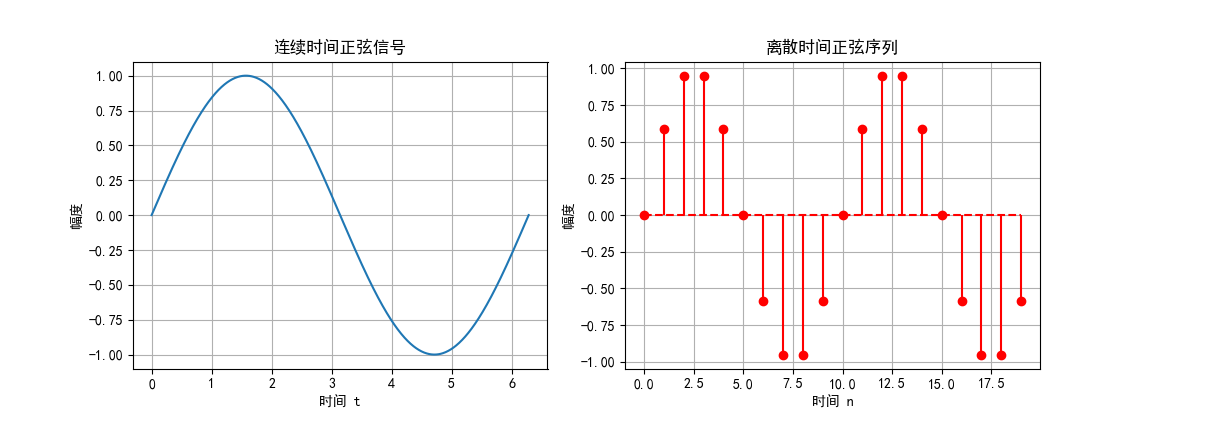

图 1：连续信号与离散信号示例

二、周期信号和非周期信号

周期信号：满足 x (t+T) = x (t) 或 x [n+N] = x [n] 的信号，T 和 N 为周期。

非周期信号：不满足周期性的信号。

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 周期信号与非周期信号示例
t = np.linspace(0, 4*np.pi, 1000)
x_periodic = np.sin(t) + 0.5*np.sin(2*t)  # 周期信号（基波周期2π）

# 非周期信号：指数衰减信号
x_aperiodic = np.exp(-0.5*t) * np.sin(t)

plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(t, x_periodic)
plt.title("周期信号（正弦叠加）")
plt.xlabel("时间 t")
plt.ylabel("幅度")
plt.grid(True)

plt.subplot(1, 2, 2)
plt.plot(t, x_aperiodic)
plt.title("非周期信号（指数衰减正弦）")
plt.xlabel("时间 t")
plt.ylabel("幅度")
plt.grid(True)
plt.tight_layout()
plt.show()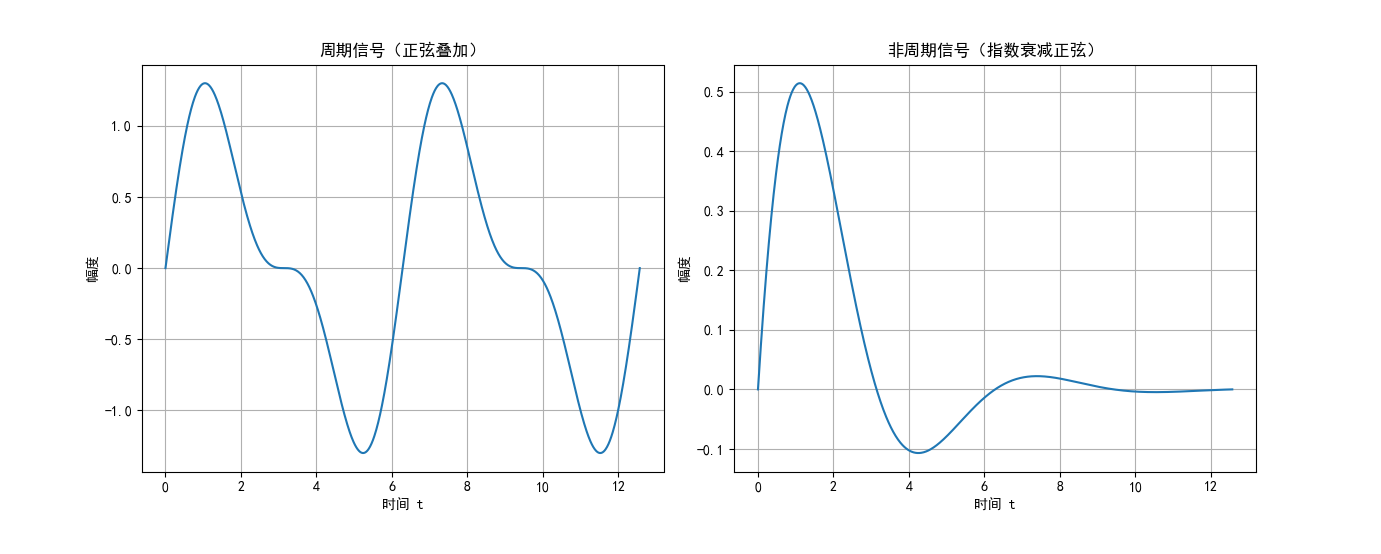

图 2：周期信号与非周期信号示例

三、实信号和复信号

实信号：幅度为实数的信号，如 x (t) ∈ ℝ。

复信号：幅度为复数的信号，通常表示为 x (t) = a (t) + jb (t)，其中 j 为虚数单位。

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 复信号示例：复指数信号
t = np.linspace(0, 2*np.pi, 1000)
# 复指数信号：e^(jωt) = cos(ωt) + j*sin(ωt)
omega = 1  # 角频率
x_complex = np.exp(1j * omega * t)  # 复指数信号

# 提取实部和虚部
real_part = np.real(x_complex)
imag_part = np.imag(x_complex)

plt.figure(figsize=(10, 6))
plt.plot(t, real_part, 'b-', label='实部 cos(ωt)')
plt.plot(t, imag_part, 'r--', label='虚部 sin(ωt)')
plt.title("复指数信号 e^(jωt) 的实部与虚部")
plt.xlabel("时间 t")
plt.ylabel("幅度")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()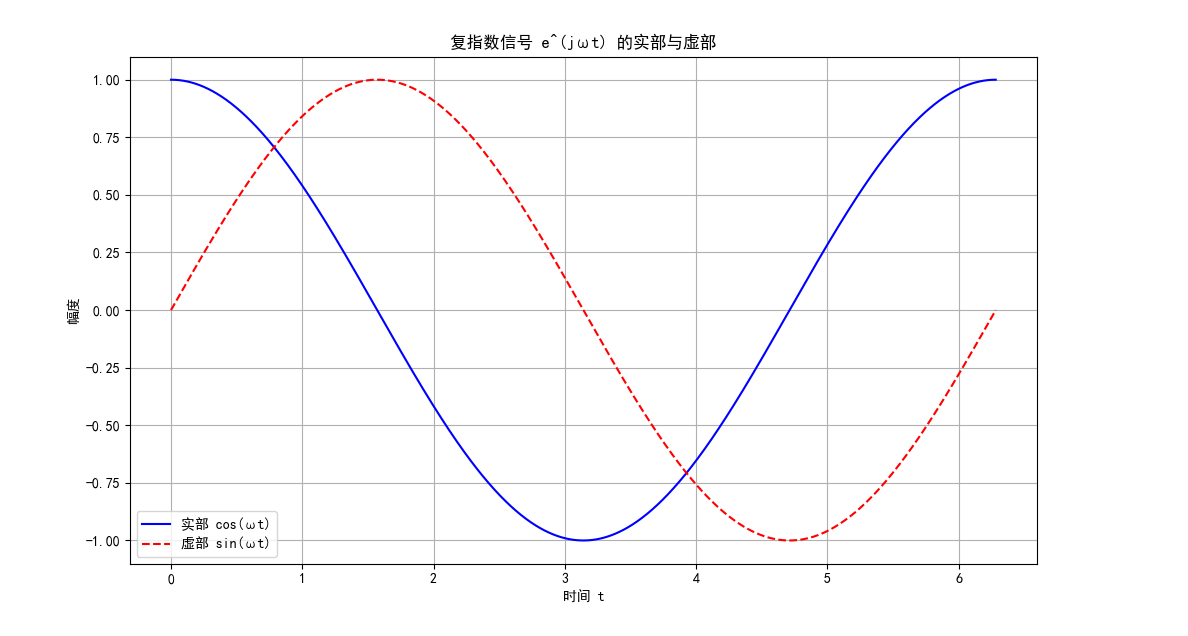

图 3：复指数信号的实部与虚部

四、能量信号和功率信号

import matplotlib.pyplot as plt
import numpy as np


plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 能量信号与功率信号示例
t = np.linspace(-5, 5, 1000)

# 能量信号：矩形脉冲
x_energy = np.zeros_like(t)
x_energy[(t >= -1) & (t <= 1)] = 1  # 宽度为2的矩形脉冲

# 功率信号：正弦波（周期信号）
x_power = np.sin(2*np.pi*t)

plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(t, x_energy)
plt.title("能量信号（矩形脉冲）")
plt.xlabel("时间 t")
plt.ylabel("幅度")
plt.grid(True)

plt.subplot(1, 2, 2)
plt.plot(t, x_power)
plt.title("功率信号（正弦波）")
plt.xlabel("时间 t")
plt.ylabel("幅度")
plt.grid(True)
plt.tight_layout()
plt.show()

# 计算能量与功率（近似）
def calculate_energy(x, dt):
    """计算信号能量"""
    return np.sum(np.abs(x)**2) * dt

def calculate_power(x, dt, T):
    """计算信号功率（在时间区间[-T,T]内的平均功率）"""
    return calculate_energy(x, dt) / (2*T)

dt = t[1] - t[0]
T = 5  # 计算功率的时间区间

energy_rect = calculate_energy(x_energy, dt)
power_sin = calculate_power(x_power, dt, T)

print(f"矩形脉冲能量：{energy_rect:.4f}")
print(f"正弦波功率：{power_sin:.4f}")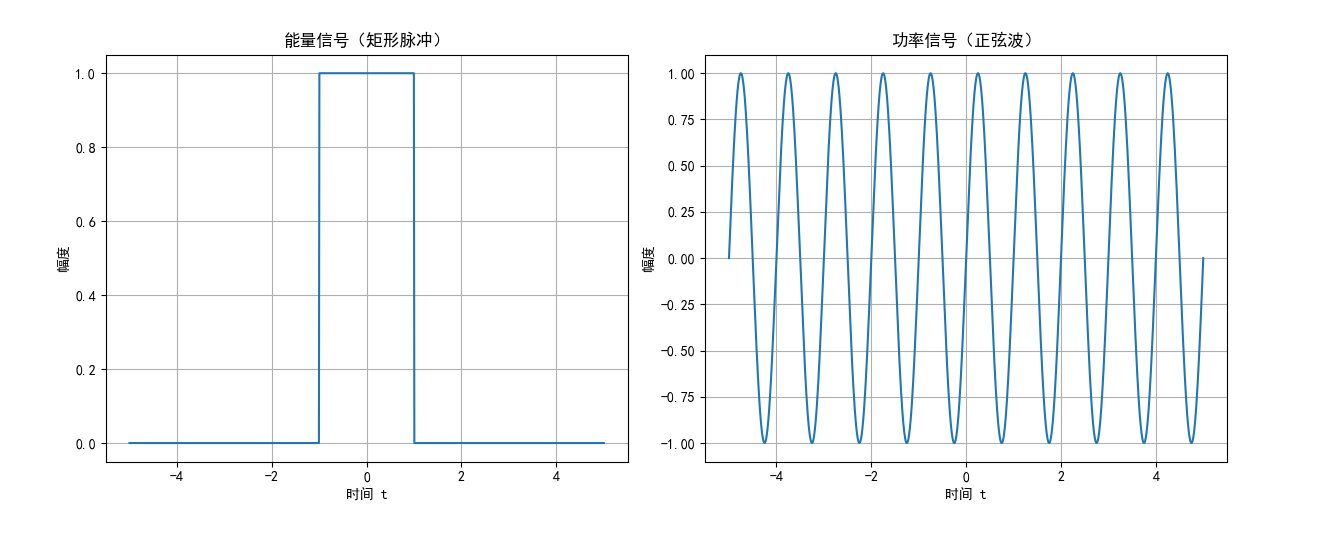

图 4：能量信号与功率信号示例 代码输出：矩形脉冲能量约为 2.0，正弦波功率约为 0.5（理论值）

1.3 信号的基本运算

一、加法和乘法

信号加法：(x1 + x2)(t) = x1 (t) + x2 (t)

信号乘法：(x1・x2)(t) = x1 (t)・x2 (t)

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

t = np.linspace(0, 2*np.pi, 1000)
x1 = np.sin(t)
x2 = np.sin(2*t)

# 信号加法
x_sum = x1 + x2
# 信号乘法
x_product = x1 * x2

plt.figure(figsize=(12, 6))
plt.subplot(2, 2, 1)
plt.plot(t, x1, 'b-', label='x1(t)=sin(t)')
plt.title("信号x1(t)")
plt.xlabel("时间 t")
plt.legend()
plt.grid(True)

plt.subplot(2, 2, 2)
plt.plot(t, x2, 'r-', label='x2(t)=sin(2t)')
plt.title("信号x2(t)")
plt.xlabel("时间 t")
plt.legend()
plt.grid(True)

plt.subplot(2, 2, 3)
plt.plot(t, x_sum, 'g-', label='x1+x2')
plt.title("信号加法")
plt.xlabel("时间 t")
plt.legend()
plt.grid(True)

plt.subplot(2, 2, 4)
plt.plot(t, x_product, 'm-', label='x1·x2')
plt.title("信号乘法")
plt.xlabel("时间 t")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()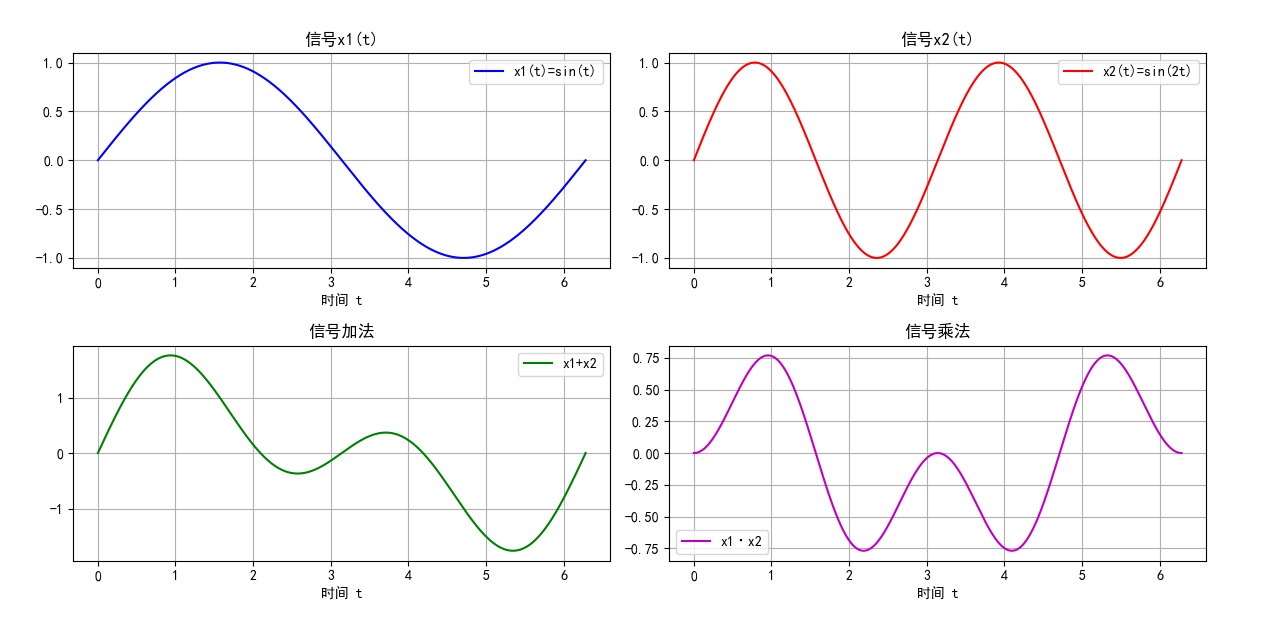

图 5：信号的加法与乘法运算

二、反转和平移

反转：x (-t) 或 x [-n]，信号沿时间轴翻转。

平移：x (t-t0) 或 x [n-n0]，信号沿时间轴平移 t0 或 n0。

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
t = np.linspace(-5, 5, 1000)
# 原始信号：高斯函数
x = np.exp(-0.5 * (t/2)**2)

# 反转信号
x_reversed = x[::-1]
# 平移信号（t0=2）
x_shifted = np.roll(x, int(2 / (t[1]-t[0])))  # 平移2个单位

plt.figure(figsize=(12, 5))
plt.subplot(1, 3, 1)
plt.plot(t, x)
plt.title("原始信号")
plt.xlabel("时间 t")
plt.grid(True)

plt.subplot(1, 3, 2)
plt.plot(t, x_reversed)
plt.title("反转信号 x(-t)")
plt.xlabel("时间 t")
plt.grid(True)

plt.subplot(1, 3, 3)
plt.plot(t, x_shifted)
plt.title(f"平移信号 x(t-{2})")
plt.xlabel("时间 t")
plt.grid(True)
plt.tight_layout()
plt.show()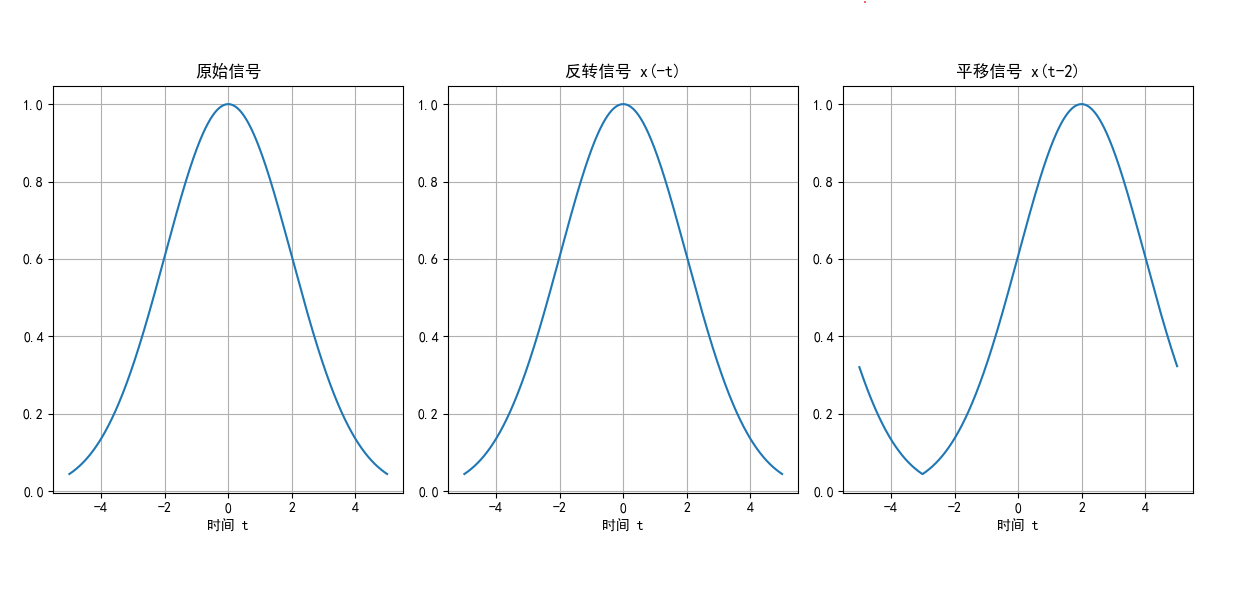

图 6：信号的反转与平移运算

三、尺度变换（横坐标展缩）

尺度变换：x (at)，a>1 时信号压缩，0<a<1 时信号扩展。

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

t = np.linspace(-5, 5, 1000)
x = np.exp(-0.5 * t**2)  # 高斯函数

# 尺度变换：a=2（压缩）和 a=0.5（扩展）
x_compressed = x[::2]  # 压缩，a=2
t_compressed = t[::2]

x_expanded = np.interp(np.linspace(-5, 5, 2000), t, x)  # 扩展，a=0.5
t_expanded = np.linspace(-5, 5, 2000)

plt.figure(figsize=(12, 5))
plt.subplot(1, 3, 1)
plt.plot(t, x)
plt.title("原始信号 x(t)")
plt.xlabel("时间 t")
plt.grid(True)

plt.subplot(1, 3, 2)
plt.plot(t_compressed, x_compressed)
plt.title("压缩信号 x(2t)")
plt.xlabel("时间 t")
plt.grid(True)

plt.subplot(1, 3, 3)
plt.plot(t_expanded, x_expanded)
plt.title("扩展信号 x(0.5t)")
plt.xlabel("时间 t")
plt.grid(True)
plt.tight_layout()
plt.show()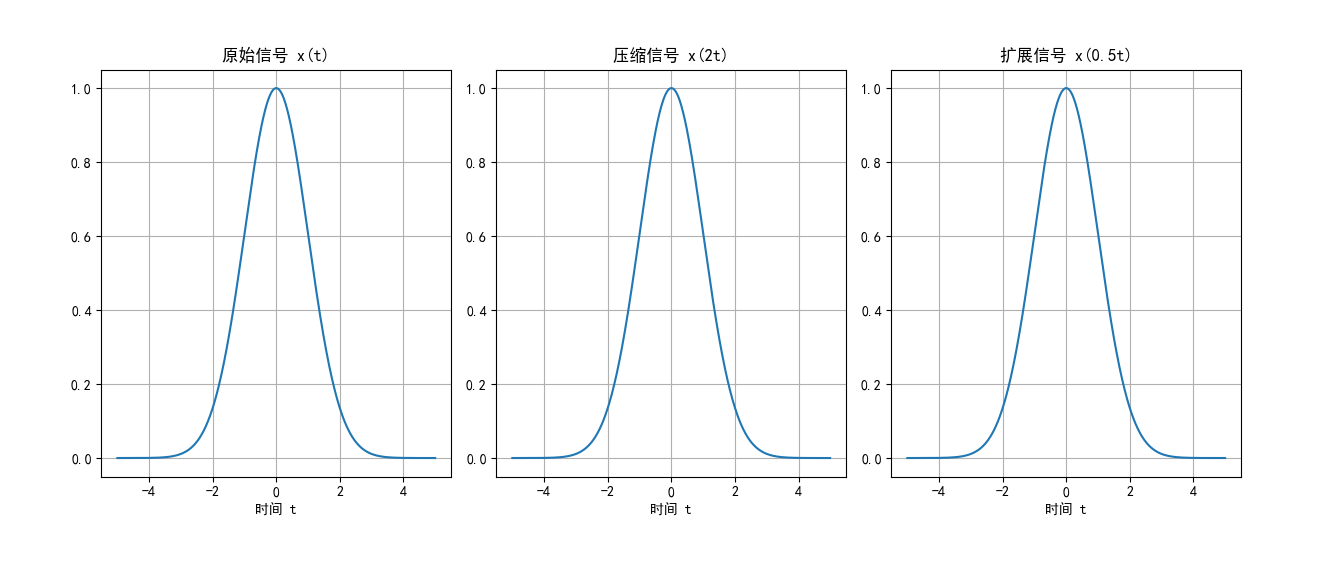

图 7：信号的尺度变换运算

1.4 阶跃函数和冲激函数

一、阶跃函数和冲激函数

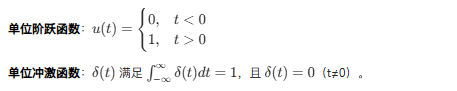
import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

t = np.linspace(-5, 5, 1000)
dt = t[1] - t[0]

# 单位阶跃函数（使用numpy的heaviside函数）
u = np.heaviside(t, 0.5)  # t=0时定义为0.5

# 单位冲激函数（近似为窄脉冲）
delta = np.zeros_like(t)
delta[np.abs(t) < 0.01] = 1/(0.02)  # 宽度0.02，面积为1

plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(t, u)
plt.step(t, u, where='post', color='b', alpha=0.7)
plt.title("单位阶跃函数 u(t)")
plt.xlabel("时间 t")
plt.ylabel("幅度")
plt.grid(True)

plt.subplot(1, 2, 2)
plt.plot(t, delta)
plt.title("单位冲激函数 δ(t)（近似）")
plt.xlabel("时间 t")
plt.ylabel("幅度")
plt.grid(True)
plt.tight_layout()
plt.show()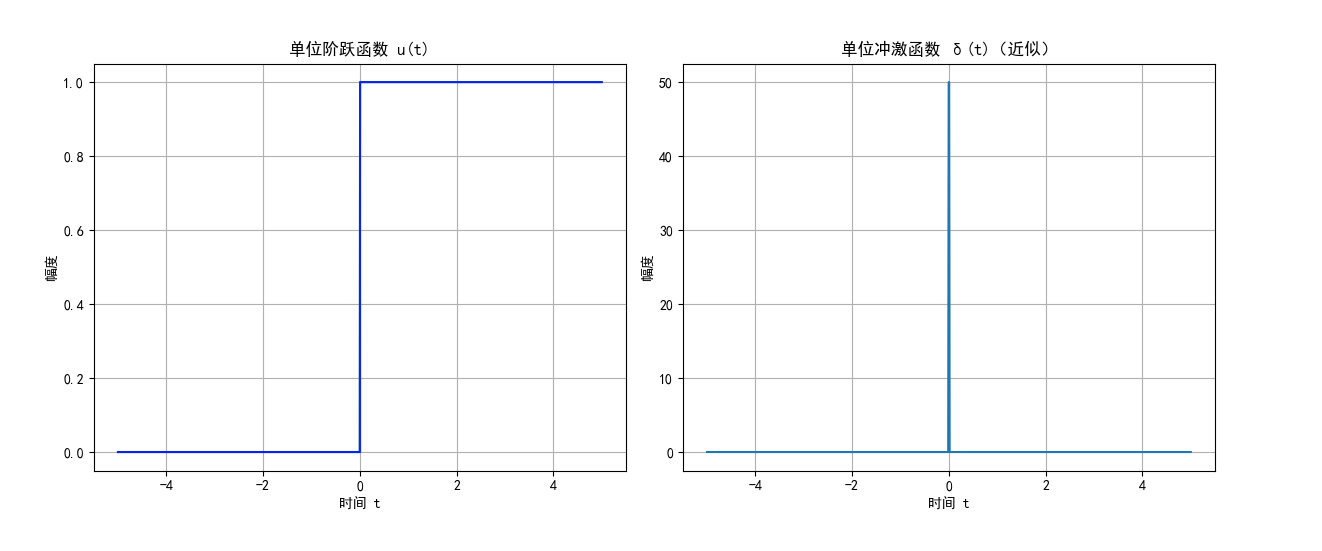

图 8：单位阶跃函数与单位冲激函数

二、冲激函数的广义函数定义

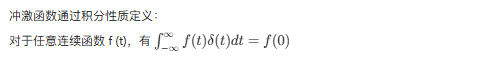
三、冲激函数的导数和积分

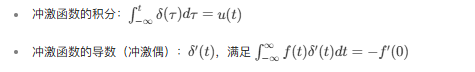
四、冲激函数的性质

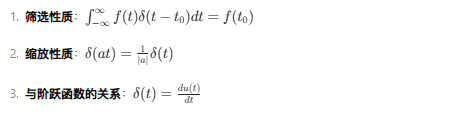
import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 冲激函数筛选性质示例
t = np.linspace(-5, 5, 1000)
dt = t[1] - t[0]

# 任意连续函数 f(t) = t^2 * exp(-0.5t^2)
f = t**2 * np.exp(-0.5 * t**2)

# 冲激函数 δ(t-1)（近似）
delta = np.zeros_like(t)
delta[np.abs(t-1) < 0.01] = 1/(0.02)  # 在t=1处的冲激

# 计算 f(t)δ(t-1) 的积分（筛选性质）
integral = np.sum(f * delta) * dt
理论值 = (1)**2 * np.exp(-0.5 * (1)** 2)  # f(1)

plt.figure(figsize=(10, 6))
plt.plot(t, f, 'b-', label='f(t)')
plt.plot(t, delta*5, 'r-', label='δ(t-1)（缩放5倍显示）')
plt.plot(t, f*delta*5, 'g-', label='f(t)δ(t-1)（缩放5倍显示）')
plt.title(f"冲激函数筛选性质：∫f(t)δ(t-1)dt = {integral:.4f} ≈ f(1)={理论值:.4f}")
plt.xlabel("时间 t")
plt.ylabel("幅度")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()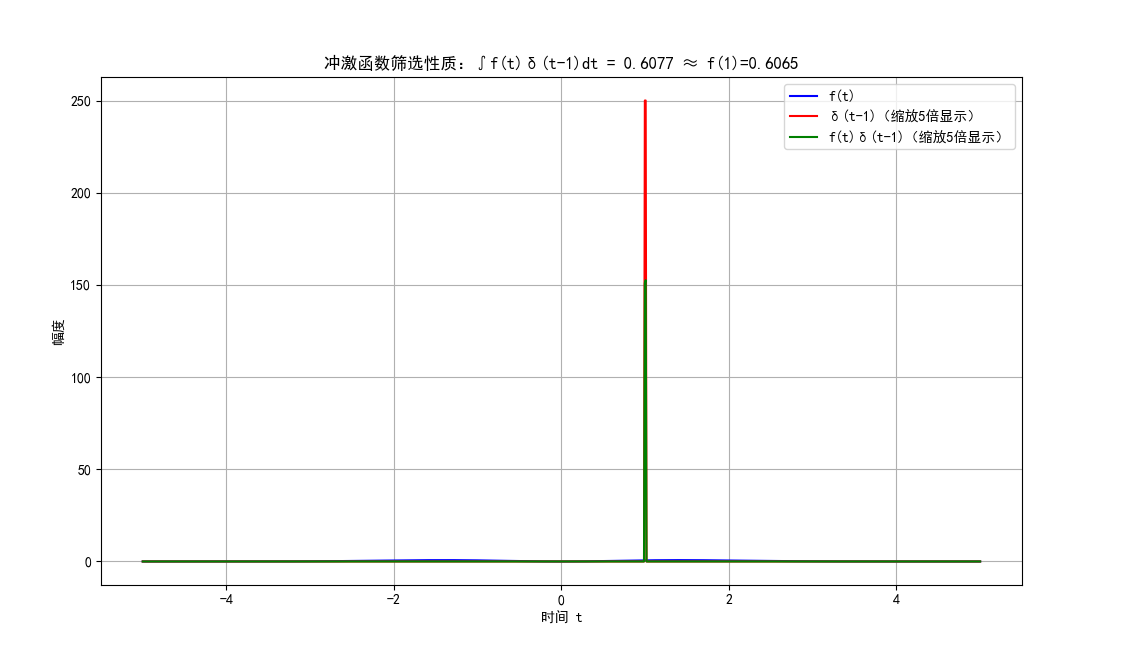

图 9：冲激函数的筛选性质示例

1.5 系统的描述

一、系统的数学模型

二、系统的框图表示

系统框图由基本单元（加法器、乘法器、积分器 / 延迟器）组成。

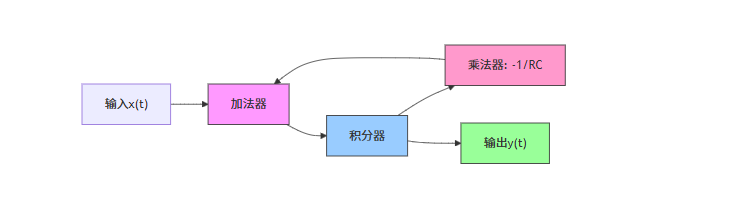
图 10：RC 低通滤波器的框图表示

1.6 系统的特性和分析方法

一、线性

线性系统满足叠加性和齐次性：

叠加性：T （x1 (t)+x2 (t)）= T （x1 (t)） + T （x2 (t)）
齐次性：T (kx (t)) = kT (x (t))

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 线性系统验证示例：系统y(t) = 2x(t) + 1（非线性）与 y(t)=3x(t)（线性）

def system1(x):
    """非线性系统：y=2x+1"""
    return 2*x + 1

def system2(x):
    """线性系统：y=3x"""
    return 3*x

t = np.linspace(0, 5, 100)
x1 = np.sin(t)
x2 = np.cos(t)

# 验证叠加性
y1 = system1(x1)
y2 = system1(x2)
y_sum = system1(x1 + x2)
y1_plus_y2 = y1 + y2

# 验证齐次性
k = 2
y_scaled = system1(k*x1)
k_times_y1 = k*y1

plt.figure(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.plot(t, y_sum, 'r-', label='y(x1+x2)')
plt.plot(t, y1_plus_y2, 'b--', label='y(x1)+y(x2)')
plt.title("非线性系统叠加性验证")
plt.xlabel("时间 t")
plt.legend()
plt.grid(True)

plt.subplot(2, 2, 2)
plt.plot(t, y_scaled, 'r-', label='y(kx1)')
plt.plot(t, k_times_y1, 'b--', label='k*y(x1)')
plt.title(f"非线性系统齐次性验证 (k={k})")
plt.xlabel("时间 t")
plt.legend()
plt.grid(True)

# 线性系统验证
y1_l = system2(x1)
y2_l = system2(x2)
y_sum_l = system2(x1 + x2)
y1_plus_y2_l = y1_l + y2_l

y_scaled_l = system2(k*x1)
k_times_y1_l = k*y1_l

plt.subplot(2, 2, 3)
plt.plot(t, y_sum_l, 'r-', label='y(x1+x2)')
plt.plot(t, y1_plus_y2_l, 'b--', label='y(x1)+y(x2)')
plt.title("线性系统叠加性验证")
plt.xlabel("时间 t")
plt.legend()
plt.grid(True)

plt.subplot(2, 2, 4)
plt.plot(t, y_scaled_l, 'r-', label='y(kx1)')
plt.plot(t, k_times_y1_l, 'b--', label='k*y(x1)')
plt.title(f"线性系统齐次性验证 (k={k})")
plt.xlabel("时间 t")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

# 输出验证结果
print("非线性系统叠加性误差：", np.mean(np.abs(y_sum - y1_plus_y2)))
print("非线性系统齐次性误差：", np.mean(np.abs(y_scaled - k_times_y1)))
print("线性系统叠加性误差：", np.mean(np.abs(y_sum_l - y1_plus_y2_l)))
print("线性系统齐次性误差：", np.mean(np.abs(y_scaled_l - k_times_y1_l)))

图 11：线性系统与非线性系统的特性验证

二、时不变性

时不变系统：输入延迟 t0，输出也延迟 t0，即 T (x (t-t0)) = y (t-t0)。

三、因果性

因果系统：输出仅取决于当前及过去的输入，与未来输入无关。

四、稳定性

稳定系统：有界输入产生有界输出（BIBO 稳定）。

五、LTI 系统分析方法概述

LTI 系统（线性时不变系统）是信号与系统分析的核心，主要分析方法：

时域分析：卷积积分 / 卷积和
频域分析：傅里叶变换
复频域分析：拉普拉斯变换（连续系统）、Z 变换（离散系统）

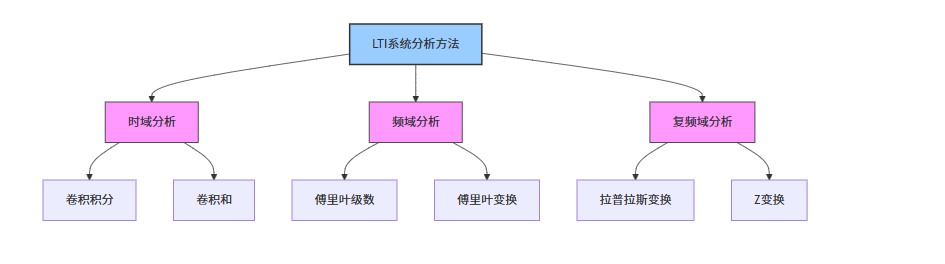
图 12：LTI 系统分析方法思维导图

通过本章学习，我们掌握了信号与系统的基本概念、信号分类、运算方法，以及系统的描述和特性分析，这些内容是后续深入学习信号处理的重要基础。

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-06-30，如有侵权请联系 cloudcommunity@tencent.com 删除

plot

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体同步曝光计划，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度