Design Theory for Relational Databases（关系型数据库）

Functional Dependencies

• X ->Y is an assertion about a relation R that whenever two tuples of R agree on all the attributes of X, then they must also agree on all attributes in set Y.

Say “X ->Y holds in R.” Convention: …, X, Y, Z represent sets of attributes; A, B, C,… represent single attributes. Convention: no set formers in sets of attributes, just ABC, rather than {A,B,C }.

Splitting Right Sides of FD’s

• X->A1A2…An holds for R exactly when each of X->A1 , X->A2 ,…, X->An hold for R.

Example: A->BC is equivalent to A->B and A->C.

• There is no splitting rule for left sides.

We’ll generally express FD’s with singleton right sides（通常将函数依赖标识为右侧单一属性形式）

Example: FD’s

Drinkers(name, addr, beersLiked, manf, favBeer)

• Reasonable FD’s to assert:

name -> addr favBeer

• Note this FD is the same as name -> addr and name -> favBeer.

beersLiked -> manf

Keys of Relations

• K is a superkey for relation R if K functionally determines all of R.（超键，能函数的决定关系中的所有属性）
• K is a key for R if K is a superkey, but no proper subset of K is a superkey（最小的超键）

Example: Superkey

• Drinkers(name, addr, beersLiked, manf, favBeer) {name, beersLiked} is a superkey because together these attributes determine all the other attributes.

name -> addr favBeer beersLiked -> manf

Example: Key（候选键）

• {name, beersLiked} is a key because neither {name} nor {beersLiked} is a superkey.

name doesn’t -> manf beersLiked doesn’t -> addr.

• There are no other keys, but lots of superkeys. Any superset of {name, beersLiked}（任何包含name、beersLiked都是超键）

Where Do Keys Come From?

• Just assert a key K. The only FD’s are K -> A for all attributes A.
• Assert FD’s and deduce the keys by systematic exploration（声明函数依赖，然后通过系统的分析推导出键值）

Inferring FD’s

• We are given FD’s X1 -> A1 , X2 -> A2 ,…, Xn -> An , and we want to know whether an FD Y ->B must hold in any relation that satisfies the given FD’s.

Example: If A -> B and B -> C hold, surely A -> C holds, even if we don’t say so.

• Important for design of good relation schemas（对于良好关系的设计至关重要）

Closure Test（闭包检测）

• An easier way to test is to compute the closure of Y, denoted Y +

Basis: Y + = Y（初始化闭包） Induction: Look for an FD’s left side X that is a subset of the current Y + If the FD is X -> A, add A to Y +

使用闭包检测还可以用来寻找候选键：

Finding All Implied FD’s（检查隐式的函数依赖）

• Motivation: “normalization（规范）” the process where we break a relation schema into two or more schemas.

Example: ABCD with FD’s AB ->C, C ->D, and D ->A. Decompose into ABC, AD. What FD’s hold in ABC ? Not only AB ->C, but also C ->A !

Basic Idea

• Start with given FD’s and find all FD’s that follow from the given FD’s.

Nontrivial = right side not contained in the left.

• Restrict to those FD’s that involve only attributes of the projected schema

Simple, Exponential Algorithm

• For each set of attributes X, compute X +
• Add X ->A for all A in X + - X
• However, drop XY ->A whenever we discover X ->A. （Because XY ->A follows from X ->A in any projection）
• Finally, use only FD’s involving projected attributes

A Few Tricks

• No need to compute the closure of the empty set or of the set of all attributes.
• If we find X = all attributes, so is the closure of any superset of X（如X是所有属性集，那么X任意超集的闭包也包含所有属性）

Example: Projecting FD’s

ABC with FD’s A ->B and B ->C.

Project onto AC.

• A +=ABC ; yields A ->B, A ->C.

We do not need to compute AB + or AC +

• B +=BC ; yields B ->C.
• C +=C ; yields nothing.
• BC +=BC ; yields nothing

Resulting FD’s: A ->B, A ->C, and B ->C. Projection onto AC : A ->C. Only FD that involves a subset of {A,C }.

Decomposition into BCNF

Given: relation R with FD’s F.

• Look among the given FD’s for a BCNF violation X ->Y.

If any FD following from F violates BCNF, then there will surely be an FD in F itself that violates BCNF.

• Compute X + .

Not all attributes, or else X is a superkey.

• Decompose R Using X -> Y
• Replace R by relations with schemas:

R1 = X +. R2 = R – (X + – X ).

• Project given FD’s F onto the two new relations.

Example: BCNF Decomposition

Drinkers(name, addr, beersLiked, manf, favBeer)

F = name->addr, name -> favBeer, beersLiked->manf

• Pick BCNF violation name->addr.
• Close the left side: {name} + = {name, addr, favBeer}.

Decomposed relations: Drinkers1(name, addr, favBeer) Drinkers2(name, beersLiked, manf)

• Thus, {name} is the only key and Drinkers1 is in BCNF.

For Drinkers2(name, beersLiked, manf), the only FD is beersLiked->manf,and

the only key is {name, beersLiked}.

• Violation of BCNF.
• beersLiked+ = {beersLiked, manf},

so we decompose Drinkers2 into: Drinkers3(beersLiked, manf) Drinkers4(name, beersLiked)

• The resulting decomposition of Drinkers :

Drinkers1(name, addr, favBeer) Drinkers3(beersLiked, manf) Drinkers4(name, beersLiked)

Third Normal Form -- Motivation

• There is one structure of FD’s that causes trouble when we decompose. AB ->C and C ->B.

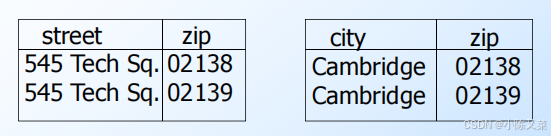
Example: A = street address, B = city, C = zip code. There are two keys, {A,B } and {A,C }. C ->B is a BCNF violation, so we must decompose into AC, BC.

We Cannot Enforce FD’s（无法强制实施函数依赖，函数依赖的丢失）

• The problem is that if we use AC and BC as our database schema, we cannot enforce the FD AB ->C by checking
• Example with A = street, B = city, and C = zip

3NF Let’s Us Avoid This Problem

• Normal Form (3NF) modifies the BCNF condition so we do not have to decompose in this problem situation.
• An attribute is prime if it is a member of any key.

X ->A violates 3NF if and only if X is not a superkey, and also A is not prime.（当且仅当X不是超键且A不是主属性）

What 3NF and BCNF Give You

There are two important properties of a decomposition:

1. Lossless Join : it should be possible to project the original relations onto the decomposed schema, and then reconstruct the original.
2. Dependency Preservation : it should be possible to check in the projected relations whether all the given FD’s are satisfied.

• We can get (1) with a BCNF decomposition.
• We can get both (1) and (2) with a 3NF decomposition.
• But we can’t always get (1) and (2) with a BCNF decomposition.

2NF

R is in 2NF if every nonprime attribute A in R is fully functionally dependent on every key of R

（任何一个非主属性必定完全函数依赖与候选键）

Full Functional Dependency

• Y is 'fully functionally dependent' on X if it is dependent on all of X, not on any part of X.

X ->Y not on any part X’ of X, X ’ ->Y

Full Functional Dependency A FD X→Y is a full functional dependency

if the removal of any attribute from X means the dependency does not hold any more.