数据存储（浮点型）

浮点数的存储与整型的存储是有很大区别的，而不是简单的把浮点数转化为二进制补码进行存储。

​

1.科学计数法

根据国际标准IEEE 754 任意浮点数，都可以写为

V = (-1)^S * M * 2^ E

(-1)^S为符号位，S=0时V为正，S=1时V为负。

M为有效数字，1<m<2

2^ E为指数位。

注：（^表示幂运算，如2^E表示2的E次方）

V = (-1)^s * M * 2^ E，其实是二进制的科学计数法。

V = (-1)^s * M * 8^ E，是八进制的科学计数法。

V = (-1)^s * M * 10^ E，是十进制的科学计数法。

编译器会将所需存储的浮点型数字转化为二进制，然后对它科学计数后的S,M,E进行存储

举个例子

十进制的5.5转化为二进制为101.1即1.011*2^2,那么S=0,M=1.01,E=2。

IEEE 754 规定：

float类型(占4个字节即32个比特位)最高位的1个比特位来存储S，后8个比特位来存储E，最后的23个比位用来存储M，如图：

6c63494068574947add232c5d5374c82.png

double类型(占8个字节即64个比特位)最高位的1个比特位来存储S，后11个比特位来存储E最后的52个比位用来存储M，如图：

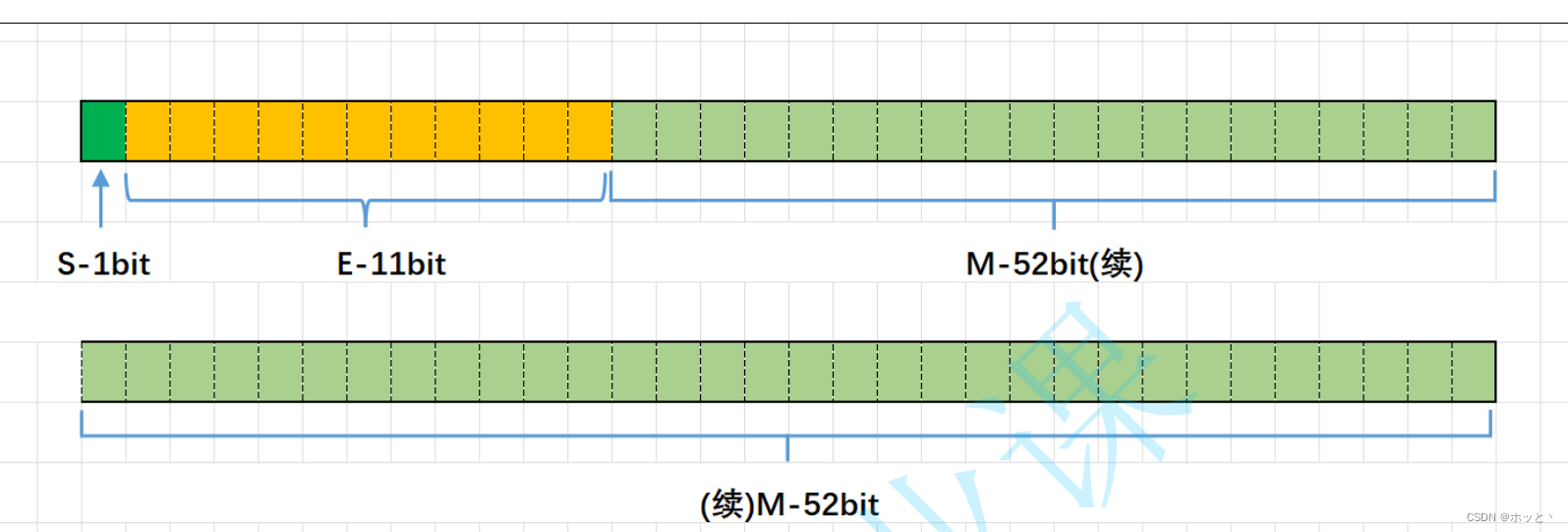
fd7f13ad44ce414795356447562a4084.png

2.S的储存

S的储存比较简单如果数字是正数就储存0，反之则储存1。

3.E的存储(以float类型为例子)

E是当作unsigned int来存储的，最高位并不是符号位，所以存储范围是0~255，指数位E是没必要达到一两百，而且E可能存在负数，所以IEEE 75规定对E加上127后转化为二进制再进行存储。

例如：十进制的5.5，二进制为101.1即1.011*2^2，E=2，储存的是2+127即：100000001

4.M的存储

M存储时只对小数点后的数据存储，而舍去前面的1，从而可以达到提高精度，而在取的时候自动补上1，例如

1.1011*2^4（假设为float型）。M位置只需要存1011，不够23位就往后面补零，即：

10110000000000000000000

5.精度问题

有很多浮点数是不能精确保存的，也就是有精度损失，这是因为有很多浮点数是无法写成它准确的科学计数法的，例如3.14，1.97等等。

5.浮点数取的过程

指数E从内存中取出分成三种情况：

5.1.E不全为0或不全为1

这时，浮点数就采⽤下⾯的规则表⽰，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第⼀位的1。

5.2.E全为0

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，有效数字M不再加上第⼀位的1，⽽是还原为0.xxxxxx的⼩数。这样做是为了表⽰±0，以及接近于0的很⼩的数字。

5.3.E全为1

这时，如果有效数字M全为0，表⽰±⽆穷⼤（正负取决于符号位s）；

点击下面链接了解整型的存储：

https://blog.csdn.net/2302_80105876/article/details/134593555