绘制蟒蛇三维等深面图
绘制蟒蛇三维等深面图
提问于 2020-04-29 10:41:09
我试图在python中为给定的omega值使用plot或matplotlib绘制以下函数:
omega = (1/(12*np.pi*r**3)*((3*np.cos(THETA)**2-1)+1.5*np.sin(THETA)**2*np.cos(2*PHI)))为此,我指定omega的值,计算r,然后从极坐标转换为笛卡尔坐标。
import numpy as np
import plotly.graph_objects as go
omega = 10
theta, phi = np.linspace(0,2*np.pi, 400), np.linspace(0,np.pi, 400)
THETA,PHI = np.meshgrid(theta,phi)
#Calculate R for a given value of omega
R1 = (1/(12*np.pi*omega)*((3*np.cos(THETA)**2-1)+1.5**np.sin(THETA)**2*np.cos(2*PHI)))
R = np.sign(R1) * (np.abs(R1))**(1/3)
#Convert to cartesians
X = R * np.sin(PHI) * np.cos(THETA)
Y = R * np.sin(PHI) * np.sin(THETA)
Z = R * np.cos(PHI)
#Plot isosurface plot
fig = go.Figure(data=[go.Surface(z=Z, x=X, y=Y)])
fig.show()然而,通过这样做,我失去了关于正叶和负叶的信息,也就是这里的两者都是绘制出来的。
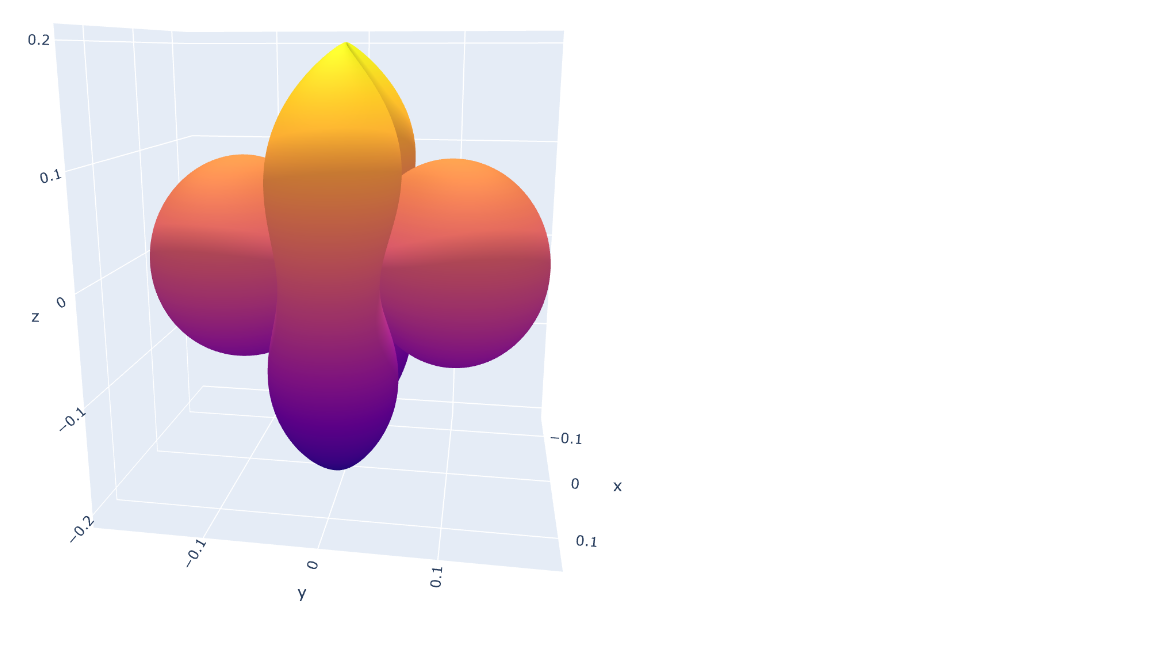
我可以通过将omega的负值设置为NaN来解决这个问题。这关闭了负片,但结果是为图形绘制手工艺品。
import numpy as np
import plotly.graph_objects as go
omega = 10
theta, phi = np.linspace(0,2*np.pi, 400), np.linspace(0,np.pi, 400)
THETA,PHI = np.meshgrid(theta,phi)
#Calculate R for a given value of omega
R1 = (1/(12*np.pi*omega)*((3*np.cos(THETA)**2-1)+1.5**np.sin(THETA)**2*np.cos(2*PHI)))
R = np.sign(R1) * (np.abs(R1))**(1/3)
#Remove negative lobes
R[R1 < 0.] = np.NaN
#Convert to cartesians
X = R * np.sin(PHI) * np.cos(THETA)
Y = R * np.sin(PHI) * np.sin(THETA)
Z = R * np.cos(PHI)
#Plot isosurface plot
fig = go.Figure(data=[go.Surface(z=Z, x=X, y=Y)])
fig.show()
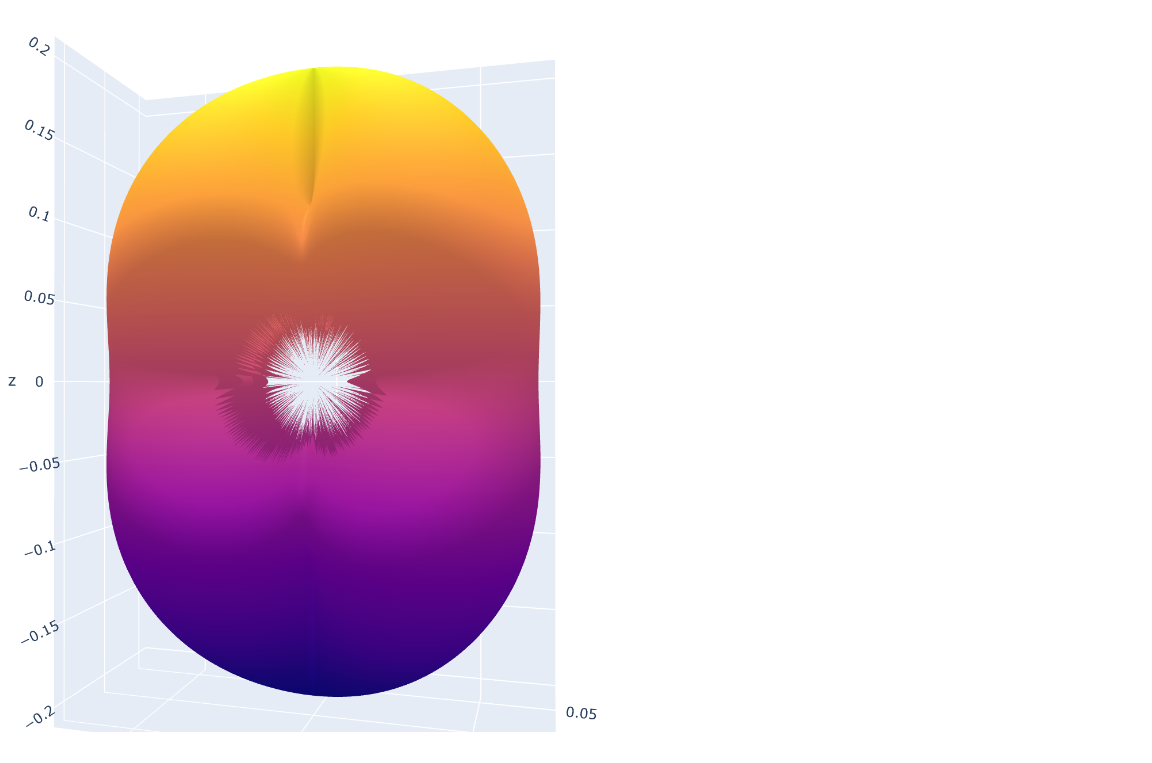
我不知道如何克服这个问题--如果我增加THETA和PHI的点数,则图形呈现得非常慢,而且仍然不可能增加足够多的点数来完全删除人工制品。理想情况下,我会将r、theta和phi值传递给绘图函数,并按给定的omega值绘制等深面,但这仅在cartesians中是可能的。将整个函数转换为cartesians将导致f(x,y,z,r),这也是我无法绘制的。
回答 1
Stack Overflow用户
发布于 2021-10-15 11:27:31
你会发现这里是一种内置的方法,可以用pyvista绘制等深线。
或者您可以使用行军立方体的实现 (来自R包misc3d的原始代码):
from math import cos, sin
def f(ρ, θ, ϕ):
return (1/(12*np.pi*ρ**3)*((3*cos(θ)**2-1)+1.5*sin(θ)**2*cos(2*ϕ)))
ρmax = 0.3
θmax = 4*np.pi
ϕmax = 2*np.pi
nρ = 200
nθ = 200
nϕ = 200
mesh = marchingCubes(
f, 10, 0.001, ρmax, 0, θmax, 0, ϕmax, nρ, nθ, nϕ
)
print(mesh)
def sph2cart(sph):
ρ = sph[0]
θ = sph[1]
ϕ = sph[2]
return [
ρ * cos(θ) * sin(ϕ),
ρ * sin(θ) * sin(ϕ),
ρ * cos(ϕ)
]
mesh.points = np.apply_along_axis(sph2cart, 1, mesh.points)
mesh.plot(smooth_shading=True, specular=5, color="purple")我发现θ必须是4pi,phi必须是2pi,否则曲面不是封闭的。结果如下:

观察中心的洞。它对应于rho的最小值(不能将其设置为0,否则就会被除以零)。
现在,如果您想在中巧妙地获取这个曲面,您可以从mesh对象中提取顶点和面(三角形),并巧妙地使用Mesh3d:
vertices = mesh.points
triangles = mesh.faces.reshape(-1, 4)
import plotly.graph_objects as go
import plotly.io as pio
fig = go.Figure(data=[
go.Mesh3d(
x=vertices[:,0],
y=vertices[:,1],
z=vertices[:,2],
colorbar_title='z',
colorscale=[[0, 'gold'],
[0.5, 'mediumturquoise'],
[1, 'magenta']],
# i, j and k give the vertices of triangles
i=triangles[:,1],
j=triangles[:,2],
k=triangles[:,3],
name='y',
showscale=True
)
])
#fig.show()
pio.write_html(fig, file='SO.html', auto_open=True)

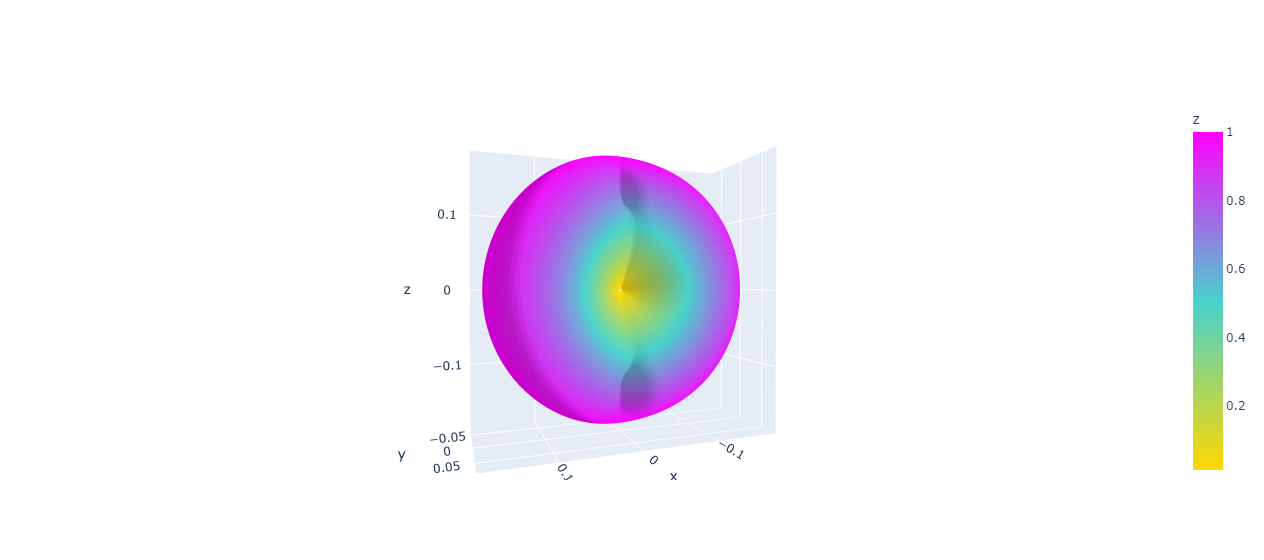
要获得颜色:
distances = np.linalg.norm(vertices, axis=1)
distances = distances / (distances.max())
fig = go.Figure(data=[
go.Mesh3d(
x=vertices[:,0],
y=vertices[:,1],
z=vertices[:,2],
colorbar_title='z',
colorscale=[[0, 'gold'],
[0.5, 'mediumturquoise'],
[1, 'magenta']],
# Intensity of each vertex, which will be interpolated and color-coded
intensity=distances,
# i, j and k give the vertices of triangles
i=triangles[:,1],
j=triangles[:,2],
k=triangles[:,3],
name='y',
showscale=True
)
])
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/61509272
复制相关文章
相似问题
社区富文本编辑器全新改版!诚邀体验~
全新交互,全新视觉,新增快捷键、悬浮工具栏、高亮块等功能并同时优化现有功能,全面提升创作效率和体验
