【数据结构】链式结构二叉树详解
一、实现方法
1.1 链式存储的底层原理
与堆不同,在链式结构中,二叉树是由一个个节点组成的,而每个节点都由三部分构成。 分别是:
- 左指针:指向左子节点(左孩子)
- 右指针:指向右子节点
- 数据域:存储节点的值
链式结构二叉树节点的子节点不会超过两个,我们要能够找到这两个子节点,自然需要两个指针,左指针存储左孩子的地址,右指针存储右孩子的地址。当然,节点本身也是要存点东西的,数据。
代码实现:
typedef int BTDataType;//重命名:方便以后存储其他类型时,一键修改,且不会影响到以int 类型定义的变量
//定义链式二叉树节点结构
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;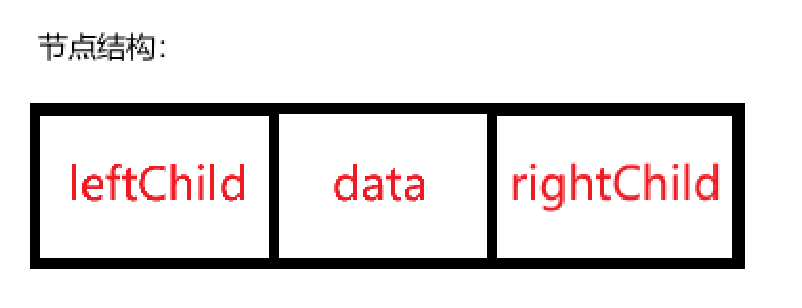
在这里插入图片描述
1.2 创建链式二叉树
创建链式二叉树自然离不开创建节点来准备用来拼装的积木,之后再一点点按照想法组装就好了 1.创建节点 2.组装
1.2.1 创建节点
代码实现:
//根据x创造节点
BTNode* BTbuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(1);
}
newnode->left = newnode->right = NULL;//置空
newnode->data = x;
return newnode;
}BTNode* Node1 = BTbuyNode(1);
BTNode* Node2 = BTbuyNode(2);
BTNode* Node3 = BTbuyNode(3);
BTNode* Node4 = BTbuyNode(4);
BTNode* Node5 = BTbuyNode(5);
BTNode* Node6 = BTbuyNode(6);1.2.2 组装(接下来都以我们创建的二叉树为例)
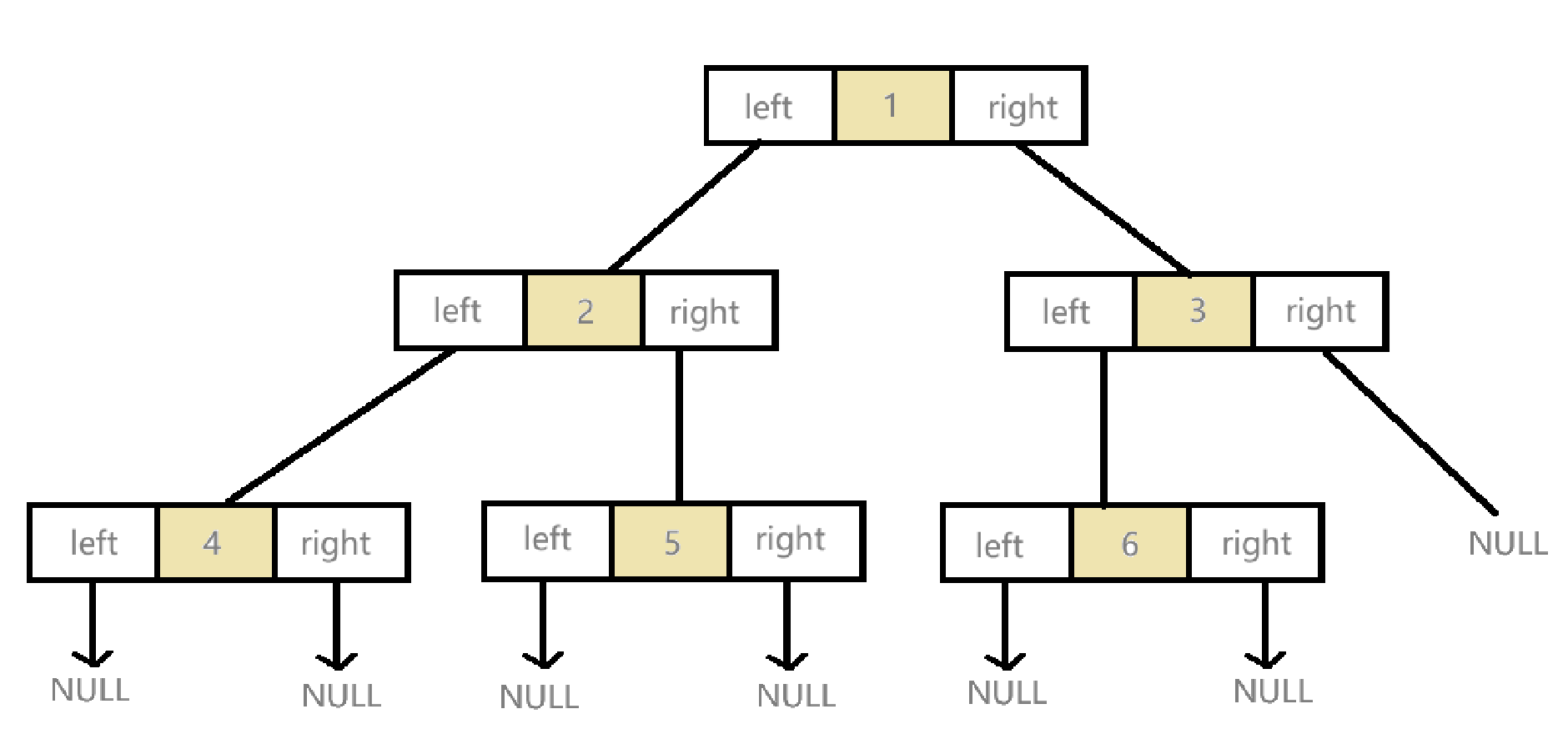
我们想创造一个结构如下图的二叉树(可以不必是完全二叉树),需要进行组装,即链接。
在这里插入图片描述
- 没有左孩子或右孩子的时候对应指针指向空。
代码实现:
//组装
Node1->left = &Node2;
Node1->right = &Node3;
Node2->left = &Node4;
Node2->right = &Node5;
Node3->left = &Node6;1.2.3 完整代码
//根据x创造节点
BTNode* BTbuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(1);
}
newnode->left = newnode->right = NULL;
newnode->data = x;
return newnode;
}
//创建二叉树
BTNode* CreatebinaryTree()
{
BTNode* Node1 = BTbuyNode(1);
BTNode* Node2 = BTbuyNode(2);
BTNode* Node3 = BTbuyNode(3);
BTNode* Node4 = BTbuyNode(4);
BTNode* Node5 = BTbuyNode(5);
BTNode* Node6 = BTbuyNode(6);
//组装
Node1->left = Node2;
Node1->right = Node3;
Node2->left = Node4;
Node2->right = Node5;
Node3->left = Node6;
return Node1;
}2.2 前中后序遍历(递归)
介绍: 前序遍历:访问根节点的操作在遍历它的左右子树之前。
- 顺序:根节点,左子树,右子树
中序遍历:访问根节点的操作在遍历它的左右子树之间。
- 顺序:左子树,根节点,右子树
后序遍历:访问根节点的操作在遍历它的左右子树之后。
- 顺序:左子树,右子树,根节点
2.2.1 前序遍历(根左右)
遍历思路图:
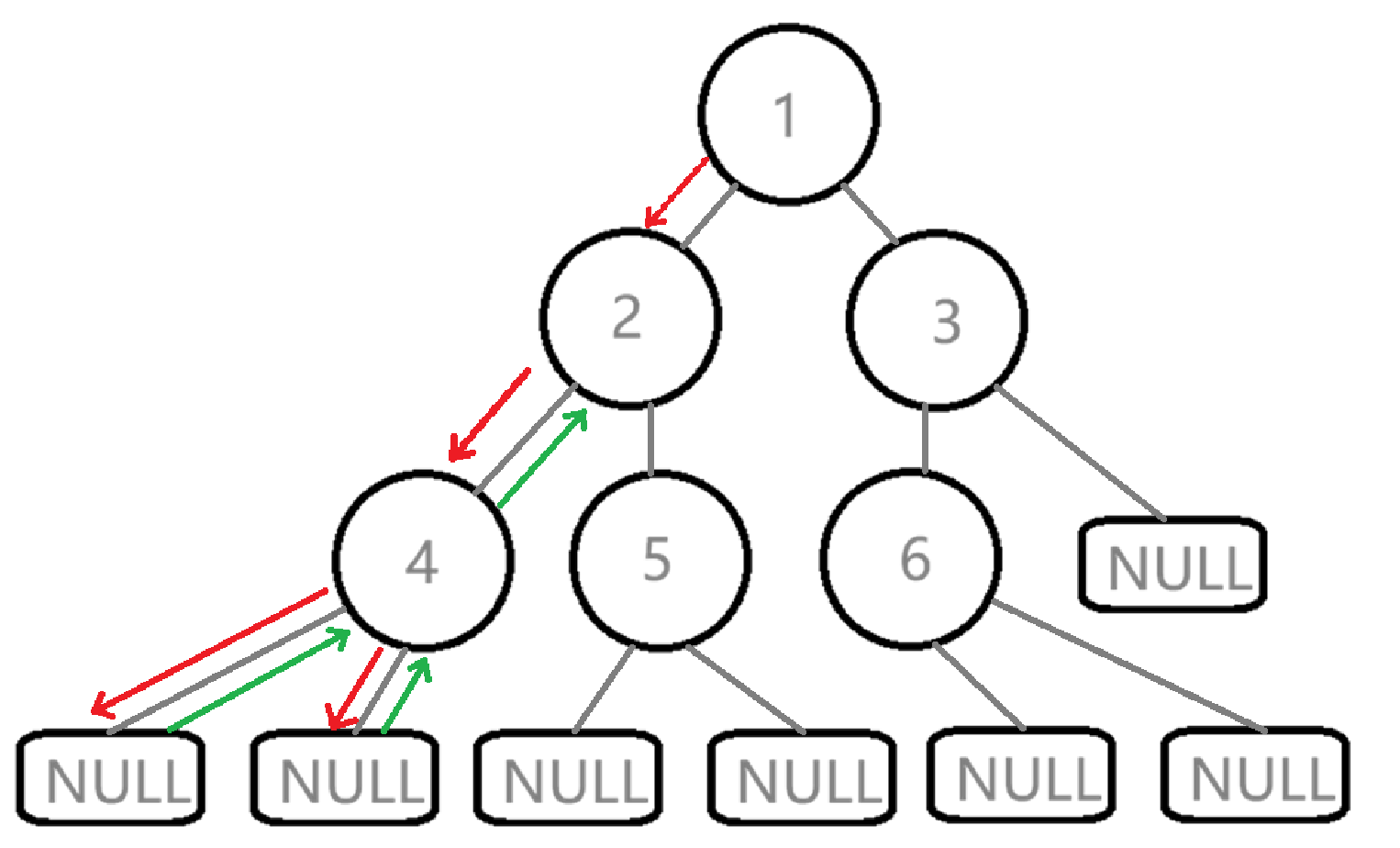
在这里插入图片描述
路程如图: 1.前序遍历先访问值为1的根,打印1。 2.再遍历它值为2的左子树,值为2的左子树是一棵二叉树,打印2。 3.继续遍历值为2的左子树的值为4的左子树,打印4。 4.遍历值为4 的节点,先访问左子树,遇到NULL返回,再访问右子树,遇到NULL返回。 5.值为4的节点的左右子树遍历完成,返回值为2的父节点。值为2的节点的左子树遍历完成。
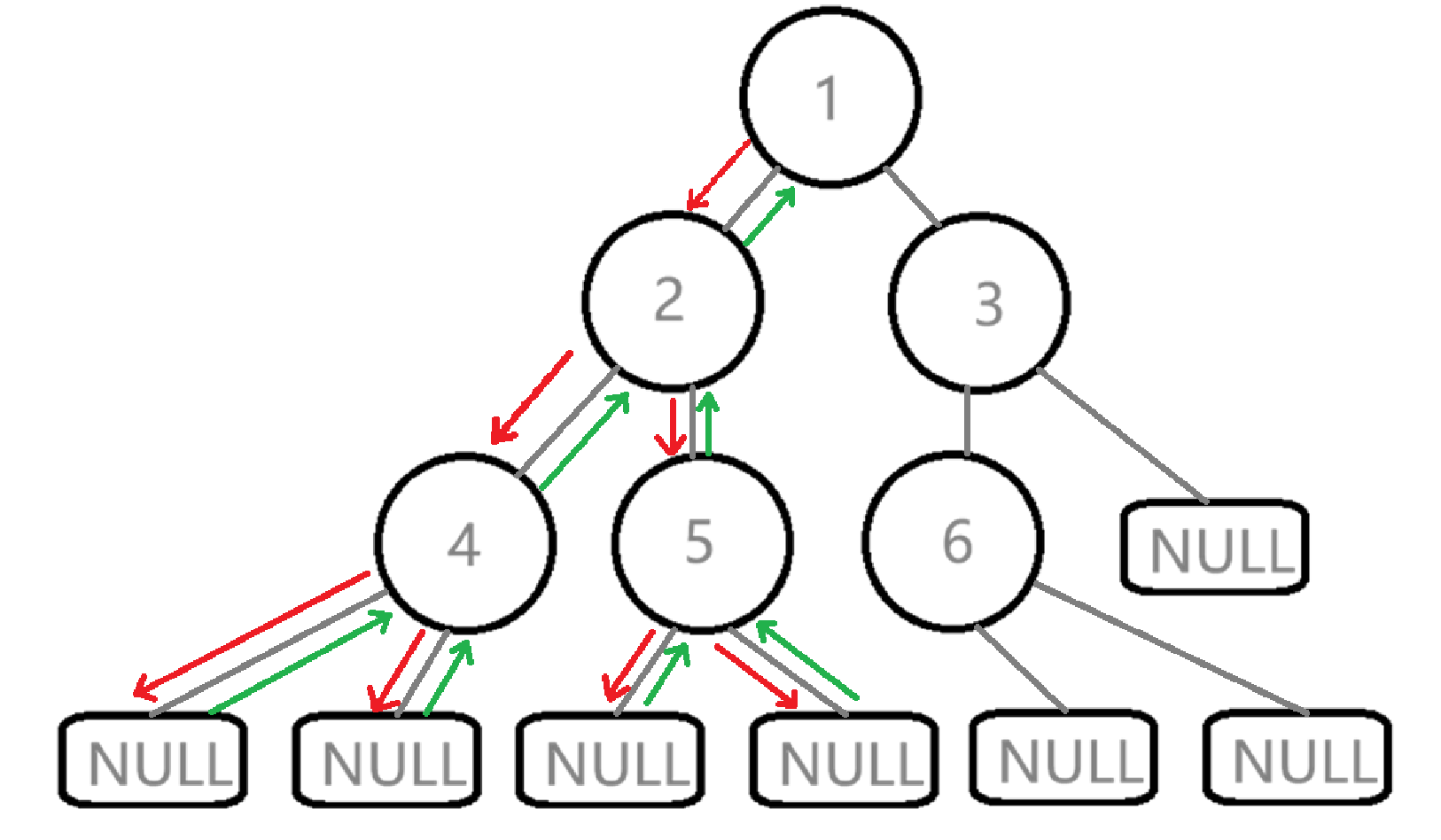
在这里插入图片描述
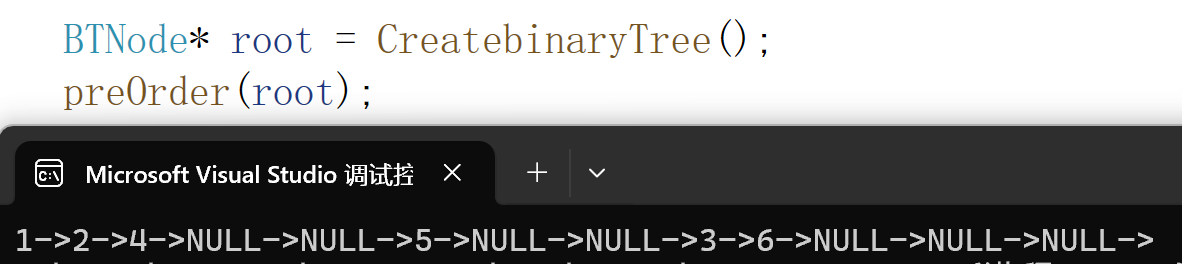
6.遍历值为2的节点的右子树,打印5。 7.遍历值为5的节点,先访问左子树,遇到NULL返回,再访问右子树,遇到NULL返回。 8.值为5的节点的左右子树遍历完成,返回值为2的父节点。 9.值为2的节点的左右子树遍历完成,返回值为1的根节点。 10.根节点的左子树遍历完成,接下来遍历右子树,与左子树差不多。 前序遍历顺序: 1->2->4->NULL->NULL->5->NULL->NULL->3->6->NULL->NULL->NULL
一些要点:
- 前序遍历就跟挖土豆一样,挖到一个拿一个,只不过我们总是先挖左边的土豆,直到左边的土豆都挖完,再挖右边的(同层节点:左子树优先于右子树)。
- 直到把所有的土豆都挖完,遍历完成。
思路:二叉树由三部分组成,根节点,根的左子树,根的右子树。根的左子树也是一颗二叉树,我们同样可以根据结构把它们分为小根节点(不是根节点,代称),小根节点的左子树,小根节点的右子树(右子树同样)。遍历规则就是:先遍历根节点,再把左子树遍历完成之后再遍历完右子树。小根节点二叉树也是这样,以此类推。->递归
代码实现:
//前序遍历-根左右
void preOrder(BTNode* root)
{
//遇到NULL就返回
if (root == NULL)
{
printf("NULL->");
return;
}
printf("%d->", root->data);//打印节点的值
preOrder(root->left);//遍历左子树
preOrder(root->right);//遍历右子树
}可以结合思路图一起理解。
执行结果:
在这里插入图片描述
2.2.2 中序遍历(左根右)
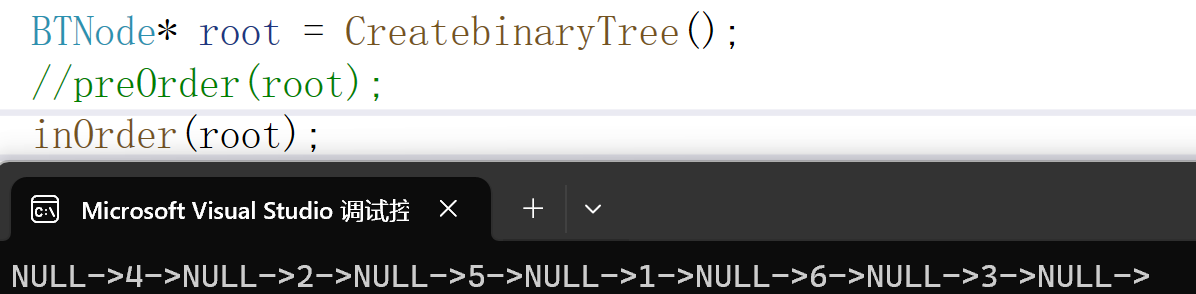
理解了前序遍历之后,其他的便很好理解,这里就不作图了。 中序遍历顺序: NULL->4->NULL->2->NULL->5->NULL->1->NULL->6->NULL->3->NULL
思路: 二叉树由三部分组成,根节点,根的左子树,根的右子树。根的左子树也是一颗二叉树,我们同样可以根据结构把它们分为小根节点(不是根节点,代称),小根节点的左子树,小根节点的右子树(右子树同样)。遍历规则就是:先遍历完左子树,再访问根节点,之后再遍历完右子树。小根节点二叉树也是这样,以此类推。->递归
代码实现:
//中序遍历-左根右
void inOrder(BTNode* root)
{
//遇到NULL返回
if (root == NULL)
{
printf("NULL->");
return;
}
inOrder(root->left);//遍历左子树
printf("%d->", root->data);//打印
inOrder(root->right);//遍历右子树
}执行结果:
在这里插入图片描述
2.2.3 后序遍历(左右根)
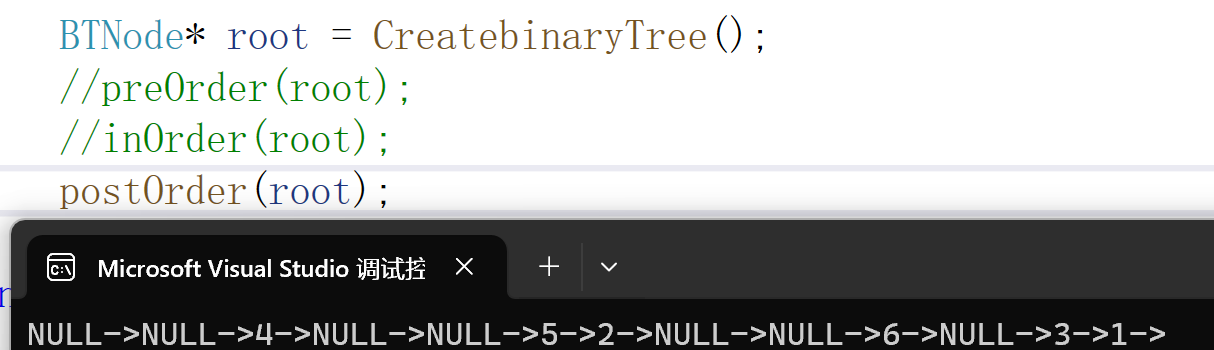
后序遍历顺序: NULL->NULL->4->NULL->NULL->5->2->NULL->NULL->6->NULL->3->1 代码实现:
思路: 二叉树由三部分组成,根节点,根的左子树,根的右子树。根的左子树也是一颗二叉树,我们同样可以根据结构把它们分为小根节点(不是根节点,代称),小根节点的左子树,小根节点的右子树(右子树同样)。遍历规则就是:先遍历完左子树,再遍历完右子树,最后访问根节点。小根节点二叉树也是这样,以此类推。->递归
代码实现:
//后续遍历-左右根
void postOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL->");
return;
}
postOrder(root->left);
postOrder(root->right);
printf("%d->", root->data);
}执行结果:
在这里插入图片描述
2.3 求二叉树节点个数
思路: 我们可以把二叉树分为三个部分:根节点,根结点的左子树与根节点的右子树。 那么是否有: 为空:返回0 不为空: 结点个数 = 根节点(1)+ 左子树节点个数 + 右子树节点个数 ->递归
- 碰到NULL就返回0
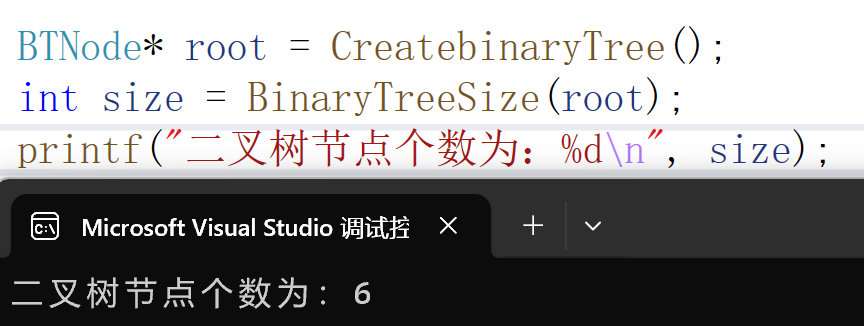
代码实现:
int BinaryTreeSize(BTNode* root)
{
//自身为空返回0
if (root == NULL)
{
return 0;
}
//不为空,返回根节点(1)+ 左子树节点个数 +左子树节点个数
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}- 就不作递归的完整图了,只要能get到就好
执行结果:
在这里插入图片描述
2.4 求二叉树叶子节点个数
思路: 二叉树可分为:根节点,根节点的左子树,根节点的右子树 是否有: 二叉树叶子节点个数 = 左子树叶子节点个数 + 右子树节点个数 什么是叶子节点?->本身不为空,但左右子树皆为空的节点
代码实现:
//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
//自身不能为空
if (root == NULL)
{
return 0;
}
//左右子树要皆为空
if (root->left == NULL && root->right == NULL)
{
return 1;
}
//返回左子树叶子节点个数 + 右子树节点个数
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}执行结果:
在这里插入图片描述
2.5 求二叉树第k层节点个数
思路: 二叉树可分为:根节点,根节点的左子树,根节点的右子树 是否有: 二叉树第k层节点个数 = 左子树第k层节点个数 + 右子树第k层节点个数 求第k层节点个数,倘若我们每次递归之后 k-1 的话,当k = 1的时候代表我们所求层 若我们求第三层节点个数:
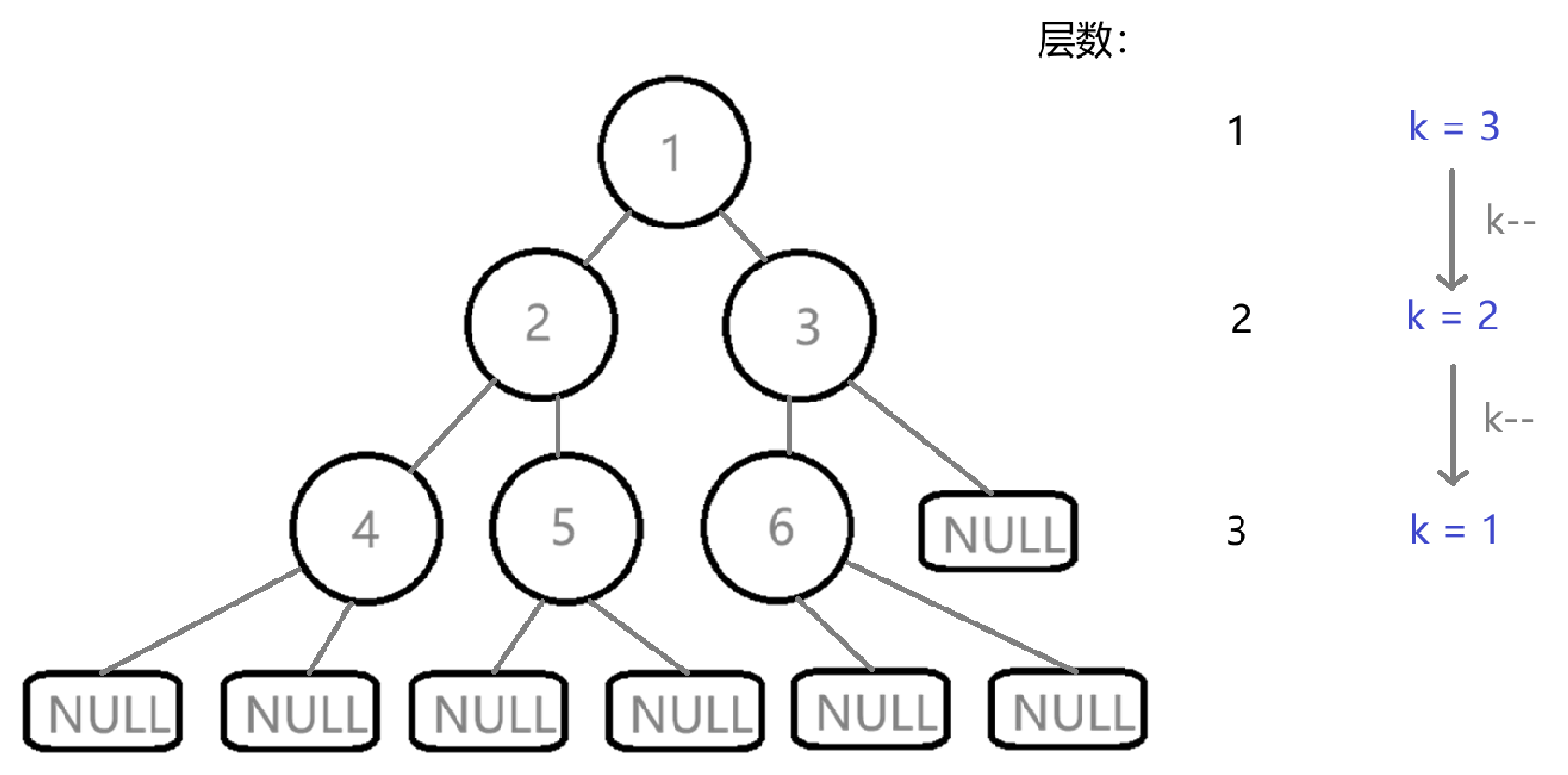
在这里插入图片描述
代码实现:
//二叉树第k层节点个数
int BinaryTreeLevelSize(BTNode* root, int k)
{
assert(k > 0)
if (root == NULL)
{
return 0;
}
//k等于1且不为空的时候返回1
if (k == 1)
{
return 1;
}
//返回左子树第k层节点个数 + 右子树第k层节点个数
return BinaryTreeLevelSize(root->left, k - 1) + BinaryTreeLevelSize(root->right, k - 1);
}2.6 二叉树的深度(高度)
思路: 二叉树可分为:根节点,根节点的左子树,根节点的右子树。 是否有: 为空:返回0 不会空: 二叉树的深度(高度) = 根节点(1) + max(左子树的深度,右子树的深度) 如何记录深度?->递归一次就是深入1层。挺像挖土,递归就像一把铲子,递归一次就铲一次,会铲的越来越深。铲了多少次就代表有多深。
代码实现:
//二叉树的深度(高度)
int BinaryTreeDepth(BTNode* root)
{
//为空:返回0
if (root == 0)
{
return 0;
}
//各自递归多少次leftDep和rightDep就是多少
int leftDep = BinaryTreeDepth(root->left);
int rightDep = BinaryTreeDepth(root->right);
//不为空,返回根节点(1) + max(左子树的深度,右子树的深度)
return 1 + (leftDep > rightDep ? leftDep : rightDep);
}执行结果:
在这里插入图片描述
图解:
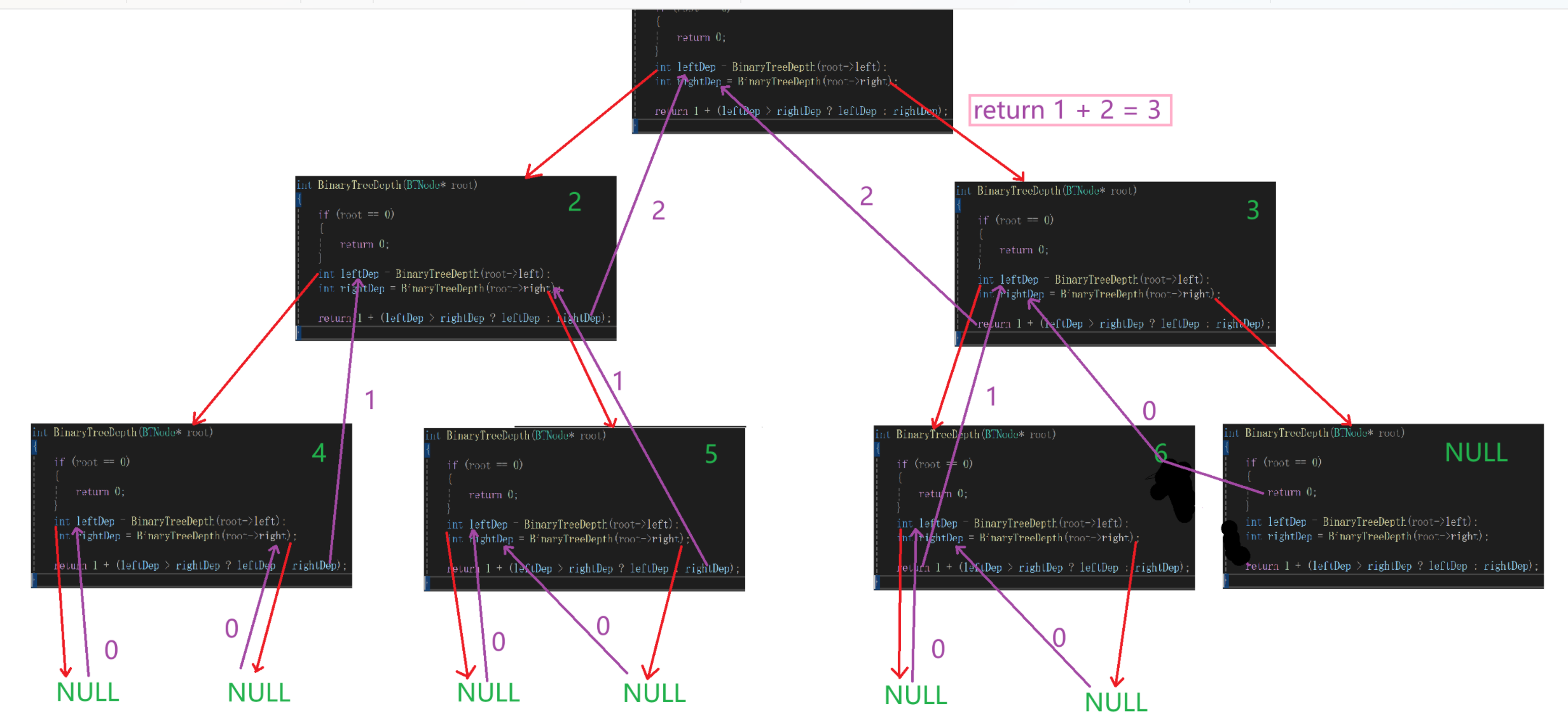
在这里插入图片描述
2.7 二叉树查找(可修改)值为x的点
思路: 二叉树可分为:根节点,根节点的左子树,根节点的右子树。 是否有: 先查根节点,再查左右子树
- 没找到则返回NULL
代码实现:
//查找二叉树中值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
//为空,返回NULL
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
//找左子树
BTNode* leftfind = BinaryTreeFind(root->left, x);
//若leftfind不为空
if (leftfind)
{
return leftfind;
}
//找右子树
BTNode* rightfind = BinaryTreeFind(root->right, x);
//若rightfind不会空
if (rightfind)
{
return rightfind;
}
//没找到,返回NULL
return NULL;
}执行结果:
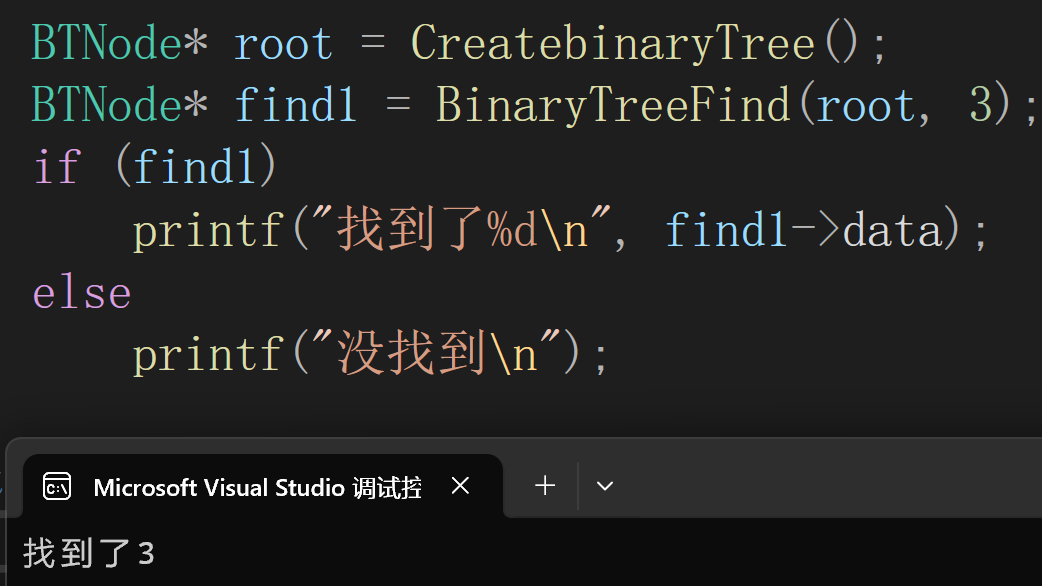
在这里插入图片描述
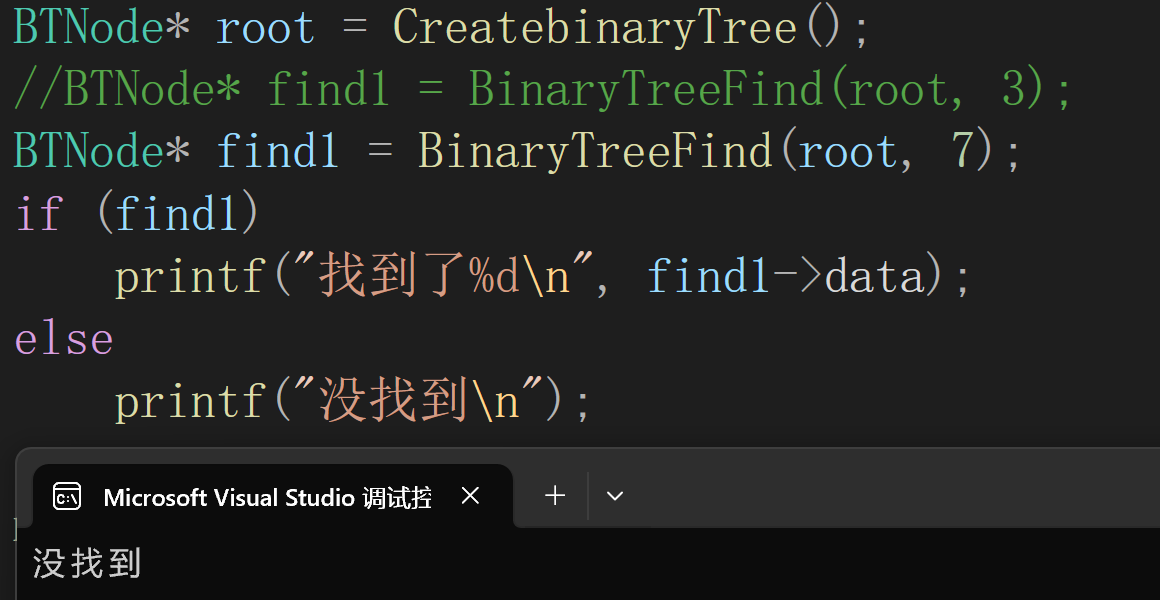
在这里插入图片描述
2.8 层序遍历
思路:我们的二叉树只能访问目前节点它的左子树和右子树,想要一层层遍历,就需要我们访问它的左孩子之后立刻访问它的右孩子,但是这样我们就不能往回去遍历左子树了,我们需要将节点顺序进行存储,再顺序拿出。符合先进先出规则,我们借助队列来实现。 1.借助队列保存根节点。 2.每次取出一个节点访问它的子节点,并打印节点的值。 3.非空子节点入队列。 4.迭代,重复步骤2,3直到队列为空。
流程图:
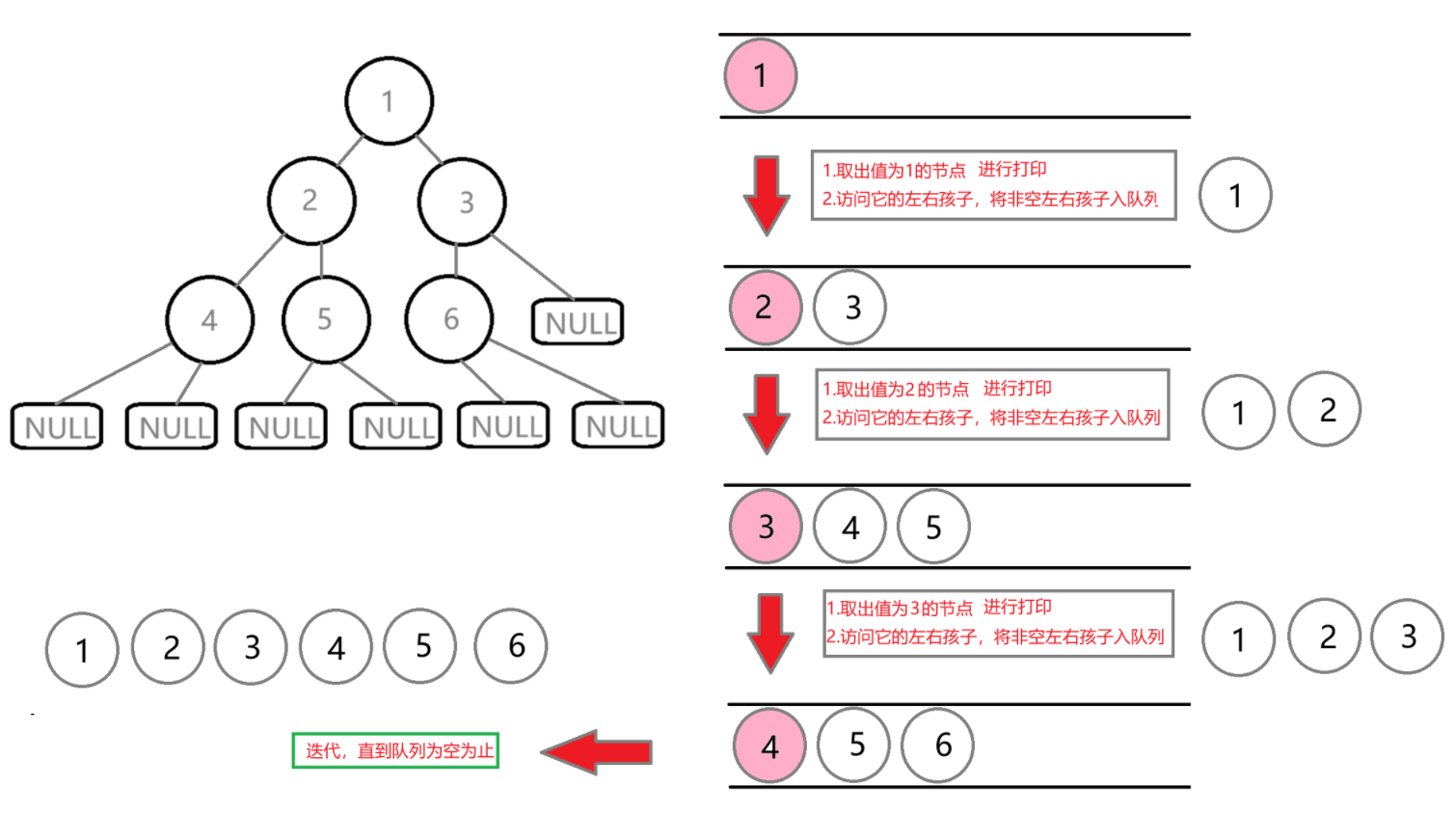
在这里插入图片描述
我们先要实现队列,可以进行拷贝。 1.修改Queue.h头文件中要保存的数据类型
//int 修改为 struct BinaryTreeNode,不能写成重命名后的类型名称,要告诉系统这是什么类型
typedef int QDataType;2.在tree.c包含队列的头文件
在这里插入图片描述
代码实现:
//层序遍历
void levelOrder(BTNode* root)
{
//传入空指针时直接返回
if (root == NULL)
return;
//创建队列
Queue q;
QueueInit(&q);
//将根节点存入队列
QueuePush(&q, root);
//迭代直到队列为空
while (!QueueEmpty(&q))
{
//取队头,出队头
BTNode* top = QueueFront(&q);
QueuePop(&q);
printf("%d ", top->data);
//将非空子节点存入队列
if (top->left)
QueuePush(&q, top->left);
if (top->right)
QueuePush(&q, top->right);
}
//销毁队列
QueueDesTory(&q);
}执行结果:
在这里插入图片描述
2.9 判断是否为完全二叉树
思路: 首先我们要知道什么是完全二叉树 — 1.最后一层节点个数不一定达到最大。2.从左到右依次排列 若有k个元素,完全二叉树的 k 个元素一定是像数组一样连续排列的,中间不可能为空,而非二叉树则没有这个要求。我们需要存储值来判断是否为空->借助队列。跟层序排列有点相像。 我们再画图分析一下: 完全二叉树:
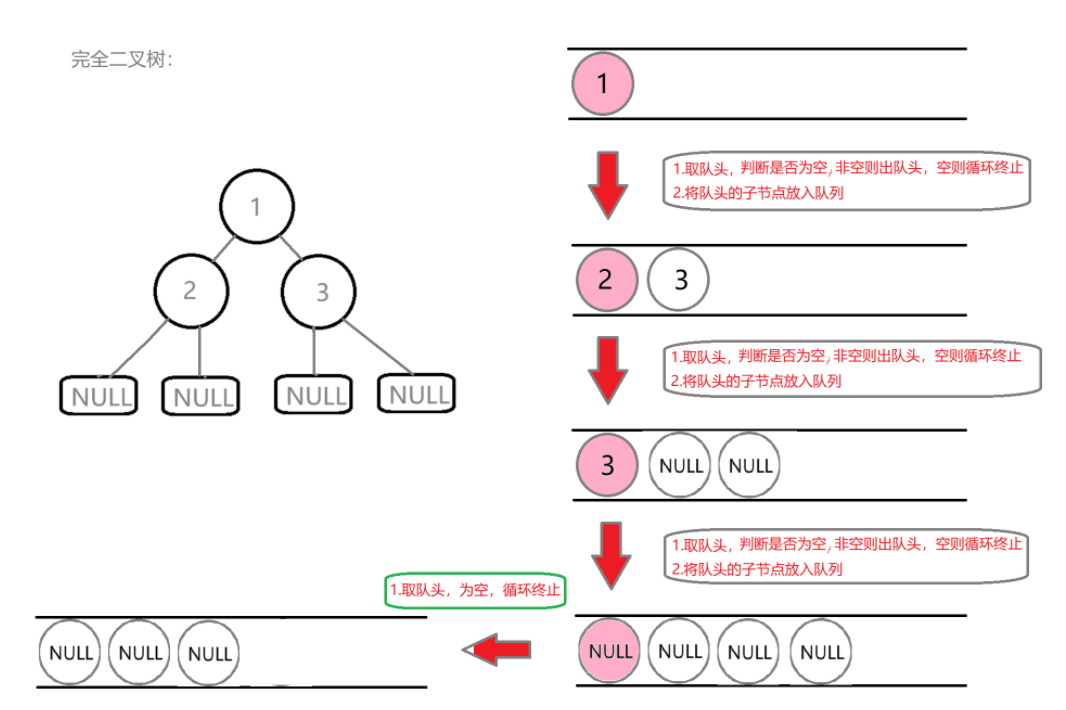
在这里插入图片描述
非完全二叉树:
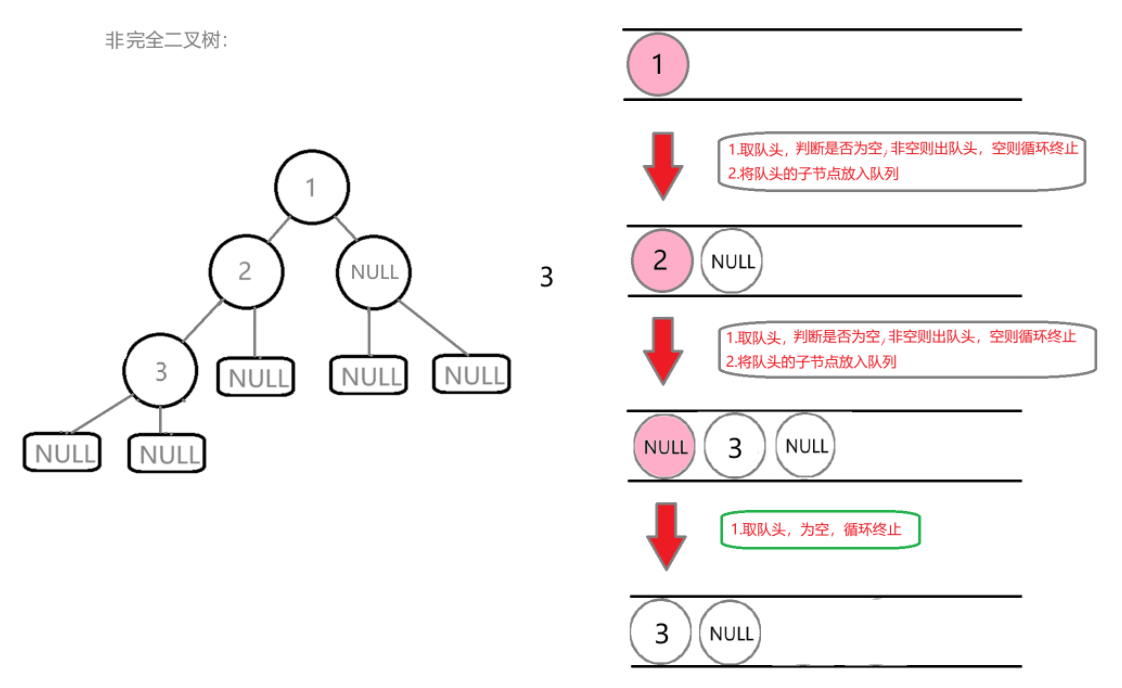
在这里插入图片描述
二者对比:
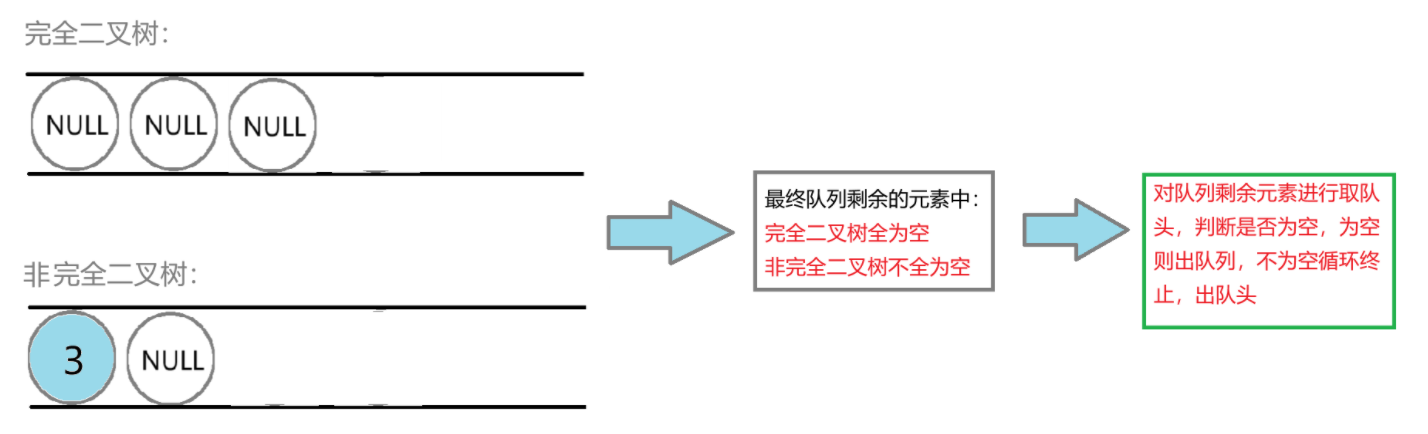
在这里插入图片描述
如果队列剩余元素皆为NULL->完全二叉树 不全为NULL->非完全二叉树 1.进行第一个循环,与层序遍历过程差不多,但是子节点的值是否为NULL都要入队列。而出队列则是碰到NULL停止。 2.第二个循环,遍历队列剩余元素,对队列取队头,判断是否为空,为空则出队列,不为空循环终止,出队头。
代码实现:
//判断是否为完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
//判断是否为空,为空直接返回
if (root == NULL)
return;
//创建队列
Queue q;
QueueInit(&q);
QueuePush(&q, root);
BTNode* top = QueueFront(&q);
//进行第一个循环
while (!QueueEmpty(&q))
{
top = QueueFront(&q);
QueuePop(&q);
if (top == NULL)
{
break;
}
QueuePush(&q, top->left);
QueuePush(&q, top->right);
}
//进行第二个循环
while (!QueueEmpty(&q))
{
top = QueueFront(&q);
QueuePop(&q);
if (top != NULL)
{
return false;
}
}
//销毁队列
QueueDesTory(&q);
return true;
}执行结果:
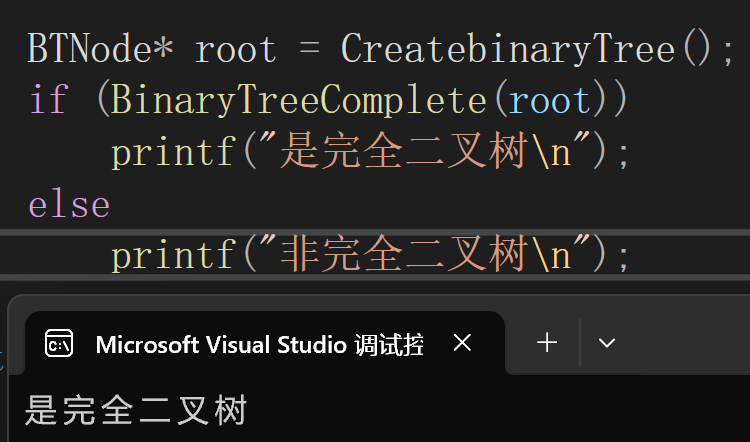
在这里插入图片描述
2.10 销毁
思路: 要释放所有节点的内存,用后序遍历,不会因为销毁节点而找不到位置。
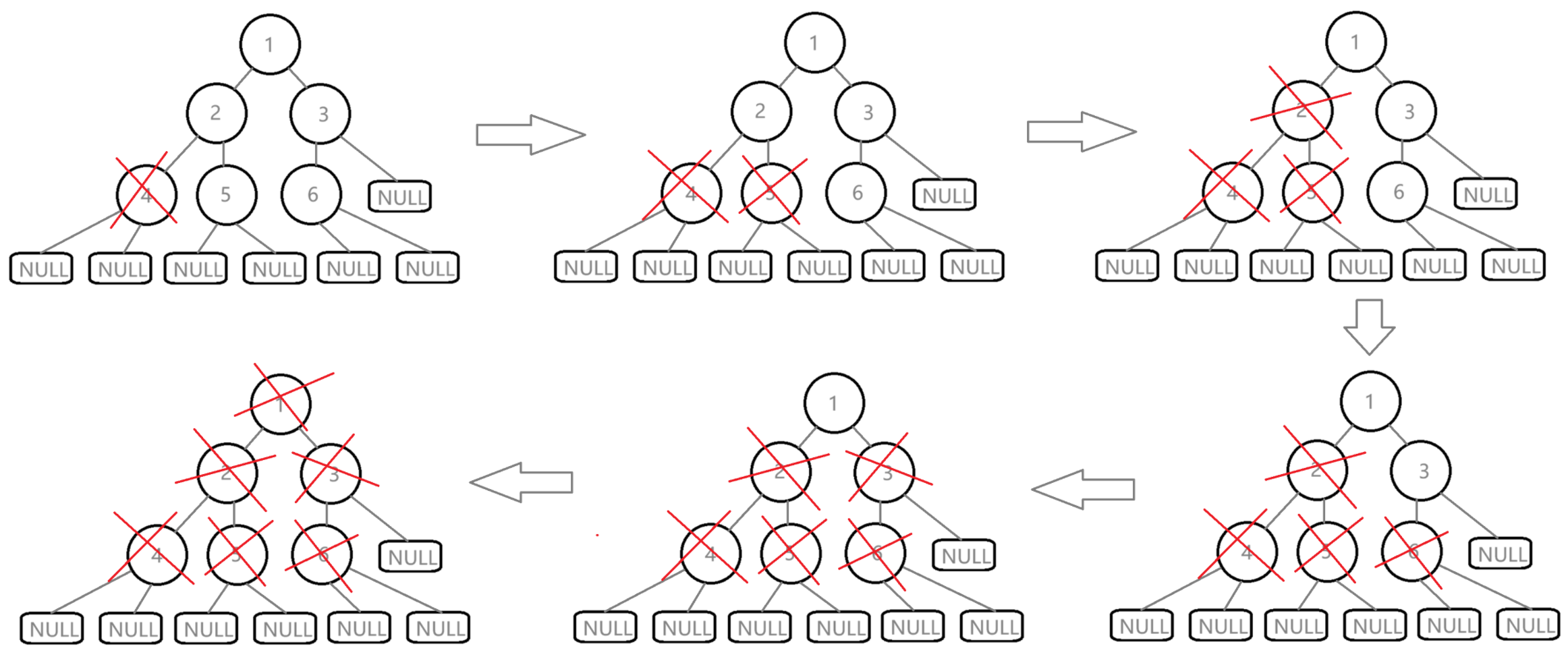
在这里插入图片描述
后序遍历free掉所有节点
代码实现:
//销毁
void BinaryTreeDestory(BTNode** proot)
{
//root为空直接返回
if (*proot == NULL)
return;
//销毁左子树
BinaryTreeDestory(&((*proot)->left));
//销毁右子树
BinaryTreeDestory(&((*proot)->right));
free(*proot);
*proot = NULL;
}执行结果:
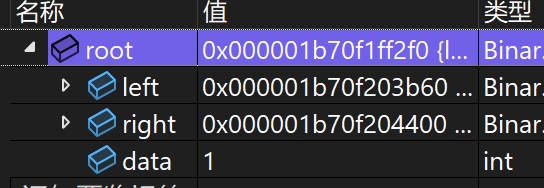
在这里插入图片描述
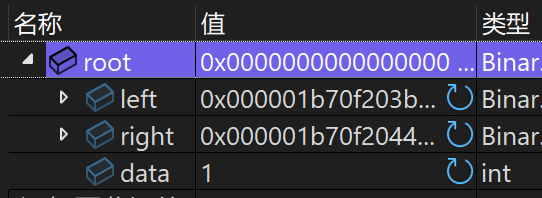
在这里插入图片描述
二、源代码
2.1 Tree.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int BTDataType;
//定义链式二叉树节点结构
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
//根据x创造节点
BTNode* BTbuyNode(BTDataType x);
//前序遍历-根左右
void preOrder(BTNode* root);
//中序遍历-左根右
void inOrder(BTNode* root);
//后续遍历-左右根
void postOrder(BTNode* root);
//二叉树节点个数
int BinaryTreeSize(BTNode* root);
//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
//二叉树第k层节点个数
int BinaryTreeLevelSize(BTNode* root, int k);
//二叉树的深度(高度)
int BinaryTreeDepth(BTNode* root);
//查找二叉树中值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
//层序遍历
void levelOrder(BTNode* root);
//判断是否为完全二叉树
bool BinaryTreeComplete(BTNode* root);
//销毁
void BinaryTreeDestory(BTNode** proot);2.2 Tree.c
#define _CRT_SECURE_NO_WARNINGS
#include"Tree.h"
#include"Queue.h"
//根据x创造节点
BTNode* BTbuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(1);
}
newnode->left = newnode->right = NULL;
newnode->data = x;
return newnode;
}
//前序遍历-根左右
void preOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL->");
return;
}
printf("%d->", root->data);
preOrder(root->left);
preOrder(root->right);
}
//中序遍历-左根右
void inOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL->");
return;
}
inOrder(root->left);
printf("%d->", root->data);
inOrder(root->right);
}
//后续遍历-左右根
void postOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL->");
return;
}
postOrder(root->left);
postOrder(root->right);
printf("%d->", root->data);
}
//二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
//二叉树第k层节点个数
int BinaryTreeLevelSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelSize(root->left, k - 1) + BinaryTreeLevelSize(root->right, k - 1);
}
//二叉树的深度(高度)
int BinaryTreeDepth(BTNode* root)
{
if (root == 0)
{
return 0;
}
int leftDep = BinaryTreeDepth(root->left);
int rightDep = BinaryTreeDepth(root->right);
return 1 + (leftDep > rightDep ? leftDep : rightDep);
}
//查找二叉树中值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* leftfind = BinaryTreeFind(root->left, x);
if (leftfind)
{
return leftfind;
}
BTNode* rightfind = BinaryTreeFind(root->right, x);
if (rightfind)
{
return rightfind;
}
return NULL;
}
//层序遍历
void levelOrder(BTNode* root)
{
if (root == NULL)
return;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* top = QueueFront(&q);
QueuePop(&q);
printf("%d ", top->data);
if (top->left)
QueuePush(&q, top->left);
if (top->right)
QueuePush(&q, top->right);
}
QueueDesTory(&q);
}
//判断是否为完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
if (root == NULL)
return;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
BTNode* top = QueueFront(&q);
while (!QueueEmpty(&q))
{
top = QueueFront(&q);
QueuePop(&q);
if (top == NULL)
{
break;
}
QueuePush(&q, top->left);
QueuePush(&q, top->right);
}
while (!QueueEmpty(&q))
{
top = QueueFront(&q);
QueuePop(&q);
if (top != NULL)
{
return false;
}
}
QueueDesTory(&q);
return true;
}
//销毁
void BinaryTreeDestory(BTNode** proot)
{
if (*proot == NULL)
return;
BinaryTreeDestory(&((*proot)->left));
BinaryTreeDestory(&((*proot)->right));
free(*proot);
*proot = NULL;
}2.3 Queue.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef struct BinaryTreeNode* QDataType;
//定义队列结点的结构
typedef struct QListNode
{
QDataType data;
struct QListNode* next;
}QListNode;
//定义队列的结构
typedef struct Queue
{
QListNode* phead;
QListNode* ptail;
//int size;
}Queue;
//队列的初始化
void QueueInit(Queue* ps);
//打印
void QueuePrint(Queue* ps);
//入队列
void QueuePush(Queue* ps, QDataType x);
//判断队列是否为空
bool QueueEmpty(Queue* ps);
//出队列
void QueuePop(Queue* ps);
//取对头数据
QDataType QueueFront(Queue* ps);
//取队尾数据
QDataType QueueBack(Queue* ps);
//队列有效元素个数
int QueueSize(Queue* ps);
//销毁
void QueueDesTory(Queue* ps);2.4 Queue.c
#define _CRT_SECURE_NO_WARNINGS
#include"Queue.h"
//队列的初始化
void QueueInit(Queue* ps)
{
assert(ps);
ps->phead = ps->ptail = NULL;
//ps->size = 0;
}
//打印
void QueuePrint(Queue* ps)
{
assert(ps);
QListNode* pcur = ps->phead;
while (pcur)
{
printf("%d", pcur->data);
pcur = pcur->next;
}
printf("\n");
}
//入队列
void QueuePush(Queue* ps, QDataType x)
{
assert(ps);
QListNode* newnode = (QListNode*)malloc(sizeof(QListNode));
if (newnode == NULL)
{
perror("malloc fail!");
exit(1);
}
newnode->data = x;
newnode->next = NULL;
if (ps->phead == NULL)
{
ps->ptail = ps->phead = newnode;
}
else
{
ps->ptail->next = newnode;
ps->ptail = newnode;
}
//ps->size++;
}
//判断队列是否为空
bool QueueEmpty(Queue* ps)
{
assert(ps);
return ps->phead == NULL;
}
//出队列
void QueuePop(Queue* ps)
{
assert(!QueueEmpty(ps));
if (ps->phead == ps->ptail)
{
ps->phead = ps->ptail = NULL;
}
else
{
QListNode* del = ps->phead;
ps->phead = ps->phead->next;
free(del);
del = NULL;
}
//ps->size--;
}
//取对头数据
QDataType QueueFront(Queue* ps)
{
assert(!QueueEmpty(ps));
return ps->phead->data;
}
//取队尾数据
QDataType QueueBack(Queue* ps)
{
assert(!QueueEmpty(ps));
return ps->ptail->data;
}
//队列有效元素个数
int QueueSize(Queue* ps)
{
assert(ps);
int size = 0;
QListNode* pcur = ps->phead;
while (pcur)
{
size++;
pcur = pcur->next;
}
return size;
//return ps->size;
}
//销毁
void QueueDesTory(Queue* ps)
{
assert(ps);
QListNode* pcur = ps->phead;
while (pcur)
{
QListNode* next = pcur->next;
free(pcur);
pcur = next;
}
ps->phead = ps->ptail = NULL;
//ps->size = 0;
}本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2026-01-13,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

