随机链表复制的终极奥秘——初学者的三步破解法

Extreme35

发布于 2025-12-23 18:28:19

1650

文章被收录于专栏：DLDL

今天我们来看一道非常经典的链表题：随机链表的复制。第一次看到这道题时，有点蒙圈。但经过一番挣扎、画图和思考，最终领悟了其中“O(1) 空间复杂度”的精妙解法。

这篇博客将完全以一个初学者的视角展开，记录我每一步的困惑、尝试和突破，希望能给你带来启发。

1. 初次读题，一脸懵圈

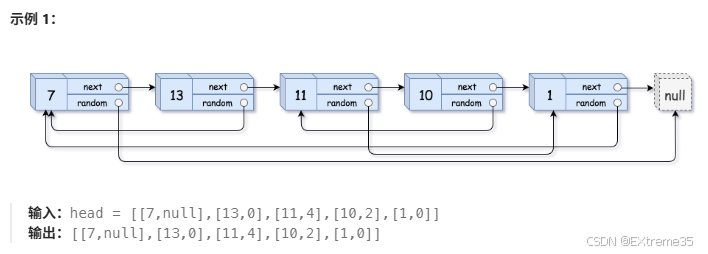
给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。深拷贝应该正好由 n 个全新节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码只接受原链表的头节点 head 作为传入参数。

当我看到题目要求：给你一个链表，除了常规的 next 指针外，每个节点还有一个 random 指针，它可能指向链表中的任意节点或 NULL。要求你深拷贝这个链表。

困难点：`random` 指针

常规链表复制：简单，遍历一次，创建新节点，把 next 指针连起来就行了。
随机链表：麻烦就在于这个 random 指针。它的指向毫无规律，就无法用常规思路去写。

为什么麻烦？

假设原链表是

\text{A} \to \text{B}

。我们创建了拷贝链表

\text{A'} \to \text{B'}

。

当我创建

\text{A'}

时，我怎么知道

\text{A'}

的 random 应该指向谁？

如果

\text{A.random} = \text{B}

，那么

\text{A'.random}

应该指向

\text{B'}

。

但当我创建

\text{A'}

时，

\text{B'}

可能还没创建！我怎么指向一个不存在的东西？

故浅拷贝不行！ 新节点必须完全独立。不能简单地让

\text{A'.random} = \text{A.random}

，因为

\text{A.random}

指向的是原链表中的节点，而不是新链表中的拷贝节点。

第一反应：画图！

画图就可以清楚地认识到：我们需要一个映射关系，来告诉我在原链表中 A 对应的拷贝是 A’。

2. 第一版尝试——用哈希表

既然需要映射关系，我立刻想到了最直接、最笨的方法：哈希表（Hash Map）。

思路：两遍遍历

第一次遍历（创建节点和映射）：
- 遍历原链表，每遇到一个原节点
Cur
，就创建一个拷贝节点
Cur'
。
- 将这对关系存入哈希表：
\text{Map}[Cur] = Cur'
。
- （这时候只创建了节点，还没连接
\text{next}
和
\text{random}
）
第二次遍历（连接指针）：
- 再次遍历原链表，每遇到一个原节点
Cur
。
- 从哈希表中取出它的拷贝节点
Cur'
。
- 设置
Cur'
的 next：
\text{Cur'.next} = \text{Map}[Cur.next]
- 设置
Cur'
的 random：
\text{Cur'.random} = \text{Map}[Cur.random]

这个方法非常有效且容易理解。时间复杂度

O(N)

（两次遍历），空间复杂度

O(N)

（哈希表存储

N

个节点）。它能解决问题，但还能继续优化吗？能不能不用额外空间，达到

O(1)

空间复杂度？

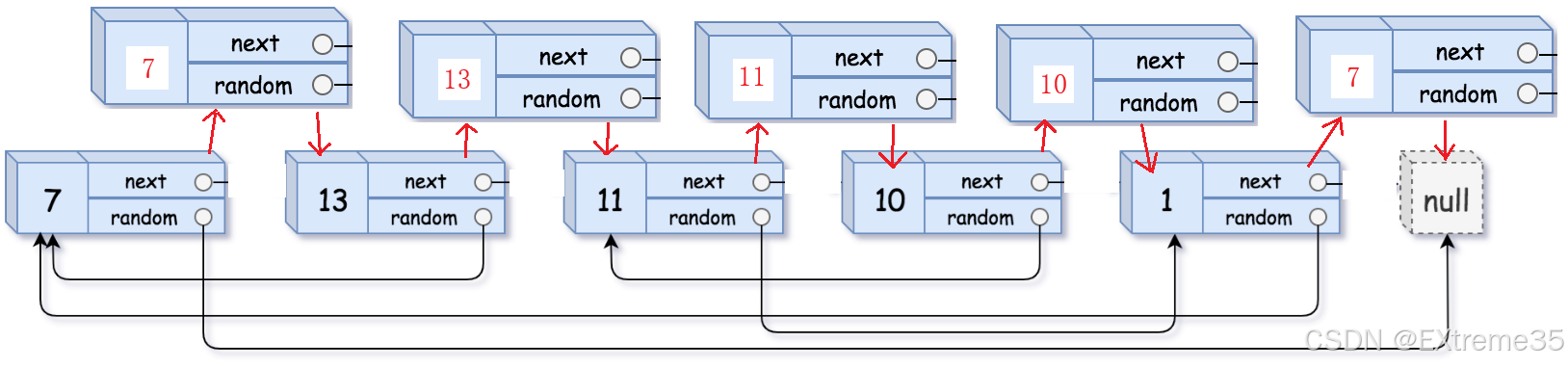
3. 灵光一闪——在原链表上做文章

我盯着链表结构图发呆，心想：既然

O(N)

空间是浪费在哈希表上，那有没有一种天然的映射，可以替代哈希表？

为什么不把拷贝节点直接插到原节点的旁边呢？

嵌入式映射

原链表：

\text{A} \to \text{B} \to \text{C} \to \text{NULL}

嵌入后：

\text{A} \to \text{A'} \to \text{B} \to \text{B'} \to \text{C} \to \text{C'} \to \text{NULL}

关键优势：

映射是天然的！ 对于任意原节点

\text{Cur}

，它的拷贝节点

\text{Cur'}

永远是

\text{Cur.next}

。

公式成立：

\text{Cur'} = \text{Cur.next}

有了这个天然的

O(1)

查找映射，我就可以进入最难的部分了！

4. 解决 random 指针——最烧脑的部分

现在，我的链表是混合的，我需要设置拷贝节点 (

\text{A'}, \text{B'}, \text{C'}

) 的

\text{random}

指针。

假设原节点

\text{A}

的

\text{random}

指向

\text{C}

。即

\text{A.random} = \text{C}

。那么，它的拷贝节点

\text{A'}

的

\text{random}

应该指向

\text{C'}

。即

\text{A'.random} = \text{C'}

。

如何找到

\text{C'}

？

第一步：从

\text{A}

找到它

\text{random}

指向的原节点

\text{C}

：

\text{cur\_random} = \text{A.random} \implies \text{C}

第二步：利用“嵌入式映射”，我们知道

\text{C'}

就在

\text{C}

的隔壁：

\text{C'} = \text{C.next}

核心公式的诞生！

\text{A'.random} = \text{A.random.next}

画图辅助写代码：

用代码来表达就是：

// 当前节点是 cur (原节点), 它的拷贝节点是 copy (cur->next)
struct Node* copy = cur->next;

if (cur->random != NULL) {
    // 假设 cur->random 指向 C，那么 C 的拷贝 C' 就在 C 的 next
    copy->random = cur->random->next;
} else {
    // 边界情况：如果原节点的 random 是 NULL，那么拷贝的 random 也是 NULL
    copy->random = NULL;
}

至此，

\text{random}

指针的问题在

O(N)

的时间复杂度下解决了！

5. 拆分链表——最后的难关

现在，我有一个完美复制了

\text{next}

和

\text{random}

的混合链表：

\text{A} \to \text{A'} \to \text{B} \to \text{B'} \to \text{C} \to \text{C'}

。

我最后的任务是：

恢复原链表：

\text{A} \to \text{B} \to \text{C}

构建新链表：

\text{A'} \to \text{B'} \to \text{C'}

同时拆分与重连

我们可以在一次遍历中完成这两件事。我们用两个指针

cur

和

copy

来分别维护原链表和新链表.

cur

负责恢复原链表的

\text{next}

：cur->next = cur->next->next (即

\text{A} \to \text{B}

)

copy

负责构建新链表的

\text{next}

：copy->next = copy->next->next (即

\text{A'} \to \text{B'}

)

6. 完整代码实现

将这三个阶段整理成一个清晰的三步走流程，并用 C 语言实现，添加详细的注释来解释每一步的思考。

struct Node* copyRandomList(struct Node* head) 
{
    if (head == NULL)
        return NULL; // 边界情况1：空链表，返回 NULL
    // --- 步骤 1: 插入拷贝节点 (建立 O(1) 映射) ---
    // 我需要一个天然的映射，代替 O(N) 的哈希表。
    // 策略：把拷贝节点插在原节点后面，即 A -> A' -> B -> B'
    struct Node* cur = head;
    while (cur != NULL) 
    {
        // 创建 A' 节点，值和 A 一样
        struct Node* copy = (struct Node*)malloc(sizeof(struct Node));
        copy->val = cur->val;
        // A' 的 next 指向 B
        copy->next = cur->next;        
        // A 的 next 指向 A'
        cur->next = copy;
        // 移动到下一个原节点 B (即 A' 的 next)
        cur = copy->next; 
    }
    // --- 步骤 2: 复制 random 指针 (利用 O(1) 映射) ---
    // 现在我们有 A -> A' -> B -> B' 的结构
    // 核心公式：A'.random = A.random->next (因为 A.random->next 就是 A.random 的拷贝节点)
    cur = head;
    while (cur != NULL) 
    {
        struct Node* copy = cur->next;
        // 边界情况2：如果原节点的 random 是 NULL
        if (cur->random != NULL) {
            // A.random 假设是 C，那么 C 的拷贝 C' 就是 C.next
            copy->random = cur->random->next;
        else 
            copy->random = NULL;
        // 移动到下一个原节点 B (即 A' 的 next)
        cur = copy->next;
    }
    // --- 步骤 3: 拆分链表 (恢复原链表结构并构建新链表) ---
    // 拆分：A -> A' -> B -> B' 变成 A -> B 和 A' -> B'
    struct Node* new_head = head->next; // 新链表的头节点 (即 A')
    cur = head;
    // 为什么要用 new_head 作为新链表的头？
    // 因为 head (A) 永远是原链表的头，它的 next (A') 永远是新链表的头。
    while (cur != NULL) 
    {
        struct Node* copy = cur->next; // 拷贝节点 (A')
        // 1. 恢复原链表的 next: A -> B
        cur->next = copy->next; 
        // 2. 构建新链表的 next: A' -> B'
        if (copy->next != NULL)
            // copy->next 此时指向 B。B 的拷贝 B' 就在 B 的 next 位置
            copy->next = copy->next->next; 
        else
            // 边界情况3：如果是最后一个拷贝节点 C'，它的 next 应该指向 NULL
            copy->next = NULL;

        // 移动到下一个原节点 B
        cur = cur->next;
    }
    // 返回新链表的头节点
    return new_head; 
}

7. 测试与验证 ✅

为了验证算法，手动构造了一个小例子，并画出每一步的链表状态：

测试用例：

\text{A} \to \text{B} \to \text{NULL}

。且

\text{A.random} = \text{B}

，

\text{B.random} = \text{A}

。

步骤一：插入拷贝节点

节点	初始状态	插入后
A	A → B A \to B A→B	A → A ′ → B A \to A' \to B A→A′→B
B	B → N U L L B \to NULL B→NULL	B → B ′ → N U L L B \to B' \to NULL B→B′→NULL
结果		A → A ′ → B → B ′ → N U L L A \to A' \to B \to B' \to NULL A→A′→B→B′→NULL

A \to B

A \to A' \to B

B

B \to NULL

B \to B' \to NULL

结果

A \to A' \to B \to B' \to NULL

步骤二：复制 random 指针

当前节点 cur \text{cur} cur	拷贝节点 copy \text{copy} copy	cur.random \text{cur.random} cur.random	copy.random \text{copy.random} copy.random 设置为	验证公式
A	A’	B	B’ ( B.next \text{B.next} B.next)	A.random.next = B.next = B’ \text{A.random.next} = \text{B.next} = \text{B'} A.random.next=B.next=B’ ✓
B	B’	A	A’ ( A.next \text{A.next} A.next)	B.random.next = A.next = A’ \text{B.random.next} = \text{A.next} = \text{A'} B.random.next=A.next=A’ ✓

\text{cur}

拷贝节点

\text{copy}

\text{cur.random}

\text{copy.random}

设置为验证公式AA’BB’ (

\text{B.next}

)

\text{A.random.next} = \text{B.next} = \text{B'}

✓BB’AA’ (

\text{A.next}

)

\text{B.random.next} = \text{A.next} = \text{A'}

✓

步骤三：拆分链表

当前节点 cur \text{cur} cur	拷贝节点 copy \text{copy} copy	恢复 cur.next \text{cur.next} cur.next	构建 copy.next \text{copy.next} copy.next
A	A’	A.next → B \text{A.next} \to \text{B} A.next→B	A’.next → B’ \text{A'.next} \to \text{B'} A’.next→B’
B	B’	B.next → NULL \text{B.next} \to \text{NULL} B.next→NULL	B’.next → NULL \text{B'.next} \to \text{NULL} B’.next→NULL

\text{cur}

拷贝节点

\text{copy}

恢复

\text{cur.next}

构建

\text{copy.next}

AA’

\text{A.next} \to \text{B}

\text{A'.next} \to \text{B'}

BB’

\text{B.next} \to \text{NULL}

\text{B'.next} \to \text{NULL}

最终结果：

原链表：

\text{A} \to \text{B} \to \text{NULL}

（结构已恢复）

新链表：

\text{A'} \to \text{B'} \to \text{NULL}

，且

\text{A'.random} \to \text{B'}

，

\text{B'.random} \to \text{A'}

（复制成功）

8. 总结

三步法的核心思想：

插入（Embed）：建立原节点-拷贝节点的物理相邻关系。这用

O(1)

的时间替代了

O(N)

空间的哈希表映射。这是从

O(N)

空间到

O(1)

空间的关键一步。

复制（Utilize）：利用这种相邻关系，通过 cur->random->next 的公式，快速定位

\text{random}

对应的拷贝节点.

拆分（Separate）：优雅地将混合链表分离，边拆分边重连，同时恢复原链表，构建新链表。

建议

遇到难题，先画图！ 相信我，画图思考比干想代码有效 100 倍。
从最简单的情况开始。 比如，先只考虑

\text{next}

指针，再引入

\text{random}

指针。

多问自己“能不能更好？” 如果我一开始满足于哈希表

O(N)

的解法，就不会去探索这个

O(1)

空间的精妙技巧了。

希望我的这份“初学者思考路径”能帮助你彻底理解并掌握这道随机链表的复制问题！

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-12-23，如有侵权请联系 cloudcommunity@tencent.com 删除

text

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体同步曝光计划，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度