高阶数据结构-并查集

一、并查集原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组的集合合并。在此过程中要反复用到查询某一个元素归属那一个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find-set)。

举个例子，比如某公司今年春招全国共招生10人，重庆招4人，成都招3人，贵州招3人，10个人来自不同的学校，起先他们互不相识，每个学生都是一个独立的小团体，现给这些新人员工进行编号：{0，1，2，3，4，5，6，7，8，9}；用以下数组存储每个小团体，数组中的数字代表：该集体中具有成员的个数。(符号下会解释)。

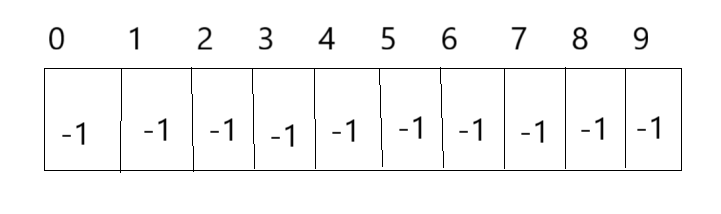
这里有两点需要注意：

1、和堆相似，用下标表示关系

2、下标关系是双亲表示法(存储父节点索引(下标))

继续看例子，此时我们的新员工要去公司上班了，每个地方的学生自发组织成小分队一起前往公司，于是就有了一下小分队：重庆队s1={0，6，7，8}，成都队s2={1，4，9}，武汉队s3={2，3，5}，10个人形成了3个小团体。假设由三个群主0，1，2担任队长，负责大家的出行。

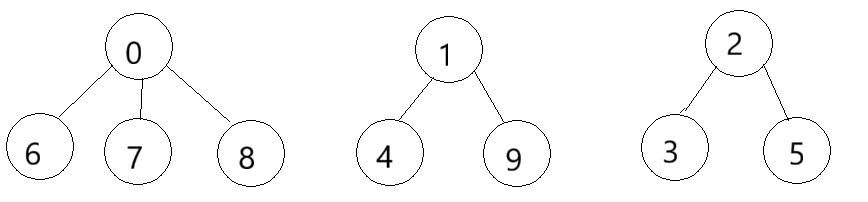
树形结构展示

并查集的本质就是森林，森林就是很多棵树

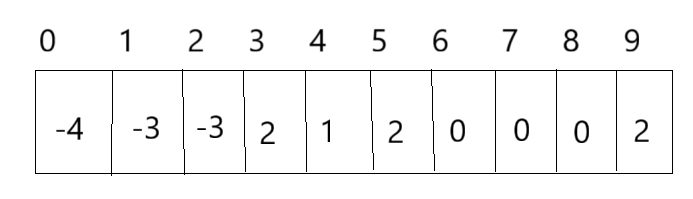
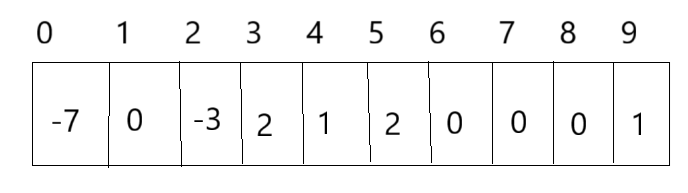
森林指针数组展示

指针数组有两个特点：

1、一个位置的值是负数，那它就是树的根，这个负数的绝对值就是这棵树节点的个数

2、一个位置的值是正数，那它就是双亲的下标

在后面的相处共事中我们的重庆队的队长和成都队的队长看对眼了，他们也就成了男女朋友关系，自然重庆队的队长会把成都队的队长介绍给自己的同乡，成都队的队长也是如此，所以他们个人有了新的关系，由此可以对两个团队进行合并。

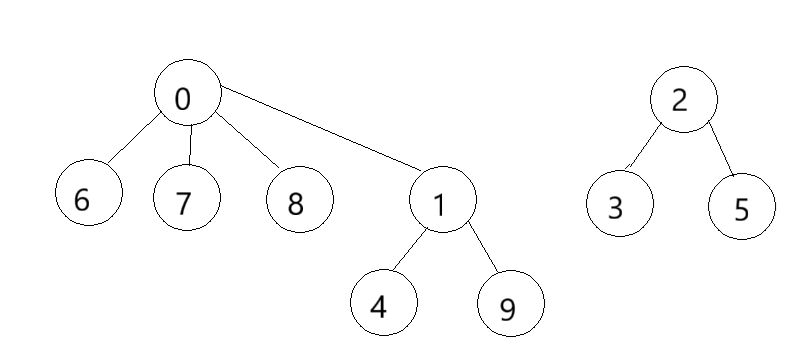
我们通过双亲表示法找到根，然后再合并

二、并查集的实现

由于和堆差不多用数组模拟，所以先在UnionFindSet类中定义一个vector<int> _ufs；的私有变量

1、构造函数

由于初始状态每个元素都是一个集合，所以初始化为-1，通过初始化列表调用vector的构造，这里匹配的是vector(size_type n,const value_type& val)

UnionFindSet(size_t n)
		:_ufs(n, -1)
	{ }

2、找根函数

在进行合并之前我们需要判断两个要合并的元素是不是属于同一个集合的，所以找根函数便发挥了作用

具体原理：由于双亲表示法，我们以要找根的元素当作下标访问_ufs数组，如果该值小于0，则说明它就是根，返回即可；如果该值大于0，则继续以该值为下标访问_ufs数组，重复这个判断行为，最终返回根

int FindRoot(int x)//找根
	{
		int parent = x;
		while (_ufs[parent] >= 0)
		{
			parent = _ufs[parent];
		}

		return parent;
	}

3、合并函数

我们已经有了上面的找根函数，可以轻松完成找根工作，此时我们还需要判断一下，如果两个合并元素的根相同，则不合并。而且对于合并的根并没有做强制的要求，合并的两个元素谁当根都可以。

合并具体操作：将被合并根的值，也就是被合并的集合个数+=另一个合并的根，然后将被合并根的值修改为另一个合并的根

void Union(int x1,int x2)//并
	{
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		//属于同一个集合没必要合并
		if(root1 == root2) return;

		//小的做根
		if (root1 > root2) swap(root1, root2);

		_ufs[root1] += _ufs[root2];
		_ufs[root2] = root1;
		
	}

这里的小的做根看自己的需要

4、判断两个元素是否属于同一集合

通过找根函数，返回比较根是否相等，相等则true，不等则false

bool InSet(int x1,int x2)
	{ 
		return FindRoot(x1) == FindRoot(x2);
	}

5、统计集合的数量

由于根所存储的值为负数，所以只需遍历_ufs数组即可

size_t SetSize()
	{
		size_t size = 0;
		for (size_t i = 0; i < _ufs.size(); i++)
		{
			if (_ufs[i] < 0) ++size;
		}

		return size;
	}

6、完整类结构

class UnionFindSet
{
public:
	UnionFindSet(size_t n)
		:_ufs(n, -1)
	{ }

	void Union(int x1,int x2)//并
	{
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		//属于同一个集合没必要合并
		if(root1 == root2) return;

		//小的做根
		if (root1 > root2) swap(root1, root2);

		_ufs[root1] += _ufs[root2];
		_ufs[root2] = root1;
		
	}

	int FindRoot(int x)//找根
	{
		int parent = x;
		while (_ufs[parent] >= 0)
		{
			parent = _ufs[parent];
		}

		return parent;
	}

	bool InSet(int x1,int x2)
	{ 
		return FindRoot(x1) == FindRoot(x2);
	}

	size_t SetSize()
	{
		size_t size = 0;
		for (size_t i = 0; i < _ufs.size(); i++)
		{
			if (_ufs[i] < 0) ++size;
		}

		return size;
	}

private:
	vector<int> _ufs;
};

三、总结和并查集的实践

回顾全文，并查集作为处理 “动态连通性” 问题的经典数据结构，其核心魅力在于用极简的数组模拟森林，通过高效操作实现集合的管理与查询。从原理上看，它以 “双亲表示法” 为基础 —— 初始时每个元素自成集合（数组值为 - 1），根节点的负数值绝对值代表集合大小，非根节点的正数值指向父节点，清晰构建了元素间的从属关系；就像文中 10 名新员工从 “各自为营” 到 “按地域组队”，再到 “跨队合并” 的过程，生动体现了并查集 “从森林到单树（或少数树）” 的演变逻辑。​

在实现层面，并查集的核心围绕三大操作展开：FindRoot追溯根节点确定集合归属，Union将不同集合按 “小根合并到大根” 的原则整合，InSet通过对比根节点判断元素是否同属一集，再辅以SetSize统计集合总数，整个类结构简洁且逻辑闭环。而路径压缩与按大小 / 秩合并的优化，更是将操作效率推向 “近常数时间”，让它在大数据场景下依然保持出色性能，这也是其能成为算法领域 “常青树” 的关键。​

从应用角度看，并查集的价值远超理论 —— 它既能在图论中支撑 Kruskal 算法求最小生成树（避免环的产生）、统计连通分量，也能解决实际中的 “亲戚关系验证”“网络节点连通判断”“重叠区间合并” 等问题，真正实现了 “数据结构服务于实际需求”。​

最后想说，学习并查集的意义不仅在于掌握一种工具，更在于理解 “用简单结构解决复杂问题” 的思维：通过抽象元素关系（用数组代森林）、优化操作路径（路径压缩）、平衡结构形态（按大小合并），让看似繁琐的 “集合管理” 变得高效可控。无论是算法竞赛还是工程开发，这种 “化繁为简” 的思路，都将成为解决问题的重要助力。

这里是两道力扣题可以利用刚写好的简易版并查集去尝试解决一下。

547. 省份数量 - 力扣（LeetCode）

990. 等式方程的可满足性 - 力扣（LeetCode）