【强化学习】深入理解：PPO（Proximal Policy Optimization） 和 TRPO（Trust Region Policy Optimization） 的本质区别

📢本篇文章是博主强化学习（RL）领域学习时，用于个人学习、研究或者欣赏使用，并基于博主对相关等领域的一些理解而记录的学习摘录和笔记，若有不当和侵权之处，指出后将会立即改正，还望谅解。文章分类在👉强化学习专栏： 【强化学习】- 【强化学习进阶】（2）---《深入理解：PPO 和 TRPO 的本质区别》

【强化学习】深入理解：PPO 和 TRPO 的本质区别

1. 引言

PPO（Proximal Policy Optimization）算法是 OpenAI 提出的强化学习算法，旨在改进 TRPO（Trust Region Policy Optimization）的性能，特别是在计算效率和实现复杂度上，当前是强化学习领域中极具影响力的方法之一，因其兼具稳定性、效率和实现简洁性而被广泛应用于机器人控制、游戏AI等多个场景。它通过限制策略更新的幅度，有效解决了传统策略梯度方法不稳定的问题，成为深度强化学习的代表算法。PPO不仅推动了强化学习在实际应用中的落地，也为后续算法的研究提供了坚实基础，具有重要的理论与实践意义。

PPO（Proximal Policy Optimization） 和 TRPO（Trust Region Policy Optimization） 的最本质的区别是什么呢？ 下面先给出结论：

2. PPO和TRPO本质区别

归根结底在于 如何控制策略更新的幅度 以及 计算复杂度。

1. 控制策略更新的方式：

• TRPO 通过 KL散度约束 来控制策略更新的幅度。它通过计算自然梯度和使用Fisher信息矩阵，确保每次策略更新不会超过一个信任域，从而避免了策略的过度更新。TRPO的目标是最大化回报的同时，确保新策略与旧策略之间的差异保持在一个可接受的范围内。 TRPO的控制策略更新的方式是 严格的、精确的，它直接对策略的更新进行严格约束，确保每一步更新的KL散度不超过设定的阈值。这种方法避免了策略更新的过度波动，提高了稳定性。
• PPO 则通过 裁剪目标函数（clipping）来实现对策略更新的控制。裁剪操作通过限制比率

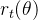
r_t(\theta)

超过一个预设的范围（通常是

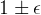
1 \pm \epsilon

），从而避免更新过大或过小。这是一种 简化的、间接的 控制方法，不需要像TRPO那样显式计算KL散度。 PPO的更新控制方法相对 松散且高效，它通过裁剪目标函数来防止策略过度变化，而不需要计算复杂的二阶导数或优化约束。裁剪方法不仅可以有效控制更新幅度，还能降低计算复杂度。

2. 计算复杂度：

• TRPO 需要计算 Fisher信息矩阵的逆 和 自然梯度，涉及二阶导数的计算，这使得它的计算复杂度相对较高，特别是在高维的强化学习问题中，TRPO的计算成本可能非常大。
• PPO 则通过裁剪目标函数，使用 一阶梯度 来优化策略，避免了计算二阶导数和Fisher信息矩阵的需求。这使得PPO的计算复杂度大大降低，适合在大规模问题中应用，并且容易实现。

3.具体分析

上述结论给出了答案，其实PPO和TRPO算法最大的不同就是在如何控制策略更新的幅度，因为采取的控制方式不同，使得PPO的计算复杂度远远少于TRPO，更适合于应用。下面给出具体的分析：

3.1优化目标和约束

首先针对于优化目标和约束：

TRPO：

目标函数：TRPO的优化目标是最大化回报，同时保证新策略与旧策略之间的变化在一个信任域（trust region）内。TRPO通过KL散度约束来确保策略更新不会偏离原策略太多。

\max_{\theta} \mathbb{E} \left[ \frac{\pi_{\theta}(a|s)}{\pi_{\theta_{\text{old}}}(a|s)} A(s, a) \right]

其中，

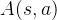
A(s, a)

是优势函数。

KL散度约束：TRPO直接在优化过程中对KL散度进行约束，确保新旧策略之间的差异在一个预设的阈值内。这是通过自然梯度和二阶导数来实现的。

约束形式为：

\mathbb{E} \left[ \text{KL}(\pi_{\theta_{\text{old}}} || \pi_{\theta}) \right] \leq \delta

这意味着TRPO显式地控制了每次更新的幅度，避免策略发生过大的变化。

如果用惩罚因子替代约束条件，TRPO优化问题可以表述为：

\underset{\theta}{\operatorname*{\operatorname*{maximize}}}\hat{\mathbb{E}}_t\left[\frac{\pi_\theta(a_t\mid s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t\mid s_t)}\hat{A}_t-\beta\operatorname{KL}[\pi_{\theta_{\mathrm{old}}}(\cdot\mid s_t),\pi_\theta(\cdot\mid s_t)]\right]

PPO：

目标函数：PPO的优化目标与TRPO类似，也是希望最大化回报并控制策略更新。然而，PPO使用的是裁剪目标函数（clipped objective）来近似解决TRPO中的KL散度约束。

\mathcal{L}(\theta) = \mathbb{E}_t \left[ \min \left( r_t(\theta) A_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) A_t \right) \right]

其中，

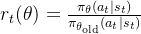
r_t(\theta)=\frac{\pi_\theta(a_t\mid s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t\mid s_t)}

是新的策略概率与旧策略概率的比值，

\epsilon

是一个小常数，通常为0.2。

裁剪方法：PPO并不直接计算KL散度，而是通过裁剪目标函数来间接控制策略更新的幅度。当比率

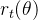
r_t(\theta)

超过某个范围时（通常是 1 ± ε），PPO就会裁剪它，避免更新过大。裁剪方法简单有效，避免了TRPO中需要计算复杂的KL散度的情况。

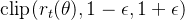
\text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon)

PPO优化问题可以表述为（为了更好理解）：

\hat{\mathbb{E}}_t\left[\min(\frac{\pi_\theta(a_t\mid s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t\mid s_t)}\hat{A}_t,\mathrm{clip}(r_t(\theta),1-\epsilon,1+\epsilon)\hat{A}_t)\right]

这里我们便可以发现他们两者之间采用控制策略更新幅度方法的不同，一个采用自然梯度（KL散度），一个采用裁剪；接下来我们继续分析这两种方法的区别和带来的效果.

3.2自然梯度 vs 裁剪

TRPO：

自然梯度：TRPO通过计算自然梯度进行优化。自然梯度方法利用二阶导数信息（通过Fisher信息矩阵近似海森矩阵），调整梯度方向，并控制更新步长。TRPO使用KL散度约束来确保每次策略更新都不会偏离太多，这需要计算复杂的二阶导数信息。

二阶导数（通过Fisher信息矩阵近似海森矩阵）与KL散度之间的关系是TRPO算法的核心之一。为了理解它们之间的联系，我们现在逐步分析每个概念及其如何协同工作以优化策略。

3.2.1.KL散度（Kullback-Leibler Divergence）

KL散度是衡量两个概率分布之间差异的度量，尤其用于描述新旧策略之间的“相似度”或“差异”。在TRPO中，KL散度用来确保策略的更新不会偏离原策略过多，以避免在策略优化过程中出现不稳定的情况。

KL散度的定义为：

\text{KL}(\pi_{\theta_{\text{old}}} || \pi_{\theta}) = \mathbb{E}_{s \sim \rho_{\theta_{\text{old}}}} \left[ \log \frac{\pi_{\theta_{\text{old}}}(a|s)}{\pi_{\theta}(a|s)} \right]

其中：

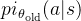
pi_{\theta_{\text{old}}}(a|s)

是旧策略的概率分布。

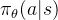
\pi_{\theta}(a|s)

是新策略的概率分布。

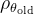
\rho_{\theta_{\text{old}}}

是旧策略下的状态分布。

KL散度的本质是度量新旧策略之间的差异。TRPO的目标是限制KL散度不超过一个预设的阈值（通常是一个很小的正数），从而控制策略更新的幅度，确保优化过程中的稳定性。

3.2.2.自然梯度和Fisher信息矩阵

TRPO使用自然梯度方法来优化策略。自然梯度的一个重要特性是考虑了目标函数的几何结构，而不仅仅是梯度的大小和方向。通过引入二阶信息（Fisher信息矩阵），自然梯度方法能够更精确地指导策略的更新。

Fisher信息矩阵 F是目标函数的二阶导数的近似，通常用于修正梯度，使得梯度更新不依赖于参数空间的坐标系。Fisher信息矩阵的定义是：

F = \mathbb{E} \left[ \nabla_{\theta} \log \pi_{\theta}(a|s) \nabla_{\theta} \log \pi_{\theta}(a|s)^T \right]

其中：

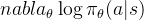
nabla_{\theta} \log \pi_{\theta}(a|s)

是策略对数的梯度。

Fisher信息矩阵度量了策略参数空间的曲率，类似于海森矩阵（目标函数的二阶导数）。自然梯度方法通过乘以

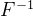
F^{-1}

来调整梯度，使得更新步长和方向更加合适，从而避免了简单梯度下降法可能遇到的过大或过小的更新步长问题。

3.3.3KL散度约束的推导过程

TRPO的优化目标是最大化目标函数，同时满足KL散度约束。为了有效地进行优化，TRPO会对KL散度约束进行二阶近似。这个二阶近似与Fisher信息矩阵密切相关。

假设我们在当前位置

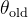
\theta_{\text{old}}

附近进行小范围的更新，可以通过泰勒展开近似KL散度：

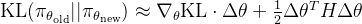
\text{KL}(\pi_{\theta_{\text{old}}} || \pi_{\theta_{\text{new}}}) \approx \nabla_{\theta} \text{KL} \cdot \Delta \theta + \frac{1}{2} \Delta \theta^T H \Delta \theta

其中：

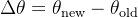
\Delta \theta = \theta_{\text{new}} - \theta_{\text{old}}

是参数的变化。

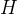
H

是海森矩阵（Hessian matrix），或者在TRPO中近似为Fisher信息矩阵。

这个泰勒展开公式说明了KL散度的变化是由梯度项（一阶导数）和海森矩阵项（二阶导数）共同决定的。为了控制KL散度，TRPO通过对Fisher信息矩阵进行近似来确保每次更新的步长和方向在合理的范围内。

3.3.4 Fisher信息矩阵和KL散度的结合

Fisher信息矩阵提供了目标函数的局部几何信息，即在当前位置的曲率，它度量了每个策略参数对最终回报的影响程度。这个矩阵能够帮助TRPO调整梯度方向，并且防止在优化过程中出现过大的更新。 在TRPO中，Fisher信息矩阵的作用是对梯度进行修正，使得每次更新都更加稳定。Fisher矩阵本质上是KL散度的二阶导数的近似，因此它能准确反映新旧策略之间差异的变化。

TRPO通过自然梯度方法计算更新步长，利用二阶信息（Fisher信息矩阵的近似）来限制策略更新。 简单来说：TRPO采用KL散度约束用来确保策略不发生剧烈变化，那么计算KL散度需要通过二阶导数（海森矩阵），而Fisher信息矩阵便是海森矩阵的近似，帮助TRPO合理地调整每次策略更新的幅度。所以Fisher信息矩阵是用来求解KL散度，二者结合，确保了TRPO在优化过程中既能高效收敛，又能保持策略的稳定性。

计算复杂度：由于需要计算和反向传播Fisher信息矩阵，TRPO的计算复杂度较高，尤其在高维空间中。

PPO：

裁剪方法：PPO使用一阶梯度进行优化，计算相对简单。它通过裁剪（clipping）目标函数来限制策略更新的幅度，而不需要计算二阶导数或KL散度。裁剪方法使得PPO的实现更加简洁和高效，且计算复杂度较低。

计算复杂度：PPO的计算复杂度低于TRPO，因为它不需要计算Fisher信息矩阵，只涉及一阶梯度信息。

介绍来介绍，采用KL散度和裁剪控制策略更新的幅度带来的效果。

3.3 计算稳定性和收敛性

TRPO：

高计算稳定性：TRPO通过KL散度约束和自然梯度的方法，保证了每次策略更新的稳定性。它通过严格的信任域控制，确保策略更新在可接受范围内，从而避免过度更新导致的性能下降。 收敛速度较慢：由于计算复杂度较高，TRPO的收敛速度较慢，尤其是在大规模问题中。

PPO：

更高效的计算稳定性：PPO通过裁剪目标函数来避免策略更新过大，因此即使没有KL散度约束，也能保持优化的稳定性。PPO算法通常比TRPO更快、更高效。 收敛速度较快：由于算法相对简单且计算复杂度低，PPO通常具有更快的收敛速度，尤其在实际应用中表现更为优异。

3.4实现复杂度

TRPO：

实现复杂：TRPO需要计算自然梯度，并且需要计算Fisher信息矩阵的逆。这个过程涉及高阶的计算，特别是高维度时计算量大，且需要对矩阵进行反向传播和求逆，导致实现复杂度较高。

PPO：

实现简单：PPO的核心在于裁剪目标函数，使用标准的一阶梯度下降方法来优化。由于不需要计算二阶导数，也不需要计算KL散度，PPO的实现相对简洁，适合快速开发和实验。

4.补充Fisher信息矩阵

在TRPO（Trust Region Policy Optimization）算法中，二阶导数的海森矩阵起着至关重要的作用，主要用于在策略优化中确保“信任域”的约束。TRPO的核心目标是使得策略在每次更新时不会过度变化，因此它使用**自然梯度**方法来更新策略，并通过**Fisher信息矩阵**来近似海森矩阵，限制策略更新的幅度。

下面是详细的推理过程，解释TRPO是如何使用二阶导数的海森矩阵的。

4.1目标函数和约束

目标：TRPO的优化目标是最大化策略的期望回报，同时保持新旧策略之间的差异在一个可接受的范围内（即不超过一个信任域）。具体来说，TRPO的目标函数可以表示为：

\max_{\theta} \mathbb{E} \left[ \frac{\pi_{\theta}(a|s)}{\pi_{\theta_{old}}(a|s)} A(s, a) \right]

约束：为了避免策略更新过大，TRPO引入了一个**KL散度**约束，确保新旧策略之间的差异不超过一个预设的阈值：

\mathbb{E} \left[ \text{KL}(\pi_{\theta_{old}} || \pi_{\theta}) \right] \leq \delta

4.2自然梯度和海森矩阵的引入

在TRPO中，**自然梯度**是优化过程中的核心，目的是根据策略的几何结构调整梯度更新。自然梯度并不是简单地使用梯度，而是通过二阶信息对梯度进行修正，以提高更新效率和稳定性。自然梯度的定义为：

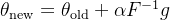
\theta_{\text{new}} = \theta_{\text{old}} + \alpha F^{-1} g

其中：

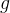
g

是普通的梯度

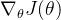
\nabla_{\theta} J(\theta)

。

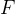
F

是Fisher信息矩阵，用来近似海森矩阵。

Fisher信息矩阵的计算是基于一阶导数的，但它通过对一阶导数的期望来反映二阶信息。因此，Fisher信息矩阵的计算涉及对似然函数的对数求一阶导数，再对一阶导数的期望进行计算。

对于参数

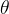
\theta

，Fisher信息矩阵定义为：

F = \mathbb{E}\left[ \left( \frac{\partial}{\partial \theta} \log p(x; \theta) \right)^2 \right]

其中，

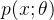
p(x; \theta)

是数据的似然函数。

这个式子表示了对对数似然函数的一阶导数的平方期望值，而不是直接涉及二阶导数。换句话说，Fisher信息矩阵通过度量一阶导数的变化来提供有关二阶性质的信息（例如，数据中参数的精确度或不确定性）。因此，Fisher信息矩阵的计算并不需要计算二阶导数，只需要计算一阶导数并取期望。

Fisher信息矩阵能够捕捉到策略空间的几何形状，从而确保更新过程的稳定性和高效性。具体来说，Fisher信息矩阵

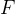
F

也可表示为：

F = \mathbb{E} \left[ \nabla_{\theta} \log \pi_{\theta}(a|s) \nabla_{\theta} \log \pi_{\theta}(a|s)^T \right]

这是一个近似的海森矩阵，描述了策略的局部曲率。

4.3KL散度约束与自然梯度结合

在TRPO中，我们希望在优化过程中限制KL散度，使得新旧策略之间的差异保持在信任域内。为此，我们需要确保在每一步更新时，策略不会改变得过多。

为了求解带有KL散度约束的优化问题，我们通过使用**自然梯度**来更新参数。更新步骤为：

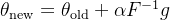
\theta_{\text{new}} = \theta_{\text{old}} + \alpha F^{-1} g

为了保持KL散度约束，我们需要对梯度进行修正。通过自然梯度的方式，我们在优化时考虑了Fisher信息矩阵的影响，从而更精确地控制了每次更新的幅度和方向。

4.4二阶导数的应用

Fisher信息矩阵实际上就是通过计算一阶导数来近似目标函数的海森矩阵。具体而言，Fisher信息矩阵的定义基于对策略对数的梯度的期望，它涉及到二阶导数的信息。海森矩阵本质上是目标函数的二阶导数，而Fisher信息矩阵是这个二阶导数的近似。

因此，TRPO算法使用自然梯度的核心原因是利用了二阶导数的信息，从而使得优化过程能够在“信任域”内进行，并避免策略更新过大或过小，确保算法的稳定性。

TRPO使用二阶导数信息（通过Fisher信息矩阵近似海森矩阵）来进行自然梯度优化。二阶导数帮助算法更准确地调整更新步长，避免更新过大或过小的问题，从而提高了优化的效率和稳定性。通过自然梯度方法和KL散度约束的结合，TRPO能够在保证策略更新稳定性的同时，达到更快的收敛速度。

5. 适用场景

TRPO：

适用于复杂问题：由于TRPO能够在严格的信任域内进行优化，它适合于需要精确控制更新步骤的高复杂度问题，尤其是在高维的策略空间中。

PPO：

适用于大规模和实时训练：由于PPO的计算复杂度较低，它适用于需要快速训练的场景，尤其在大规模应用（如视频游戏、机器人控制等）中表现较好。

6. 总结对比

7.结论

TRPO适用于需要精确控制策略更新的复杂问题，特别是在需要稳定性和高精度的任务中，如机器人控制和某些高维强化学习任务。 PPO则是一个更简洁、高效的算法，广泛适用于大规模应用和快速原型设计，尤其是在计算资源有限的情况下，PPO表现出色。

参考文献：

Proximal Policy Optimization Algorithms

Trust Region Policy Optimization

更多强化学习文章，请前往：【强化学习（RL）】专栏