快马加鞭送荔枝！用 Python 找深圳到西安的最快路线？Dijkstra 算法安排上！

原创

你好我是大河

修改于 2025-06-25 07:49:27

26700

代码可运行

运行总次数：0

代码可运行

print("点赞+评论+收藏 = 以后吃的荔枝都新鲜！")

你有没有遇到过这种情况：比如你要从一个城市出发去另一个城市，中间有很多条路可选，但你想找出“最快”或者“最省钱”的那一条？

今天我们就来解决一个实际问题：从深圳出发，怎么走才能最快到达西安？

我们手头有一个城市之间的连接图，每个城市之间都有运输时间（单位是小时）。我们的任务就是在这张图中，找到一条从深圳到西安耗时最短 的路线。

思路简单整理一下

这个问题其实就是一个典型的 最短路径问题 。我们可以把它想象成地图上的点和线：

每个城市是一个节点；
城市之间的交通线路是一条边；
边上标注的是运输时间。

要找最短路径，最常用的方法之一就是 Dijkstra 算法 。它的核心思想就是：

“我从起点出发，一步步探索所有可能的方向，每次只挑当前距离最近的城市继续探索。”

听起来是不是有点像导航软件的工作原理？

🛠具体怎么做的？

1. 把城市数据结构准备好： 我们用了一个字典 city_graph 来表示各个城市之间的连接关系和时间。

2. 实现 Dijkstra 算法： 使用了优先队列（Python 的 heapq）来优化查找过程，这样效率更高。

3. 输出结果：

最短运输时间是多少？
路径经过哪些城市？

4.可视化展示最优路径： 用 networkx 和 matplotlib 把整个图画出来，并且把最优路径标红显示。

💻 展示代码 ↓

import heapq
import matplotlib.pyplot as plt
import networkx as nx

plt.rcParams['font.sans-serif'] = ['JingDongLangZhengTi']  # 使用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False    # 解决负号 '-' 显示为方块的问题```


def dijkstra(graph, start, end):
    # 初始化距离表和前驱节点表
    distances = {node: float('inf') for node in graph}
    previous_nodes = {node: None for node in graph}
    distances[start] = 0

    # 使用优先队列维护待访问节点
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_node = heapq.heappop(priority_queue)

        # 如果当前节点已处理过，跳过
        if current_distance > distances[current_node]:
            continue

        # 遍历相邻节点
        for neighbor, weight in graph[current_node].items():
            distance = current_distance + weight

            # 如果找到更短路径，更新距离和前驱
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                previous_nodes[neighbor] = current_node
                heapq.heappush(priority_queue, (distance, neighbor))

    # 构建最短路径
    path = []
    current = end
    while current:
        path.append(current)
        current = previous_nodes[current]
    path.reverse()

    return distances[end], path


# 城市图定义
city_graph = {
    '深圳': {'广州': 1.5, '东莞': 1.0},
    '广州': {'深圳': 1.5, '韶关': 2.5, '长沙': 5.5},
    '东莞': {'深圳': 1.0, '惠州': 1.2},
    '惠州': {'东莞': 1.2, '武汉': 8.0},
    '韶关': {'广州': 2.5, '长沙': 4.0},
    '长沙': {'韶关': 4.0, '武汉': 3.0, '郑州': 8.0},
    '武汉': {'惠州': 8.0, '长沙': 3.0, '郑州': 4.5, '西安': 10.0},
    '郑州': {'长沙': 8.0, '武汉': 4.5, '洛阳': 2.0},
    '洛阳': {'郑州': 2.0, '西安': 5.0},
    '西安': {'武汉': 10.0, '洛阳': 5.0}
}

# 运行算法
total_time, shortest_path = dijkstra(city_graph, '深圳', '西安')
print(f"最短运输时间：{total_time:.2f} 小时")
print(f"最优路径：{' → '.join(shortest_path)}")

# 绘制图并突出显示最优路径
G = nx.DiGraph()

# 添加所有边
for src, neighbors in city_graph.items():
    for dst, weight in neighbors.items():
        G.add_edge(src, dst, weight=weight)

# 获取最优路径中的边
path_edges = list(zip(shortest_path, shortest_path[1:]))

# 设置布局
pos = nx.spring_layout(G, seed=42)

# 绘制所有节点和边
plt.figure(figsize=(12, 8))
nx.draw_networkx_nodes(G, pos, node_size=600, node_color='lightblue')
nx.draw_networkx_edges(G, pos, edgelist=G.edges(), arrowstyle='->', arrowsize=15)
nx.draw_networkx_labels(G, pos, font_size=12, font_weight='bold')

# 绘制最优路径边
nx.draw_networkx_edges(G, pos, edgelist=path_edges, edge_color='red', width=2.0, arrowstyle='->', arrowsize=20)

# 显示权重
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)

plt.title("深圳到西安的最优路径（红色箭头为路径）", fontsize=16)
plt.axis('off')
plt.tight_layout()
plt.savefig("shortest_path.png")

💡 运行结果

/Users/allen/PycharmProjects/myPythonCode/venv/bin/python /Users/allen/PycharmProjects/myPythonCode/2506/lizhi.py 
最短运输时间：20.00 小时
最优路径：深圳 → 广州 → 长沙 → 武汉 → 西安

Process finished with exit code 0

最佳运输路径

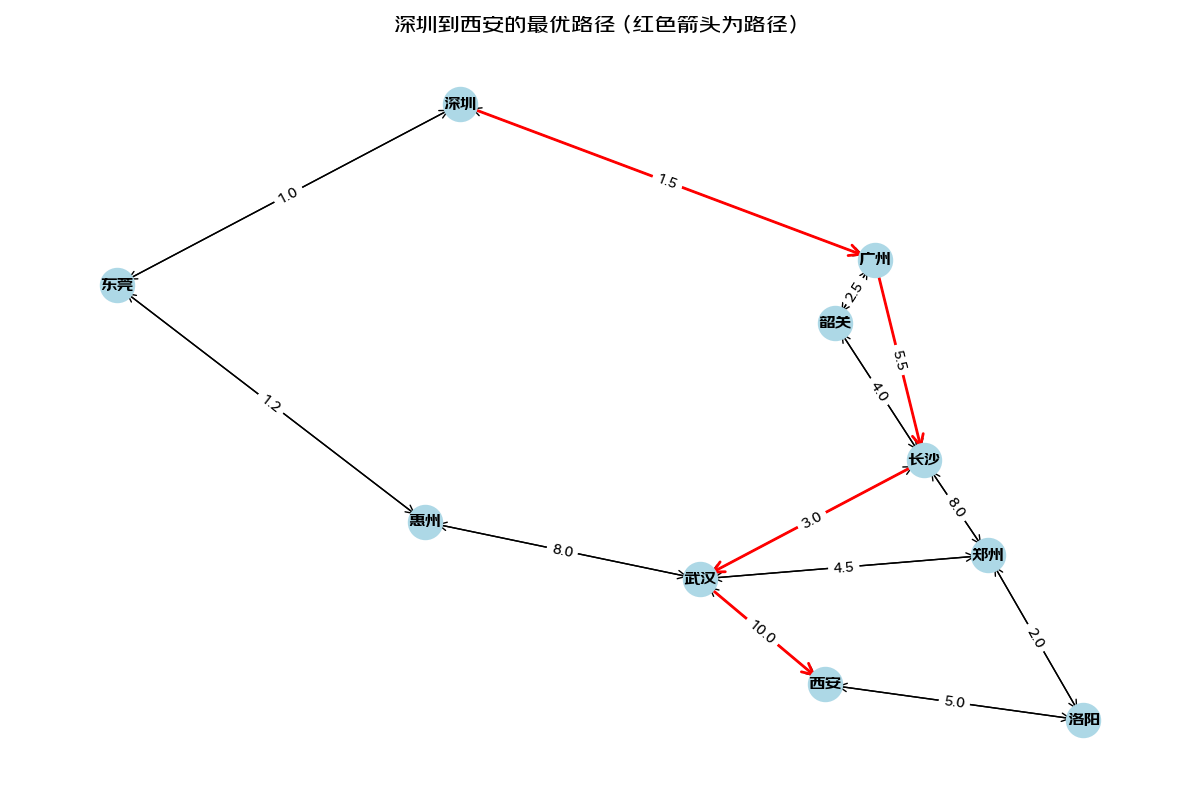
上面是只考虑最快的情况，加入费用因素就更好玩了

你有没有遇到过这种情况：比如你要从深圳去西安，有两条路线可选：

一条是坐高铁，虽然贵点，但快；
一条是坐大巴，便宜，但慢。

这时候你就会纠结了：到底是省时间重要，还是省钱更重要？

在我们之前的程序里，我们只考虑了运输时间，也就是“找出最快”的那条路。但现在我们要加一个新维度：运输费用 。这样我们可以让算法帮我们选出不同的方案，比如：

最便宜的路线；
最快的路线；
或者折中一点的路线 —— 时间不是最长，价格也不是最贵。

听起来是不是更贴近现实了？那怎么实现呢？

先给城市图加上“费用”

之前我们的 city_graph 是这样的：

'深圳': {'广州': 1.5, '东莞': 1.0}

现在我们把它改造成一个嵌套字典，每段路线都带两个属性：时间和费用：

'深圳': {'广州': {'time': 1.5, 'cost': 100}, '东莞': {'time': 1.0, 'cost': 60}}

这样，每个城市之间的连接就同时包含运输时间和运输成本了。

然后，我们想怎么权衡这两个因素？

你可以根据自己的需求设置权重，比如：

如果你赶时间，可以把时间的权重设得高一些；
如果你想省钱，就把费用的权重调高；
想要平衡的话，可以各占一半。

举个例子，假设我们定义一个公式：

combined_cost = alpha * time + beta * cost

其中：

alpha 和 beta 是你自己设定的权重，比如说 alpha=0.5, beta=0.5 就表示两者同等重要；
这样一来，每一段路线就有了一个“综合成本”，我们就可以在这个基础上运行 Dijkstra 算法来找最小的综合成本

改一下 Dijkstra 算法

原来的 Dijkstra 是找最短时间，现在我们要让它根据 combined_cost 来找最优路径。

修改后的核心逻辑大概是这样的：

for neighbor, attrs in graph[current_node].items():
    combined = alpha * attrs['time'] + beta * attrs['cost']
    distance = current_distance + combined

也就是说，我们不是直接加时间，而是加一个综合分数。

完整代码

import heapq

def dijkstra_with_combined_cost(graph, start, end, alpha=0.5, beta=0.5):
    distances = {node: float('inf') for node in graph}
    previous_nodes = {node: None for node in graph}
    distances[start] = 0

    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_node = heapq.heappop(priority_queue)

        if current_distance > distances[current_node]:
            continue

        for neighbor, attrs in graph[current_node].items():
            # 计算综合成本
            combined = alpha * attrs['time'] + beta * attrs['cost']
            new_distance = current_distance + combined

            if new_distance < distances[neighbor]:
                distances[neighbor] = new_distance
                previous_nodes[neighbor] = current_node
                heapq.heappush(priority_queue, (new_distance, neighbor))

    # 构建路径
    path = []
    node = end
    while node:
        path.append(node)
        node = previous_nodes[node]
    path.reverse()

    return distances[end], path

# 城市图（含时间和费用）
city_graph = {
    '深圳': {'广州': {'time': 1.5, 'cost': 100}, '东莞': {'time': 1.0, 'cost': 60}},
    '广州': {'深圳': {'time': 1.5, 'cost': 100}, '韶关': {'time': 2.5, 'cost': 120}, '长沙': {'time': 5.5, 'cost': 200}},
    '东莞': {'深圳': {'time': 1.0, 'cost': 60}, '惠州': {'time': 1.2, 'cost': 70}},
    '惠州': {'东莞': {'time': 1.2, 'cost': 70}, '武汉': {'time': 8.0, 'cost': 300}},
    '韶关': {'广州': {'time': 2.5, 'cost': 120}, '长沙': {'time': 4.0, 'cost': 180}},
    '长沙': {'韶关': {'time': 4.0, 'cost': 180}, '武汉': {'time': 3.0, 'cost': 150}, '郑州': {'time': 8.0, 'cost': 250}},
    '武汉': {'惠州': {'time': 8.0, 'cost': 300}, '长沙': {'time': 3.0, 'cost': 150}, '郑州': {'time': 4.5, 'cost': 200}, '西安': {'time': 10.0, 'cost': 400}},
    '郑州': {'长沙': {'time': 8.0, 'cost': 250}, '武汉': {'time': 4.5, 'cost': 200}, '洛阳': {'time': 2.0, 'cost': 90}},
    '洛阳': {'郑州': {'time': 2.0, 'cost': 90}, '西安': {'time': 5.0, 'cost': 180}},
    '西安': {'武汉': {'time': 10.0, 'cost': 400}, '洛阳': {'time': 5.0, 'cost': 180}}
}

# 找出不同策略下的最优路径
strategies = {
    "最省时间": {"alpha": 1.0, "beta": 0.0},
    "最省钱": {"alpha": 0.0, "beta": 1.0},
    "时间金钱兼顾": {"alpha": 0.5, "beta": 0.5}
}

for name, weights in strategies.items():
    total_cost, path = dijkstra_with_combined_cost(city_graph, '深圳', '西安', **weights)
    print(f"【{name}】")
    print(f"总综合成本：{total_cost:.2f}")
    print(f"路径：{' → '.join(path)}\n")

运行结果

/Users/allen/PycharmProjects/myPythonCode/venv/bin/python /Users/allen/PycharmProjects/myPythonCode/2506/lizhi-fee.py 
【最省时间】
总综合成本：20.00
路径：深圳 → 广州 → 长沙 → 武汉 → 西安

【最省钱】
总综合成本：820.00
路径：深圳 → 广州 → 长沙 → 郑州 → 洛阳 → 西安

【时间金钱兼顾】
总综合成本：421.00
路径：深圳 → 广州 → 长沙 → 郑州 → 洛阳 → 西安

Process finished with exit code 0

关于断路，移除城市之间的边就可以了，思路和最快路线一致。大家看到这里顶一下呀，

print("点赞+评论+收藏 = 以后吃的荔枝都新鲜！")

原创声明：本文系作者授权腾讯云开发者社区发表，未经许可，不得转载。

如有侵权，请联系 cloudcommunity@tencent.com 删除。

python

dijkstra

算法

热点技术征文第11期长安的荔枝

原创声明：本文系作者授权腾讯云开发者社区发表，未经许可，不得转载。

如有侵权，请联系 cloudcommunity@tencent.com 删除。

登录后参与评论

0 条评论

热度