【leetcode】解决递归问题的起点——相信自己写的函数头，一定能完成任务^ _ ^

📚️1. 理解递归

1.1什么是递归

简单来说就是函数自己调用自己（数据结构：二叉树，或者是快排以及我们的归并排序）

并且我们所了解的链表其实也是树形的一种，之不过就是只有一条分支

1.2为什么要使用递归

二叉树的遍历

快排：（边分边排序）

归并：基本思想（一直分，然后合并排序）

所以：出现了相同的问题，对于某一个节点的操作是一致的

本质：解决主问题的时候-》出现了一个子问题-》又出现了一个相同子问题，所以此时就要使用我们的递归

1.3如何理解递归

1.递归展开得到细节图

2.二叉树中的题目来理解递归

但是在上面的来看，一个递归函数例如二叉树，那是成倍数增长的，如果真的每次做递归的题目的时候，都要理解我们的递归的细节，那么就太夸张了~~~

3.宏观看待递归问题

不在意递归展开的细节展开图 把递归函数当成一个黑盒 相信黑盒一定能完成这个任务

是不是很奇怪，为啥相信我们的黑盒就可以完成任务；

举个例子：我们在进行二叉树的后序遍历的时候，我们可以规定，给定一个根结点，然后打印，所以这就是一个黑盒，那么传入左边和节点以及右边的节点就可打印，最后在完成打印printf即可；

所以代码就是很简短：

public void postOrder1(TreeNode root){
        if(root==null){
            return ;
        }
        postOrder1(root.left);
        postOrder1(root.right);
        System.out.println(root.val);
    }

这里的黑盒就是我们递归函数头，它的任务就是：给一个节点，帮我打印；

1.4如何写好一个递归

1.先找到相同的子问题-》决定函数头的设计

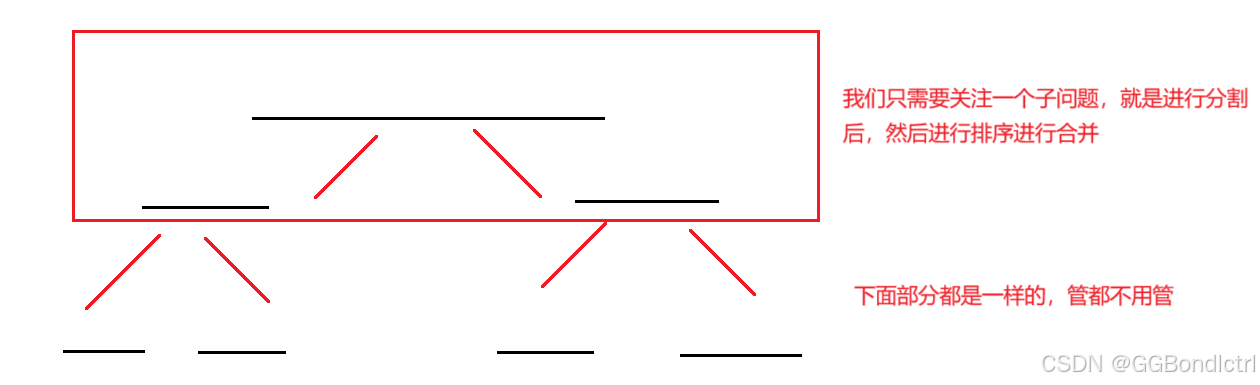
2.只关心某一个子问题是如何进行解决的（例如归并排序：找中间点，然后分成两半进行排序，然后合并即可）

3.出口问题，防止出现死循环

三个要素： 函数头 函数体 出口

例如我们的归并排序的函数体的设计：

📚️2.汉诺塔

2.1题目描述

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制: (1) 每次只能移动一个盘子; (2) 盘子只能从柱子顶端滑出移到下一根柱子; (3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

其实大家应该都应该了解过，假如有三个盘子要转移到我们的C柱上，如下：

2.2题目分析

那么我们进行分析：

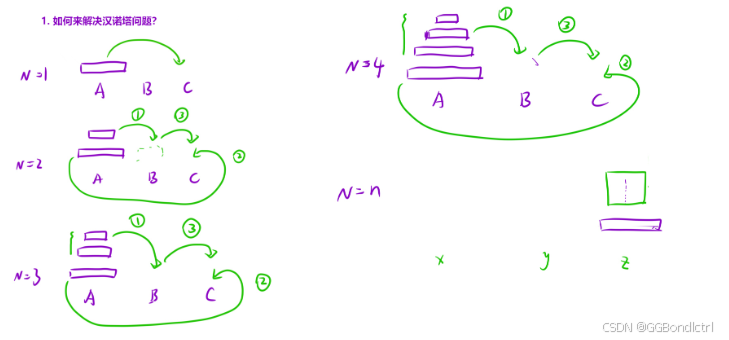
可以发现，我们在不管时N等于几时，都已看到，我们的目的是将我们的最大的那个盘放到C上，所以这里的重复的部分就是：

将A柱上的N-1个盘子放到我们的B上（借助我们的C）然后，将最大的那个盘放到我们的C柱上，然后将B上的盘子放到我们的C柱子上（借助我们的A盘）

所以我们的函数头就是dfs（x,y,z,n）将我们的N个盘子借助y转移到z上上面

2.3代码编写

class Solution {
    public void hanota(List<Integer> a, List<Integer> b, List<Integer> c) {
        dfs(a,b,c,a.size());
    }
    public void dfs(List<Integer> a, List<Integer> b, List<Integer> c,int n){
        //出口
        if(n == 1){
            c.add(a.remove(a.size() - 1));
            return;
        }
        dfs(a,c,b,n-1);
        c.add(a.remove(a.size() - 1));
        dfs(b,a,c,n-1);
    }
}

我们在dfs中首先要注意，当我们的n == 1时，就是我们的出口，只要把我们的a上面的盘子转移到c上，然后第一个dfs就是将a上面的n-1个盘子通过c辅助转移到b上面，然后将最后一个盘子转移到c上，以及最后一个dfs就是将b通过a的辅助转移到我们c上，后面就是我们转移盘子的数量

📚️3.合并两个有序链表

3.1题目描述

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

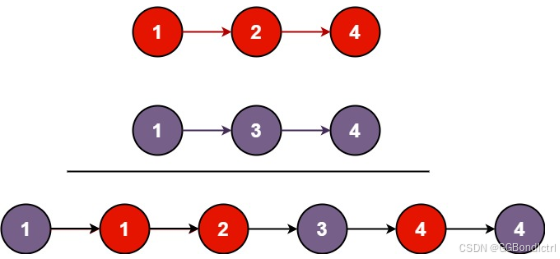
3.2题目分析

具体思路就是，函数头是什么，函数体的编写，函数的出口

首先我们看看函数头：

本题就是给两个链表，然后返回比较后的头节点

那么函数体就是：

在给两个链表返回头节点后，假如第一个l1链表的值更小，那么指向的就是两个链表返回的下一个比较小的头结点

出口就是当我们的头结点为空，或者下一个为空就返回；

3.3代码编写

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if(l1 == null){
            return l2;
        }
        if(l2 == null){
            return l1;
        }

        
        if(l1.val < l2.val){
            l1.next = mergeTwoLists(l1.next,l2);
            return l1;
        }else{
            l2.next = mergeTwoLists(l1,l2.next);
            return l2;
        }
    }
}

其实可以看成如下图示：

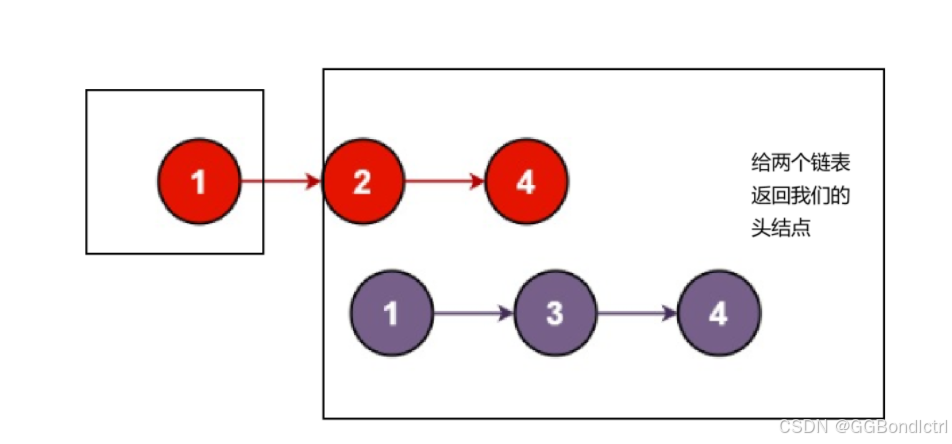
📚️4.翻转链表

4.1题目描述

给定单链表的头节点 head ，请反转链表，并返回反转后的链表的头节点。

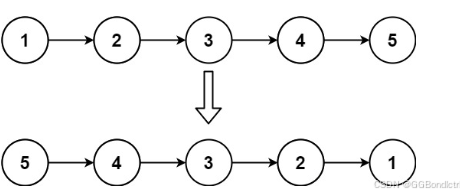
相信大家不用说都已经了解了吧

4.2题目分析

首先确定我们的函数头：

给一个头结点，然后返回我们逆置后的头结点

如下所示：

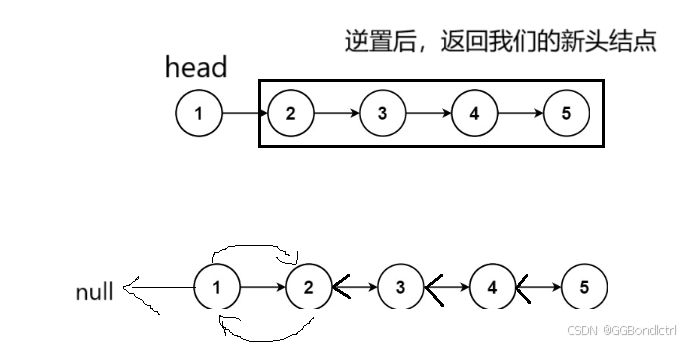
函数体就是在我们返回新的头结点后，将我们的head的next，next指向自己，然后head.next = null即可

4.3代码编写

class Solution {
    public ListNode reverseList(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
        ListNode newHead =  reverseList(head.next);
        head.next.next = head;
        head.next = null;

        return newHead;
    }
}

当然这里出口就是在head为空，那么就没有必要进行逆置操作了

📚️5.总结

这篇文章讲解了递归算法及其在力扣题目中的应用。首先介绍了递归的基本概念、使用场景（如二叉树遍历、排序算法）和理解方法（宏观看待递归）。然后通过三个经典题目详细解析：汉诺塔问题（借助中间柱转移盘子）、合并有序链表（比较节点值递归合并）和反转链表（修改指针指向递归翻转）。每个题目都分析了函数头设计、函数体逻辑和递归终止条件，并给出了对应的Java代码实现。文章强调理解递归的关键在于发现重复子问题并信任递归"黑盒"的能力，为学习递归提供了清晰的方法论。