编译原理 期末速成

一、基本概念

1. 翻译程序 vs 编译程序

翻译程序的三种方式

1. 编译：将高级语言编写的源程序翻译成等价的机器语言或汇编语言。（生成文件，等价）
2. 解释：将高级语言编写的源程序翻译一句执行一句，不生成目标文件，直接执行源代码文件。（一句一句，不生成为文件）
3. 汇编：用汇编语言编写的源程序翻译成与之等价的机器语言。

编译程序的五个阶段

1. 词法分析：对源程序的字符串进行扫描和分解，识别出每个单词符号。
2. 语法分析：根据语言的语法规则，把单词符号分解成各类语法单位。
3. 语义分析与中间代码生成：对各种语法范畴进行静态语义检查，若正确则进行中间代码翻译。
4. 代码优化：遵循程序的等价变换规则。
5. 目标代码生成：将中间代码变换成特定机器上的低级语言代码。

问题：源代码中括号不匹配的错误一般在编译的哪个阶段（采用五阶段划分模型）被检查出来，简述这一阶段的名称和主要任务

• 名称：语法分析
• 主要任务：读取词法符号，进行语法分析，判断源程序是否符合程序语法，并生成抽象语法树或语法符号

2. 上下文无关文法

标准格式（

）

：非空有限集，每个元素都是终结符

：非空有限集，每个元素都是非终结符

：非终极符号，即 开始符号

：产生式集合（有限），每个产生式的形式是

，其中

，

如果 G 是一个文法，S 为开始符号，如果

，则称

为一个 句型。仅含 终结符的句型是一个句子。文法 G 所产生的句子的全体是一个语言，记为 L(G)

3. 语法分析树

编译原理笔记9：语法分析树、语法树、二义性的消除

语法分析树是语言推导过程的图形化表示方法。这种表示方法反映了语言的实质以及语言的推导过程。

定义：对于 CFG G 的句型，分析树被定义为具有下述性质的一棵树：

1. 根由开始符号所标记；
2. 每个叶子由一个终结符、非终结符或 ε 标记；
3. 每个内部节点都是非终结符；
4. 若 A 是某节点的内部标记，且

是该节点从左到右的所有孩子的标记。则：

是一个产生式。若 A→ε，则标记为 A 的节点可以仅有一个标记为 ε 的孩子。

以 E => -E => -(E) => -(E+E) => -(id+E) => -(id+id) 为例

分析树与语言和文法的关系

• 每一直接推导（每个产生式），对应一仅有父子关系的子树，即产生式左部非终结符“长出”右部的孩子；
• 分析树的叶子，从左到右构成 CFG G 的一个句型（T、N两掺的串）。若叶子仅由终结符标记（+ 、- 、* 之类的运算符号也算是终结符），则构成一个句子

短语：子树末端节点字符串相对于子树根，即 叶子

简单短语（直接短语）：相当于简单子树

句柄：最左简单子树的末端节点组成字符串

• 注意：句柄这个概念有且仅会出现在 最右推导中

二义性：一个文法中存在某个句子，有两个不同的最左（最右）推导，则称这个文法是二义的

4. 语言分类🧠

0型文法(短语文法,上下文无关文法)，每个产生式的左边

且至少含有一个非终结符号

1. 定义：若文法

中的每个产生式规则的形式为：

，其中

且至少含有一个非终结符号，而

，则G[Z]为0型文法

1. 特点：0型文法的能力相当于图灵机，识别能力最强

1型文法(上下文敏感文法)

定义：若文法

中的每个产生式规则的形式为：

，其中

，

，

，则G[Z]为1型文法

例如

S → aAB
AB → BA
BA → a

其中 AB → BA 这类规则长度不变，但左部是多个符号，所以是 上下文有关文法 （1型）

2型文法(上下文无关文法)

定义：若文法

中的每个产生式规则的形式为：

，其中

，

，则G[Z]为2型文法

特点：语法结构上下文无关，一般用于识别程序设计语言的语法结构

例如

S → aSb | ε

这是一个 上下文无关文法 （2型），因为它每个产生式的左部都是一个单独的非终结符

3型语言(正规文法)

种类：右线性文法、左线性文法 正则文法 左（右）线性文法

右线性文法：若文法

中的每个产生式规则的形式为：

或

，其中

，则 G[Z] 为右线性文法。（非终结部分永远在右部）

左线性文法：若文法

中的每个产生式规则的形式为：

或

，其中

，则G[Z]为左线性文法。（非终结部分永远在左部）

特点：作为定义程序设计语言规则的文法

正规语言：3型文法定义的语言

例如

A → a
A → aB
B → b

这类产生式符合右线性正规文法，属于 3型文法

📌 总结步骤：

1. 检查是否每个产生式左边是一个非终结符 → 是：2型或以下
2. 再检查右边是否只能是“一个终结符”或“一个终结符+一个非终结符”，并且方向一致（左线性或右线性）→ 是：3型
3. 如果某些产生式左边是多个符号，则可能是1型
4. 否则是0型

当我们判断一个文法属于哪一型时，我们要找它能归入的最严格类型 （也就是编号最大的那个类型）

🧠 乔姆斯基文法的层级关系（包含关系）

例题： 已知文法 G(S) 的产生式集为： S->bA，A-> aA|a，请判断这个文法属于乔姆斯基几型文法

第一步：检查是否符合 2型文法（上下文无关文法，CFG）

2型文法的定义：

• 所有产生式的左边必须是一个单独的非终结符 。

观察该文法：

• S → bA：左边是 S（一个非终结符）
• A → aA | a：左边是 A（一个非终结符）

✔️ 全部产生式的左边都是单个非终结符 ，所以这是一个上下文无关文法（CFG） ，即2型文法

第二步：是否属于更严格的 3型文法（正规文法，Regular Grammar）

3型文法要求：

• 所有产生式必须是以下形式之一：
  • 右线性：A → a 或 A → aB（一个非终结符变成一个终结符后跟一个非终结符）
  • 左线性：A → Ba 或 A → a

看看当前文法：

• S → bA ✔️ 符合右线性
• A → aA ✔️ 符合右线性
• A → a ✔️ 是终结符，也符合右线性

✔️ 所有产生式都满足右线性正规文法的要求

➡️ 所以这个文法不仅是 2型文法，而且还是 3型文法（正规文法），因此最终结论：该文法属于乔姆斯基的第 3 型文法（正规文法）

5. LL(1) 分析方法

First集（最左边可能出现的终结符）：设G[Z]=(VN，VT，P，Z)，α∈(VN∪VT)，符号串α的首符号集合的定义为：

，则规定

Follow集：设G[Z]=(VN，VT，P，Z)，A∈VN，非终结符号A的后继符号集合的定义为：

，则规定#∈First(A)。#为结束符

LL(1)文法定义（也是 LL(1) 文法的判断条件）

1. 文法不含左递（如果有左递归，必须消除后再继续判断是否为 LL(1)）
2. 每个非终结符的各个候选式的 FIRST 集互不相交：对某个非终结符A，若其对应的产生式规则为

，则

1. 如果有某个候选式能推出 ε（空串）：即 A → α 和 A → β，其中 β ⇒* ε（即 ε ∈ FIRST(β)）

6. 左递归

含有A→Aa形式产生式的文法称为是直接左递归的 （immediate left recursive）

• 直接左递归：如果一个文法中有一个非终结符A使得对某个串a存在一个推导

，那么这个文法就是直接左递归的

• 间接左递归：经过两步或两步以上推导产生的左递归称为是间接左递归的

左递归缺点：容易产生死循环

消除直接左递归规则

• 若某个文法中非终结符A的产生式规则是 直接左递归规则：A→Aα|β，其中

。其中

不以A打头，

• 则将A的产生式规则改写为：

。

是新增加的非中介符号

消除间接左递归：

例

将S的定义代入A-产生式，得：

消除A-产生式的直接左递归，得：

二、习题练习

1. 文法化简

1. 若一个非终结符不能推导出终结字符串，则该非终结符是无用的，删除所有包括该非终结符的产生式规则
2. 若一个符号不能出现在文法的任何句型中，则该符号是无用的，删除所有包括该符号的产生式规则

题目：

解：

（1）从 S 开始，将含有非终结符不能推导出终结字符串消除，比如 C，因此删除

（2）最后结果为：

2. NFA、DFA 确定化、最小化

正归式转 NFA 规则如下：

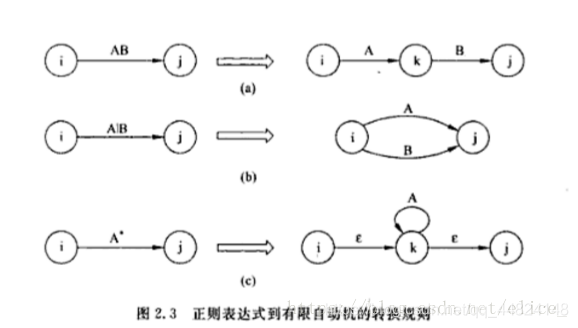
img

比如当前正则表达式为

，求其等价的 DFA

image-20250522154337328

NFA 确定化

要求确定化之前，需要判断是否有从该点出发的某个路径可以到达两个不同终点

题目如下：0 是终结 符号，求其 确定化，和 最小化的结果

graph LR;
	0 --> |a|0(((0)))
	0 ---> |a, b| 1((1));
	1 --> |a| 0;

• 注意：如果路径上有 ε，那么相当于无需任何条件可直接到达

由于 0 的 a 路径有两条，因此其并不是确定化，确定化状态转换矩阵如下：

{0}{0, 1}{1}{0, 1}{0, 1}{1}{1}{0}

• 注意：一般计算的时候也可以不考虑

先入 0 这个点到队列中，然后再把其通过 a, b 路径得到的值 依次入队列，然后按照 先进先出 的顺序取出，然后对 状态重新编号，如下：

012112203333

因此其 DFA 状态图为

graph LR;
	0(((0))) ---> |a|1((1))
	0 ---> |b|2((2))
	1--->|a|1
	1--->|b|2
	2--->|b|3((3))
	2--->|a|0
	3--->|a, b|3

其最小化求解如下：

包含最初的终结节点 0 的都属于 终态组，其他的就属于非终态组，比如：上面 DFA 确定化中 终态组{0, 1}，非终态组 {2，3}

由于 {0, 1} => {1}（a 路径下），{0，1} => {2}（b 路径下）

• 保证得到的状态集是属于当前集合的子集，就不用再分

因此终态组无需再分

然后再来看非终态组

由于 {2, 3} => {0，3}（a 路径下），{2，3} => {3}（b 路径下），前者不是当前集合子集，所以需要划分为 {2} {3}，故最小化的结果为 {0, 1}，{2}，{3}

然后再重新编号 ，最小化图为

graph LR;
	0 ---> |a|0(((0)))
	0--->|b|1((1))
	1--->|a|0
	1--->|b|2((2))
	2--->|a, b|2

3. 根据右线性文法求左线性文法

给定右线性文法 G：

画图得其 NFA 如下：

graph LR;
	0((S)) ---> |0,1|0(((0)))
	0 ---> |1|1((A)) 
	0 ---> |0|2((B))
	1 ---> |1|3((C)) 
	1 ---> |1|4((F))
	2 ---> |0|3
	2 ---> |0|4
	3 ---> |0,1|3
	3 ---> |0, 1|4

• 这里，S是起始状态，但是不是单纯的起点，它接收0或者1能够到达S状态。F是终止状态，是单纯的终点。

根据图，可以写出对应的左线性文法：

• F->A1|B0|C0|C1
• C->A1|B0|C0|C1
• B->S0（B是初始状态S接收0得到的，但是初始状态S并不是单纯的起点，它是状态S接收0/1得到的，所以需要写出来，如果写成B->0，是不对的，表达的不是一个意思，初始状态和终止状态写出来还是不写出来是严格确定的，如果写错，代表的是不同的自动机）
• A->S1
• S->S0|S1

4. 计算文法G的 FIRST 和 FOLLOW 集

文法 G 如下：

消除直接左递归结果如下：

如何求First集与Follow集（超详细） – 具体步骤在这

思路：

求 FIRST 集合：

1. 单个终结符 a

• 如果 X = a（a 是终结符），那么：FIRST(a)={a}

1. 空串 ε

• 如果 X = ε，那么：FIRST(ε)={ε}

1. 单个非终结符 A

• 对于每个非终结符 A，我们要看它所有的产生式右边的内容。
• 对于每一个 A → α 的产生式：
  • 把 FIRST(α) 中的元素加入到 FIRST(A) 中

FOLLOW 集合的构造规则

1. 初始化：
   • 如果 S 是文法的开始符号，则 # ∈ FOLLOW(S)，其中 # 表示输入结束符。
2. 基本规则：
   • 对于每一个产生式：

   A→αBβ

   其中：

   • A、B 是非终结符
   • α、β 是任意符号串（可以为空）

   则将 FIRST(β) 中除去 ε 的所有符号 加入到 FOLLOW(B) 中。

3. **ε 规则：**如果有产生式：

或

且 ε∈FIRST(β) 则将 FOLLOW(A) 中的所有符号加入到 FOLLOW(B) 中

1. **重复直到稳定：**因为 FOLLOW 集之间可能存在依赖关系，所以要反复应用上述规则，直到所有 FOLLOW 集不再变化为止

（，i），#

+，ε），#

（，i），+，#

*，ε），+，#

（，i*，），+，#